Offer必备算法33_DFS爆搜深搜回溯剪枝_八道力扣题详解（由易到难）

news2024/12/28 6:28:08

目录

①力扣784. 字母大小写全排列

解析代码1_path是全局变量

解析代码2_path是函数参数

②力扣526. 优美的排列

解析代码

③力扣51. N 皇后

解析代码

④力扣36. 有效的数独

解析代码

⑤力扣37. 解数独

解析代码

⑥力扣79. 单词搜索

解析代码

⑦力扣1219. 黄金矿工

解析代码

⑧力扣980. 不同路径 III

解析代码

本篇完。

①力扣784. 字母大小写全排列

784. 字母大小写全排列

难度 中等

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

  • 1 <= s.length <= 12
  • s 由小写英文字母、大写英文字母和数字组成
class Solution {
public:
    vector<string> letterCasePermutation(string s) {

    }
};

解析代码1_path是全局变量

只需要对英文字母进行处理，处理每个元素时存在三种情况：

  1. 不进行处理（字母也不处理，后面再处理，就是全部结果了）
  2. 若当前字母是英文字母并且是大写，将其修改为小写
  3. 若当前字母是英文字母并且是小写，将其修改为大写

path 是全局变量的代码：

class Solution {
    vector<string> ret;
    string path;
public:
    vector<string> letterCasePermutation(string s) {
        dfs(s, 0);
        return ret;
    }

    void dfs(const string& s, int pos)
    {
        if(path.size() == s.size())
        {
            ret.push_back(path);
            return;
        }
        char ch = s[pos];
        path.push_back(ch); // 不改变
        dfs(s, pos + 1);
        path.pop_back(); // 恢复现场

        if(ch < '0' || ch > '9') // 改变
        {
            path.push_back(change(ch)); // 改变
            dfs(s, pos + 1);
            path.pop_back(); // 恢复现场
        }
    }
    char change(char ch)
    {
        if(ch >= 'a' && ch <= 'z')
            ch -= 32;
        else
            ch += 32;
        return ch;
    }
};

解析代码2_path是函数参数

思路和解析代码1一样，path是函数参数的代码：

class Solution {
    vector<string> ret;
public:
    vector<string> letterCasePermutation(string s) {
        dfs(s, 0, "");
        return ret;
    }

    void dfs(const string& s, int pos, string path)
    {
        if(path.size() == s.size())
        {
            ret.push_back(path);
            return;
        }
        char ch = s[pos];
        dfs(s, pos + 1, path + ch); // 不改变

        if(ch < '0' || ch > '9') // 改变
        {
            dfs(s, pos + 1, path + change(ch));
        }
    }
    char change(char ch)
    {
        if(ch >= 'a' && ch <= 'z')
            ch -= 32;
        else
            ch += 32;
        return ch;
    }
};

②力扣526. 优美的排列

526. 优美的排列

难度 中等

假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件 之一 ，该数组就是一个 优美的排列 ：

  • perm[i] 能够被 i 整除
  • i 能够被 perm[i] 整除

给你一个整数 n ，返回可以构造的 优美排列 的 数量 。

示例 1：

输入：n = 2
输出：2
解释：
第 1 个优美的排列是 [1,2]：
    - perm[1] = 1 能被 i = 1 整除
    - perm[2] = 2 能被 i = 2 整除
第 2 个优美的排列是 [2,1]:
    - perm[1] = 2 能被 i = 1 整除
    - i = 2 能被 perm[2] = 1 整除

示例 2：

输入：n = 1
输出：1

提示：

  • 1 <= n <= 15
class Solution {
public:
    int countArrangement(int n) {

    }
};

解析代码

       题意是在每一个位置上考虑所有的可能情况并且不能出现重复。所以可以通过深度优先搜索的方式，不断地枚举每个数在当前位置的可能性，并回溯到上一个状态，直到枚举完所有可能性，得到正确的结果。

        需要定义一个变量用来记录所有可能的排列数量，一个一维数组 visited 标记元素，然后从第一个位置开始进行递归。递归函数作用：在当前位置填入一个合理的数字，查找所有满足条件的排列。

class Solution {
    bool vis[16];
    int ret;

public:
    int countArrangement(int n) {
        dfs(1, n);
        return ret;
    }

    void dfs(int pos, int n)
    {
        if(pos == n + 1) // 下标从1到n
        {
            ++ret;
            return;
        }
        
        for(int i = 1; i <= n; ++i)
        {
            if(!vis[i] && (pos % i == 0 || i % pos == 0))
            {
                vis[i] = true;
                dfs(pos + 1, n);
                vis[i] = false;
            }
        }
    }
};

③力扣51. N 皇后

51. N 皇后

难度 困难

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

  • 1 <= n <= 9
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {

    }
};

解析代码

        首先，我们在第一行放置第一个皇后，然后遍历棋盘的第二行，在可行的位置放置第二个皇后，然后再遍历第三行，在可行的位置放置第三个皇后，以此类推，直到放置了 n 个皇后为止。

       需要用一个数组来记录每一行放置的皇后的列数在每一行中，尝试放置一个皇后，并检查是否会和前面已经放置的皇后冲突。如果没有冲突，我们就继续递归地放置下一行的皇后，直到所有的皇后都放置完毕，然后把这个方案记录下来。

        在检查皇后是否冲突时，可以用一个数组来记录每一列是否已经放置了皇后，并检查当前要放置的皇后是否会和已经放置的皇后冲突。对于对角线，可以用两个数组来记录从左上角到右下角的每一条对角线上是否已经放置了皇后，以及从右上角到左下角的每一条对角线上是否已经放置了皇后。

对于对角线是否冲突的判断可以通过以下流程解决：（根据斜率相等得到 y = x + b 和 y = - x + b）

  • 从左上到右下：相同对角线的行列之差相同。（可能为负数，统一加上 n，y - x + n = b + n）
  • 从右上到左下：相同对角线的行列之和相同。（y + x = b）

        因此需要创建用于存储解决方案的二维字符串数组 solutions ，用于存储每个皇后的位置的一维整数数组 queens ，以及用于记录每一列和对角线上是否已经有皇后的布尔型数组checkCol、 checkDig1 和 checkDig2。

class Solution {
    vector<vector<string>> ret;
    vector<string> path;
    int _n;
    bool checkCol[10], checkDig1[20], checkDig2[20];

public:
    vector<vector<string>> solveNQueens(int n) {
        _n = n;
        path.resize(n);
        for(int i = 0; i < n; i++)
        {
            path[i].append(n, '.');
        }
        dfs(0);
        return ret;
    }

    void dfs(int row)
    {
        if(row == _n)
        {
            ret.push_back(path);
        }
        for(int col = 0; col < _n; ++col) // 枚举每一列，尝试在这⼀⾏放皇后
        {
            if(!checkCol[col] && !checkDig1[row - col + _n] && !checkDig2[row + col])
            {
                path[row][col] = 'Q';
                checkCol[col] = checkDig1[row - col + _n] = checkDig2[row + col] = true;
                dfs(row + 1);
                path[row][col] = '.'; // 恢复现场
                checkCol[col] = checkDig1[row - col + _n] = checkDig2[row + col] = false;
            }
        }
    }
};

④力扣36. 有效的数独

36. 有效的数独

难度 中等

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字（1-9）或者 '.'
class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {

    }
};

解析代码

此题不是DFS，相当于哈希，为了方便下一道DFS的剪枝。

创建三个数组标记行、列以及 3*3 小方格中是否出现 1~9 之间的数字即可：

        可以使用一个二维数组来记录每个数字在每一行中是否出现，一个二维数组来记录每个数字在每一列中是否出现。对于九宫格，可以用行和列除以 3 得到的商作为九宫格的坐标，并使用一个三维数组来记录每个数字在每一个九宫格中是否出现。在检查是否存在冲突时，只需检查行、列和九宫格里对应的数字是否已被标记。如果数字至少有一个位置（行、列、九宫格）被标记，则存在冲突，返回false。

class Solution {
        bool row[9][10];
        bool col[9][10];
        bool grid[3][3][10];

public:
    bool isValidSudoku(vector<vector<char>>& board) {
        for(int i = 0; i < 9; ++i)
        {
            for(int j = 0; j < 9; ++j)
            {
                if(board[i][j] != '.')
                {
                    int n = board[i][j] - '0';
                    if(row[i][n] || col[j][n] || grid[i / 3][j / 3][n])
                        return false;
                    row[i][n] = col[j][n] = grid[i / 3][j / 3][n] = true;
                }
            }
        }
        return true;
    }
};

⑤力扣37. 解数独

37. 解数独

难度 困难

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1：

输入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字或者 '.'
  • 题目数据 保证 输入数独仅有一个解
class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {

    }
};

解析代码

        为了存储每个位置的元素，我们需要定义⼀个⼆维数组。首先记录所有已知的数据，然后遍历所有需要处理的位置，并遍历数字 1~9。对于每个位置，检查该数字是否可以存放在该位置，同时检查行、列和九宫格是否唯一。

        根据力扣36. 有效的数独的解法，可以使用一个二维数组来记录每个数字在每一行中是否出现，一个二维数组来记录每个数字在每一列中是否出现。对于九宫格，可以用行和列除以 3 得到的商作为九宫格的坐标，并使用一个三维数组来记录每个数字在每一个九宫格中是否出现。在检查是否存在冲突时，只需检查行、列和九宫格里对应的数字是否已被标记。如果数字至少有一个位置（行、列、九宫格）被标记，则存在冲突，因此不能在该位置放置当前数字。

        特别地，在本题中，我们需要直接修改给出的数组，因此在找到一种可行的方法时，应该停止递归，以防止正确的方法被覆盖。

初始化定义：

  1. 定义行、列、九宫格标记数组以及找到可行方法的标记变量，将它们初始化为 false。
  2. 定义一个数组来存储每个需要处理的位置。
  3. 将题目给出的所有元素的行、列以及九宫格坐标标记为 true。
  4. 将所有需要处理的位置存入数组。

递归流程如下：

  1. 结束条件：已经处理完所有需要处理的元素。如果找到了可行的解决方案，则将标记变量更新为true 并返回。
  2. 获取当前需要处理的元素的行列值。
  3. 遍历数字 1~9。如果当前数字可以填入当前位置，并且标记变量未被赋值为 true，则将当前位置的行、列以及九宫格坐标标记为 true，将当前数字赋值给 board 数组中的相应位置元素，然后对下一个位置进⾏递归。
  4. 递归结束时，撤回标记。
class Solution {
    bool row[9][10];
    bool col[9][10];
    bool grid[3][3][10];

public:
    void solveSudoku(vector<vector<char>>& board) {
        for(int i = 0; i < 9; ++i) // 初始化
        {
            for(int j = 0; j < 9; ++j)
            {
                if(board[i][j] != '.')
                {
                    int n = board[i][j] - '0';
                    row[i][n] = col[j][n] = grid[i / 3][j / 3][n] = true;
                }
            }
        }
        dfs(board);
    }

    bool dfs(vector<vector<char>>& board)
    {
        for(int i = 0; i < 9; ++i)
        {
            for(int j = 0; j < 9; ++j)
            {
                if(board[i][j] == '.')
                {
                    for(int n = 1; n <= 9; ++n)
                    {
                        if(!row[i][n] && !col[j][n] && !grid[i / 3][j / 3][n])
                        {
                            board[i][j] = n + '0'; // 填数
                            row[i][n] = col[j][n] = grid[i / 3][j / 3][n] = true;
                            if(dfs(board) == true) // 填对了，告诉上一层填对了
                                return true;
                            board[i][j] = '.'; // 回复现场
                            row[i][n] = col[j][n] = grid[i / 3][j / 3][n] = false;
                        }
                    }
                    return false; // 1到9都不行
                }
            }
        }
        return true; // 填完了
    }
};

⑥力扣79. 单词搜索

79. 单词搜索

难度 中等

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

  • m == board.length
  • n = board[i].length
  • 1 <= m, n <= 6
  • 1 <= word.length <= 15
  • board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {

    }
};

解析代码

        思路：需要假设每个位置的元素作为第一个字母，然后向相邻的四个方向进行递归，并且不能出现重复用同一个位置的元素。通过深度优先搜索的方式，不断地枚举相邻元素作为下一个字母出现的可能性，并在递归结束时回溯，直到枚举完所有可能性，得到正确的结果。

递归函数流程：

  1. 遍历每个位置，标记当前位置并将当前位置的字母作为首字母进行递归，并且在回溯时撤回标记。
  2. 在每个递归的状态中，我们维护一个步数 step，表示当前已经处理了几个字母。若当前位置的字母与字符串中的第 step 个字母不相等，则返回 false。若当前 step 的值与字符串长度相等，表示存在一种路径使得 word 成立，返回 true。
  3. 对当前位置的上下左右四个相邻位置进行递归，若递归结果为 true，则返回 true。
  4. 若相邻的四个位置的递归结果都为 false，则返回 false。

        特别地，如果使用将当前遍历到的字符赋值为空格，并在回溯时恢复为原来的字母的方法，则在递归时不会重复遍历当前元素，可达到不使用标记数组的目的。

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool vis[7][7];
    int m, n;

public:
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size(), n = board[0].size();
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(board[i][j] == word[0])
                {
                    vis[i][j] = true;
                    if(dfs(board, i, j, word, 1) == true)
                        return true;
                    vis[i][j] = false;
                }
            }
        }
        return false;
    }

    bool dfs(vector<vector<char>>& board, int i, int j, string& word, int pos)
    {   // pos是遍历到了word的第几个字符
        if(pos == word.size())
            return true;
        for(int k = 0; k < 4; ++k)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == word[pos] && !vis[x][y])
            {
                vis[x][y] = true;
                if(dfs(board, x, y, word, pos + 1) == true)
                    return true;
                vis[x][y] = false;
            }
        }
        return false;
    }
};

⑦力扣1219. 黄金矿工

1219. 黄金矿工

难度 中等

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

  • 每当矿工进入一个单元，就会收集该单元格中的所有黄金。
  • 矿工每次可以从当前位置向上下左右四个方向走。
  • 每个单元格只能被开采（进入）一次。
  • 不得开采（进入）黄金数目为 0 的单元格。
  • 矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例 1：

输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],
 [5,8,7],
 [0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],
 [2,0,6],
 [3,4,5],
 [0,3,0],
 [9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

提示：

  • 1 <= grid.length, grid[i].length <= 15
  • 0 <= grid[i][j] <= 100
  • 最多 25 个单元格中有黄金。
class Solution {
public:
    int getMaximumGold(vector<vector<int>>& grid) {

    }
};

解析代码

        思路：枚举矩阵中所有的位置当成起点，来一次深度优先遍历，统计出所有情况下能收集到的黄金数的最大值即可。

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool vis[25][25];
    int m, n, ret;

public:
    int getMaximumGold(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(grid[i][j] != 0)
                {
                    vis[i][j] = true;
                    dfs(grid, i, j, grid[i][j]);
                    vis[i][j] = false;
                }
            }
        }
        return ret;
    }

    void dfs(vector<vector<int>>& grid, int i, int j, int sum)
    {
        ret = max(ret, sum);
        for(int k = 0; k < 4; ++k)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != 0 && !vis[x][y])
            {
                vis[x][y] = true;
                dfs(grid, x, y, sum + grid[x][y]);
                vis[x][y] = false;
            }
        }
    }
};

⑧力扣980. 不同路径 III

980. 不同路径 III

难度 困难

在二维网格 grid 上，有 4 种类型的方格：

  • 1 表示起始方格。且只有一个起始方格。
  • 2 表示结束方格，且只有一个结束方格。
  • 0 表示我们可以走过的空方格。
  • -1 表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目。

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

提示：

  • 1 <= grid.length * grid[0].length <= 20
class Solution {
public:
    int uniquePathsIII(vector<vector<int>>& grid) {

    }
};

解析代码

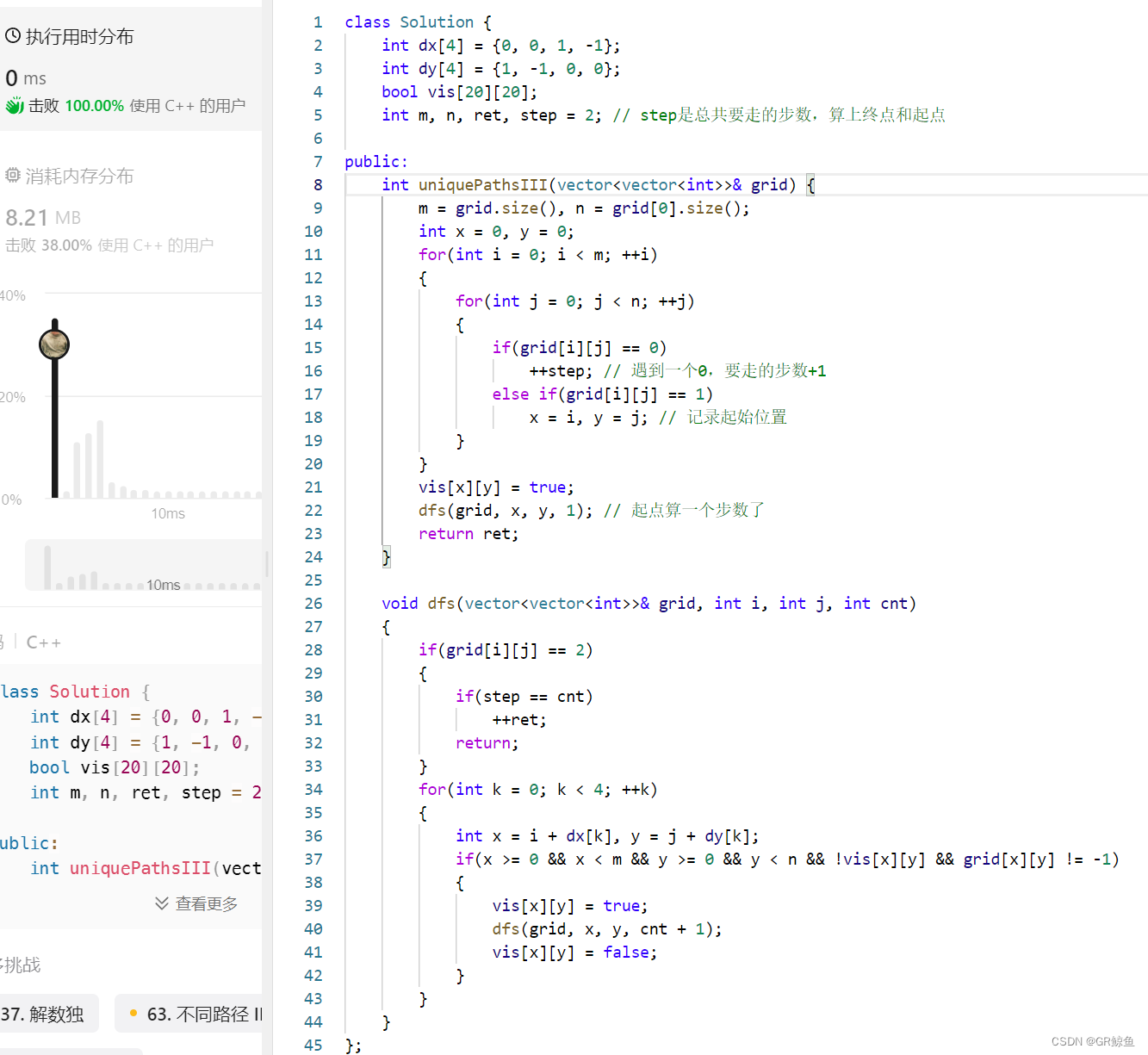
        可以用DP解决，但是这道题的DP是竞赛级别的，所以这里用爆搜的方法：题目要求到达目标位置时所有无障碍方格都存在路径中，我们可以定义一个变量记录 num 当前状态中剩余的未走过的无障碍方格个数，则当我们走到目标地点时只需要判断 num 是否 为 0 即可。在移动时需要判断是否越界。

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool vis[20][20];
    int m, n, ret, step = 2; // step是总共要走的步数，算上终点和起点

public:
    int uniquePathsIII(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        int x = 0, y = 0;
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                if(grid[i][j] == 0)
                    ++step; // 遇到一个0，要走的步数+1
                else if(grid[i][j] == 1)
                    x = i, y = j; // 记录起始位置
            }
        }
        vis[x][y] = true;
        dfs(grid, x, y, 1); // 起点算一个步数了
        return ret;
    }

    void dfs(vector<vector<int>>& grid, int i, int j, int cnt)
    {
        if(grid[i][j] == 2)
        {
            if(step == cnt)
                ++ret;
            return;
        }
        for(int k = 0; k < 4; ++k)
        {
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != -1 && !vis[x][y])
            {
                vis[x][y] = true;
                dfs(grid, x, y, cnt + 1);
                vis[x][y] = false;
            }
        }
    }
};

本篇完。

下一篇是贪心算法的第二部分，七八道题。

下下篇是DFS解决FloodFill类型的OJ。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1638584.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[嵌入式系统-58]：RT-Thread-内核：线程间通信，邮箱mailbox、消息队列MsgQueue、信号Signal

[嵌入式系统-58]：RT-Thread-内核：线程间通信，邮箱mailbox、消息队列MsgQueue、信号Signal

目录 线程间通信 1. 邮箱 1.1 邮箱的工作机制 1.2 邮箱控制块 1.3 邮箱的管理方式 &#xff08;1&#xff09;创建和删除邮箱 &#xff08;2&#xff09;初始化和脱离邮箱 &#xff08;3&#xff09;发送邮件 &#xff08;4&#xff09;等待方式发送邮件 &#xff08…
阅读更多...
excel 和 text 文件的读写操作

excel 和 text 文件的读写操作

excel 和 text 文件的读写操作 1. text 文件读写包 open语句 在文件存在的时候&#xff0c;即打开文件&#xff08;此时操作会覆盖文件&#xff0c;实际就是删除文件重后重新创建&#xff09;&#xff1b;在文件不存在的时候&#xff0c;即创建文件。 import sys print(sys.…
阅读更多...
商务谈判技巧与口才书籍有哪些类型

商务谈判技巧与口才书籍有哪些类型

商务谈判技巧与口才书籍有哪些类型&#xff08;3篇&#xff09; 商务谈判技巧与口才书籍的类型丰富多样&#xff0c;以下从三个角度进行介绍&#xff1a; **篇&#xff1a;基础理论与策略类书籍 这类书籍通常深入剖析谈判的本质&#xff0c;系统介绍谈判的原理、技巧和策略。…
阅读更多...
S-Clustr+Nets3e 僵尸网络偷拍照片插件

S-Clustr+Nets3e 僵尸网络偷拍照片插件

项目地址:https://github.com/MartinxMax/S-Clustr-Ring 更新内容 本次将Nets3e(https://github.com/MartinxMax/Nets3e/tree/Nets3e_V1.1.4)插件成功嵌入,意味着你可以指定任意节点下的主机进行拍照 一些嵌入式设备与工业PLC设备与个人PC计算机回连控制 核心服务端搭建 最好…
阅读更多...
MySQL-----多表查询（二）

MySQL-----多表查询（二）

目录 一.子查询概述&#xff1a; 二&#xff1a;标量子查询&#xff1a; 三&#xff1a;列子查询&#xff1a; 四&#xff1a;行子查询&#xff1a; 五&#xff1a;表子查询&#xff1a; 六&#xff1a;练习部分&#xff1a; 写在之前&#xff1a;本文承接上文MySQL-----多…
阅读更多...
邦注科技 温控箱对企业的重要性

邦注科技 温控箱对企业的重要性

注塑加工是将加热的熔融塑料注入模具中形成所需产品的工艺过程。良好的注塑加工工艺需要控制好许多参数&#xff0c;其中最重要的因素之一就是模具的温度。模具温度的不稳定会导致产品尺寸大小、表面缺陷等方面的问题&#xff0c;甚至会导致生产不良品&#xff0c;加大生产成本…
阅读更多...
普冉PY32系列(十五) PY32F0系列的低功耗模式

普冉PY32系列(十五) PY32F0系列的低功耗模式

目录 普冉PY32系列(一) PY32F0系列32位Cortex M0 MCU简介普冉PY32系列(二) Ubuntu GCC Toolchain和VSCode开发环境普冉PY32系列(三) PY32F002A资源实测 - 这个型号不简单普冉PY32系列(四) PY32F002A/003/030的时钟设置普冉PY32系列(五) 使用JLink RTT代替串口输出日志普冉PY32…
阅读更多...
【深入浅出MySQL】「性能调优」高性能查询优化MySQL的SQL语句编写

【深入浅出MySQL】「性能调优」高性能查询优化MySQL的SQL语句编写

高性能查询优化MySQL的SQL语句编写准则这里写目录标题 总体优化大纲&#xff08;1&#xff09;优化查询性能&#xff1a;通过索引降低全表扫描频率优化方向案例介绍问题分析解决方案建立复合索引建立单独索引 &#xff08;2&#xff09;优化数据表与查询&#xff1a;合理使用非…
阅读更多...
数组的扩容与缩容

数组的扩容与缩容

数组的扩容与缩容 文章目录 数组的扩容与缩容数组的扩容内存分析 数组的缩容内存分析内存分析 数组的扩容 数组扩容是指当原有数组的空间不足以容纳更多的元素时&#xff0c;创建一个新的、长度更大的数组&#xff0c;并将原数组中的元素复制到新数组中&#xff0c;然后更新原…
阅读更多...
OpenFeign夺命9连问

OpenFeign夺命9连问

今天介绍一款服务调用的组件&#xff1a;OpenFeign&#xff0c;同样是一款超越先辈&#xff08;Ribbon、Feign&#xff09;的狠角色。 文章目录如下&#xff1a; 这篇文章之前陈某发过&#xff0c;全网阅读 10W &#xff0c;时隔一年发出来让大家复习复习&#xff0c;部分读者…
阅读更多...
LNMP部署及应用（Linux+Nginx+MySQL+PHP)

LNMP部署及应用（Linux+Nginx+MySQL+PHP)

LNMP 我们为什么采用LNMP这种架构? 采用Linux、PHP、MySQL的优点我们不必多说。 Nginx是一个小巧而高效的Linux下的Web服务器软件&#xff0c;是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的&#xff0c;已经在一些俄罗斯的大型网站上运行多年&#xff0c;目…
阅读更多...
Spring - 10 ( 9000 字 Spring 入门级教程 )

Spring - 10 ( 9000 字 Spring 入门级教程 )

一&#xff1a;MyBatis 进阶 动态 SQL 是 Mybatis 的强大特性之⼀&#xff0c;能够完成不同条件下不同的 sql 拼接。 1.1 if 标签 在注册用户的时候&#xff0c;可能会有这样⼀个问题&#xff0c;如下图所示&#xff1a; 注册分为两种字段&#xff1a;必填字段和非必填字段&…
阅读更多...
【二】电力系统规约IEC 104详解

【二】电力系统规约IEC 104详解

电力系统规约IEC 104详解 概述 很早就准备梳理出一下电力系统规约系列的文章&#xff0c;因为自己在实践过程中发现这方面太难找了&#xff0c;网上的资料也都比较陈旧。我接触和使用IEC系列规约也有一段时间了&#xff0c;本着总结和分享的想法&#xff0c;我想推出这系列的文…
阅读更多...
Linux的基础IO：文件描述符 重定向本质

Linux的基础IO：文件描述符 重定向本质

目录 前言 文件操作的系统调用接口 open函数 close函数 write函数 read函数 注意事项 文件描述符-fd 小补充 重定向 文件描述符的分配原则 系统调用接口-dup2 缓冲区 缓冲区的刷新策略 对于“2”的理解 小补充 前言 在Linux中一切皆文件&#xff0c;打开文件…
阅读更多...
Android 音视频基础知识

Android 音视频基础知识

本系列文章会介绍两个 Android NDK Demo&#xff0c;拉流端会实现一个基于 FFmpeg 的视频播放器 Demo&#xff0c;推流端会实现一个视频直播 Demo&#xff0c;当然在做 Demo 之前会介绍音视频的基础知识。以下是本系列文章的目录&#xff1a; Android 音视频基础知识 Android 音…
阅读更多...
SpringBoot集成Kafka开发

SpringBoot集成Kafka开发

4.SpringBoot集成Kafka开发 4.1 创建项目 4.2 配置文件 application.yml spring:application:name: spring-boot-01-kafka-basekafka:bootstrap-servers: 192.168.2.118:90924.3 创建生产者 package com.zzc.producer;import jakarta.annotation.Resource; import org.spri…
阅读更多...
HTML5本地存储账号密码

HTML5本地存储账号密码

<!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>HTML5本地存储账号密码</title> </head…
阅读更多...
C语言/数据结构——每日一题（合并两个有序链表）

C语言/数据结构——每日一题（合并两个有序链表）

一.前言 嗨嗨嗨&#xff0c;大家好久不见&#xff01;今天我在LeetCode看到了一道单链表题&#xff1a;https://leetcode.cn/problems/merge-two-sorted-lists想着和大家分享一下&#xff0c;废话不多说&#xff0c;让我们开始今天的题目分享吧。 二.正文 1.1题目描述 1.2题…
阅读更多...
2.2 Java全栈开发前端+后端（全栈工程师进阶之路）-前端框架VUE3-基础-Vue基本语法

2.2 Java全栈开发前端+后端（全栈工程师进阶之路）-前端框架VUE3-基础-Vue基本语法

文本渲染指令 文本渲染指令-v-html与v-text Vue使用了基于HTML的模板语法&#xff0c;允许开发者声明式地将DOM绑定至底层Vue实例的数据。所有Vue的模板都是 合法的HTML&#xff0c;所以能被遵循规范的浏览器和HTML解析器解析。 在前面&#xff0c;我们一直使用的是字符串插…
阅读更多...
利用STM32实现语音识别功能

利用STM32实现语音识别功能

引言 随着物联网和智能设备的普及&#xff0c;语音识别技术正逐渐成为用户交互的主流方式之一。 STM32微控制器具备处理高效率语音识别算法的能力&#xff0c;使其成为实现低成本、低功耗语音交互系统的理想选择。 本教程将介绍如何在STM32平台上开发和部署一个基础的语音识…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023