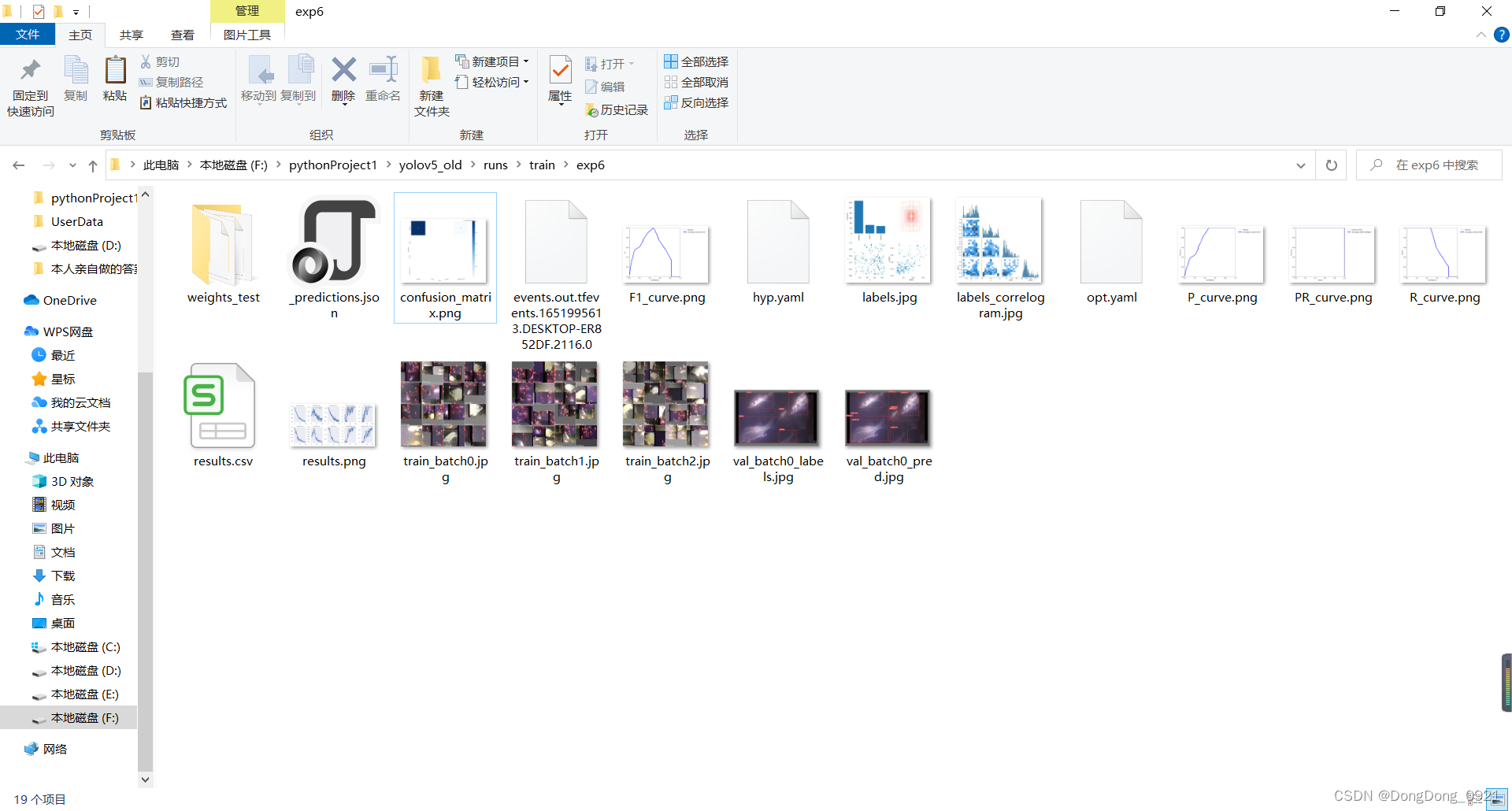
本文的目的是帮助理解每次训练后,在runs/train文件夹下出现的一系列文件,并探索如何评估准确率以及模型的好坏。
一.混淆矩阵—confusion_matrix.png
毕设跑的train有混淆矩阵,但是有点扯,需要跑一下鸟类的验证一下(待验证)
1.概念
混淆矩阵是对分类问题预测结果的总结。使用计数值汇总正确和不正确预测的数量,并按每个类进行细分,显示了分类模型进行预测时会对哪一部分产生混淆。
混淆矩阵不仅可以让我们直观的了解分类模型所犯的错误,更重要的是可以了解哪些错误类型正在发生,正是这种对结果的分解克服了仅使用分类准确率带来的局限性。
2.图文理解
| 实际 | ||||
| 类1 | 类2 | 类3 | ||
| 预测 | 类1 | 43 | 5 | 2 |
| 类2 | 2 | 45 | 3 | |
| 类3 | 0 | 1 | 49 | |
(1)横轴时预测类别,纵轴是真实类别;
(2)表格里的数目总数为150,表示共有150个测试样本;
(3)每一行之和为50,表示每类各有50个样本,每一行代表了真实的目标被预测为其他类的数量,比如第一行:43代表真实的类一中有43个被预测为类一,5个被错预测为类2,2个被错预测为类3;
二.TP/TN/FP/FN
1.逻辑关系
T(True):最终预测结果正确。
F(False):最后预测结果错误。
P(Positive):模型预测其是正例(目标本身是个鱼,模型也预测它是个鱼)。
N(Negative):模型预测其是负例(目标本身是个鱼,但模型预测它是个猫)。
TP:样本的真实类别是正例,并且模型预测的结果也是正例,预测正确(目标本身是个鱼,模型也预测它是鱼,预测正确;还有一种理解方式,模型预测它是正例,最终预测结果是正确的,所以目标是个正例))。
TN:样本的真实类别是负例,并且模型将其预测成为负例,预测正确(目标本身不是鱼,模型预测它不是了鱼,是个其他的东西,预测正确;还有一种理解方式,模型预测它是负例,最终预测结果是正确的,所以目标是个负例))。
FP:样本的真实类别是负例,但是模型将其预测成为正例,预测错误(目标本身不是鱼,模型预测它是鱼,预测错误;还有一种理解方式,模型预测它是正例,最终预测结果是错误的,所以目标是个负例)。
FN:样本的真实类别是正例,但是模型将其预测成为负例,预测错误(目标本身是鱼,模型预测它不是鱼,是个其他的东西,预测错误;还有一种理解方式,模型预测它是负例,最终预测结果是错误的,所以目标是个正例)。
2.几个指标
(1)正确率/准确率(accuracy)=;
注:通常来说正确率越高,模型越好。
(2)错误率=;
(3)灵敏度(sensitive)=;
注:表示的是所有正例中被分对的比例,衡量了分类器对正例的识别能力;
(4)特征度/特异度(specificity)=
注:表示的是所有负例中被分对的比例,衡量了分类器对负例的识别能力;
(5)精确率(precision)=
注:表示被分为正例的示例中实际为正例的比例;
(6)召回率(recall)=
注:度量有多个正例被分为正例;
3.label.jpg
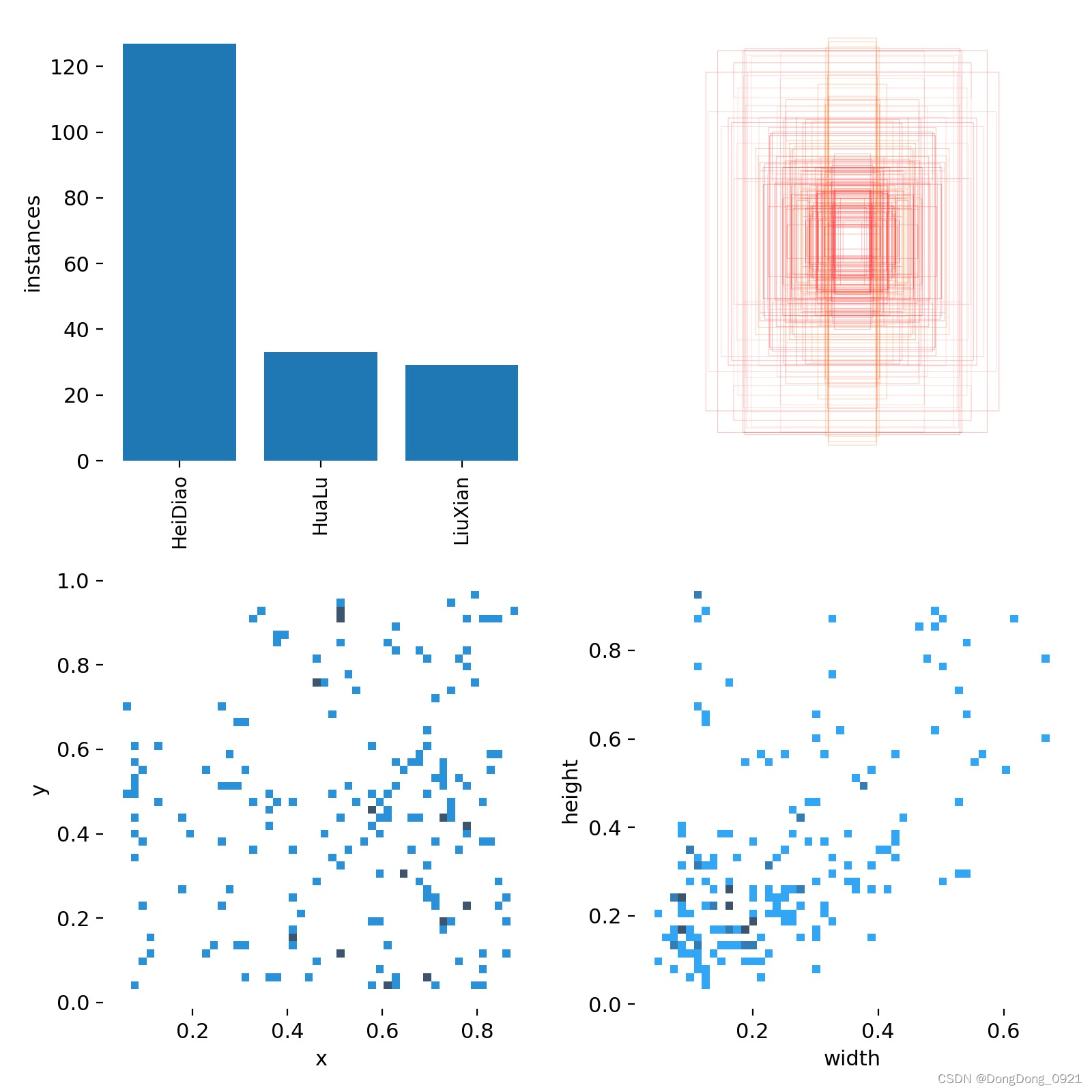
第一张图:classes(每个类别的数据量)
第二个图:labels(框的尺寸和数量)
第三个图:center (框的中心点坐标)
第四个图:labels width and height(框的长和宽)
4.P_curve(精确率和置信度的关系图)
精确率(查准率):表示被分为正例的示例中实际为正例的比例
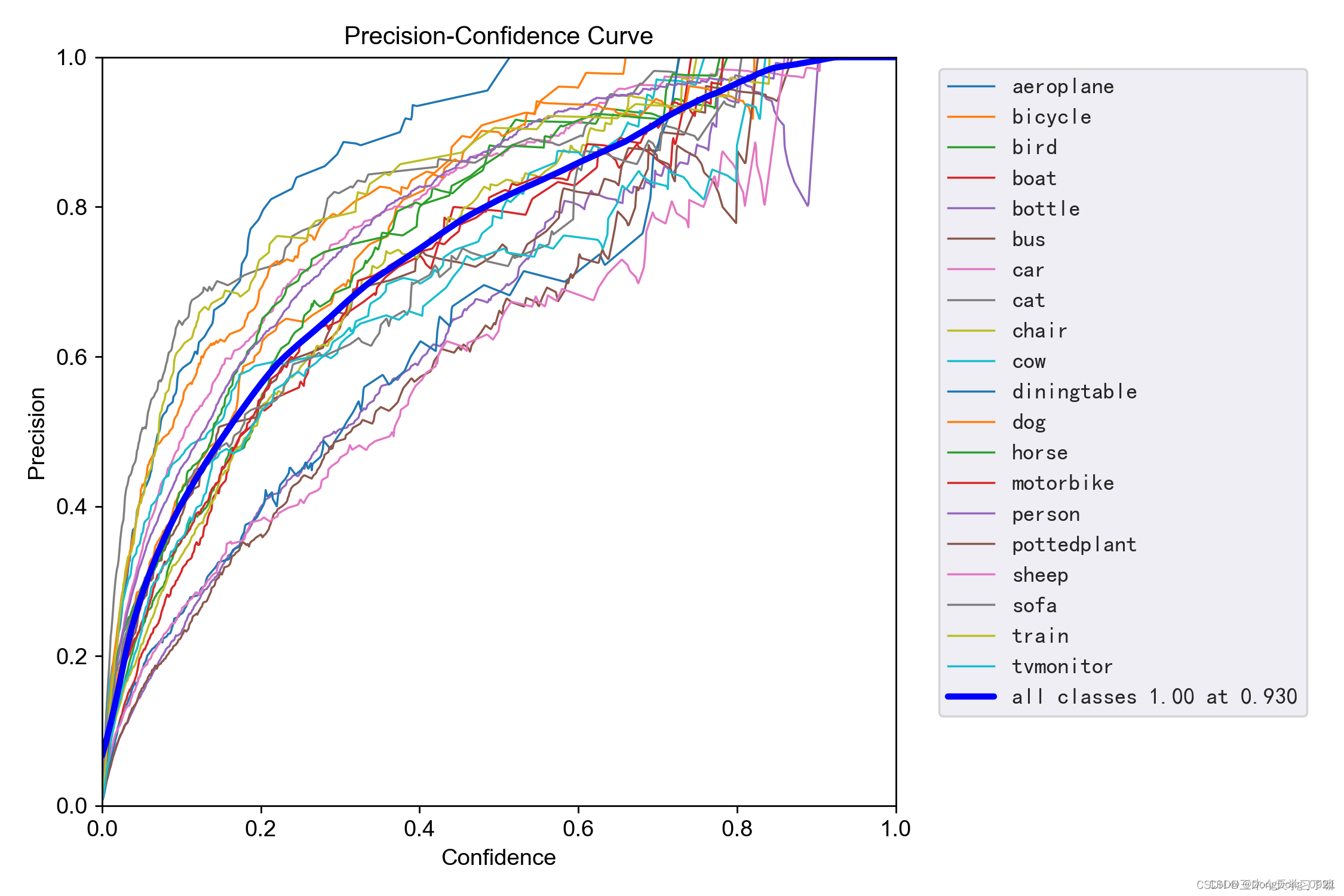
解释:设置置信度为某一数值的时候,各个类别识别的精确率。
可以看到,当置信度越大的时候,类别检测的越准确。这也很好理解,只有置信度很大,才被判断是某一类别。但这样的话,会漏检一些置信度低的类别。
比如运行程序时,即便某个目标是鱼,模型预测它也是鱼,但是给它的置信度只有70%,当置信度设置在80%时才认为是鱼时,这个目标就会被忽略了。
5.R_curve(召回率和置信度的关系图)
召回率(查全率):度量有多个正例被分为正例
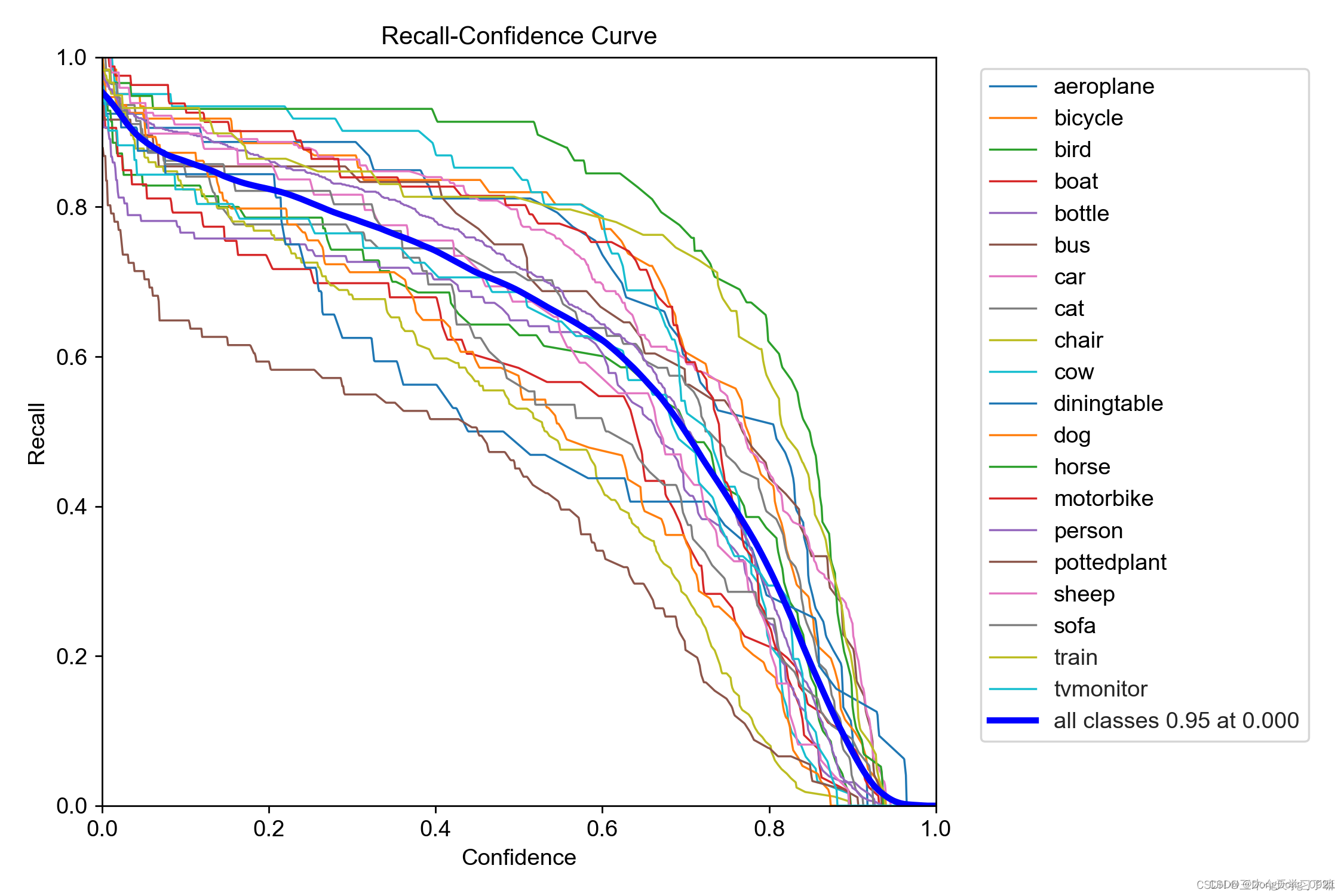
解释:设置置信度为某一数值的时候,各个类别查全的概率。可以看到,当置信度越小的时候,类别检测的越全面。
6.先验知识综合recall和precision
Precision和Recall通常是一对矛盾的性能度量指标。一般来说,Precision越高时,Recall往往越低。
原因是:如果我们希望提高Precision,即二分类器预测的正例尽可能是真实正例,那么就要提高二分类器预测正例的门槛。例如,之前预测正例只要置信度0.5的样例我们就标注为正例,那么现在要提高到置信度
0.7我们才标注为正例,这样才能保证二分类器挑选出来的正例更有可能是真实正例;而这个目标恰恰与提高Recall相反,如果我们希望提高Recall,即二分类器尽可能地将真实正例挑选出来,那么势必要降低二分类器预测正例的门槛,例如之前预测正例只要置信度
0.5的样例我们就标注为真实正例,那么现在要降低到
0.3我们就将其标注为正例,这样才能保证二分类器挑选出尽可能多的真实正例 。
注:算法会为每个目标分配一个置信度
对于二分类器,我的理解是:即便是有多个目标,因为在P_curve和R_curve中,每一类都有一条自己对应的曲线,所以在计算每一类的时候(比如鱼),鱼就是正例,其余的不管有多少类通通归为负例。
7.PR_curve(精确率和召回率的关系图)
mAP (Mean Average Precision),即均值平均精度。
mAP是所有类别AP的均值,AP由精确率和召回率确定;而IoU 阈值、confidence(置信度) 阈值影响精确率和召回率的计算。计算精确率和召回率时需要判断TP、FP、TN、FN
@后面的数表示判定iou为正负例的阈值
可以看到:精度越高,召回率越低。
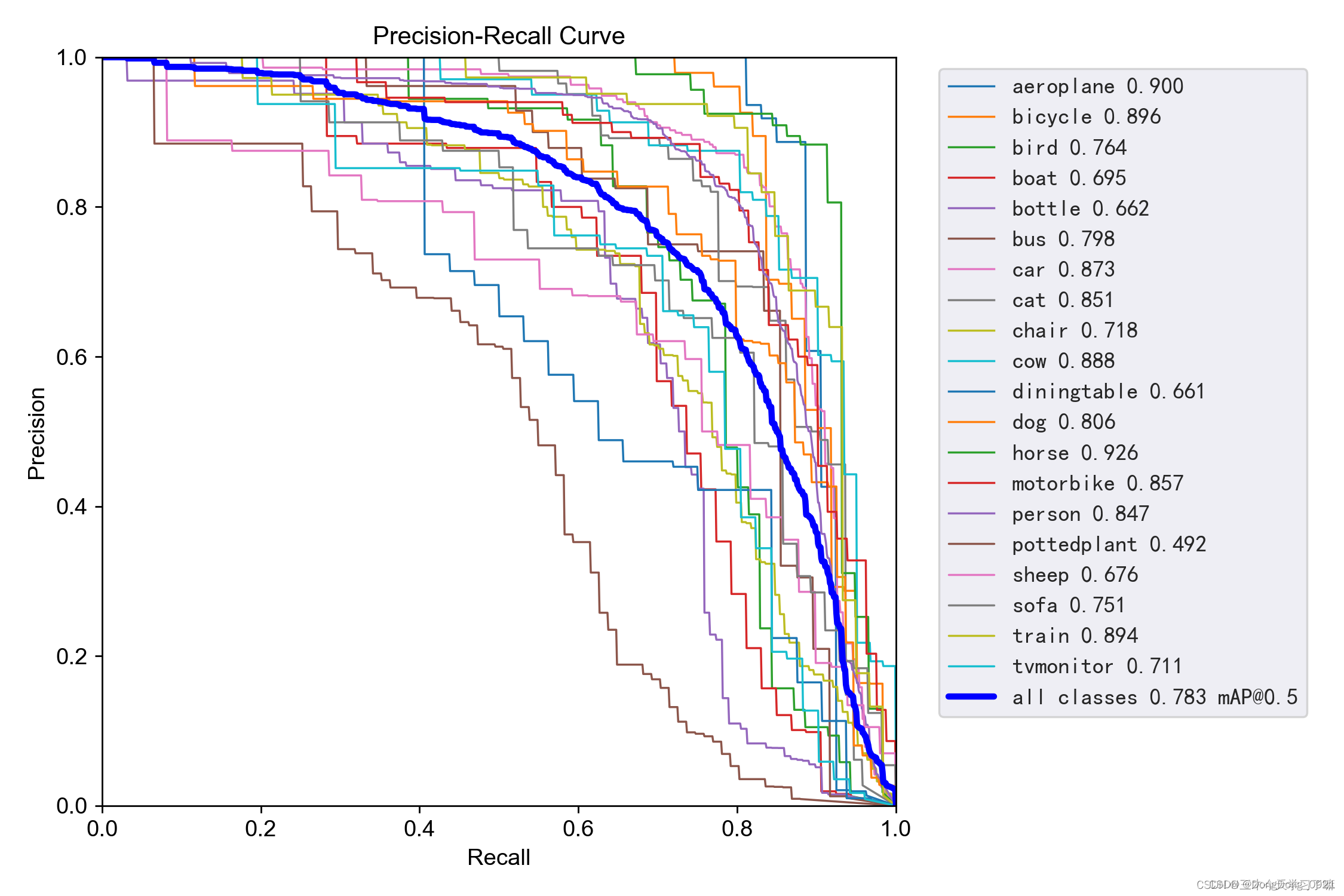
我们希望我们的网络,在准确率很高的前提下,尽可能的检测到全部的类别。所以希望我们的曲线接近(1,1)点,即希望mAP曲线的面积尽可能接近1。
第一个衡量指标:mAP曲线的面积大小。
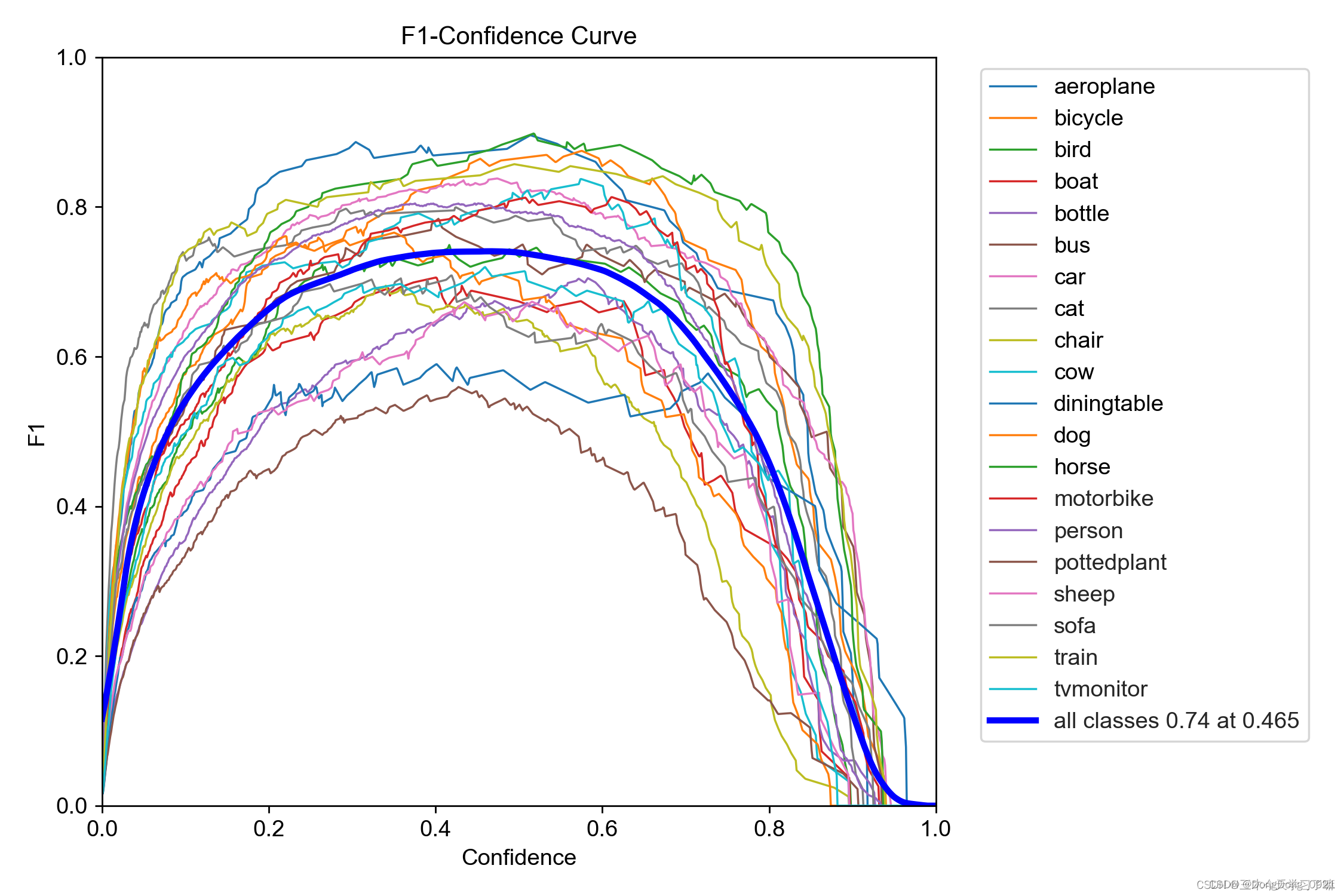
8.F1_curve
F1分数(F1-score)是分类问题的一个衡量指标。是精确率和召回率的调和平均数,1是最好,0是最差。
9.可视化训练结果解析
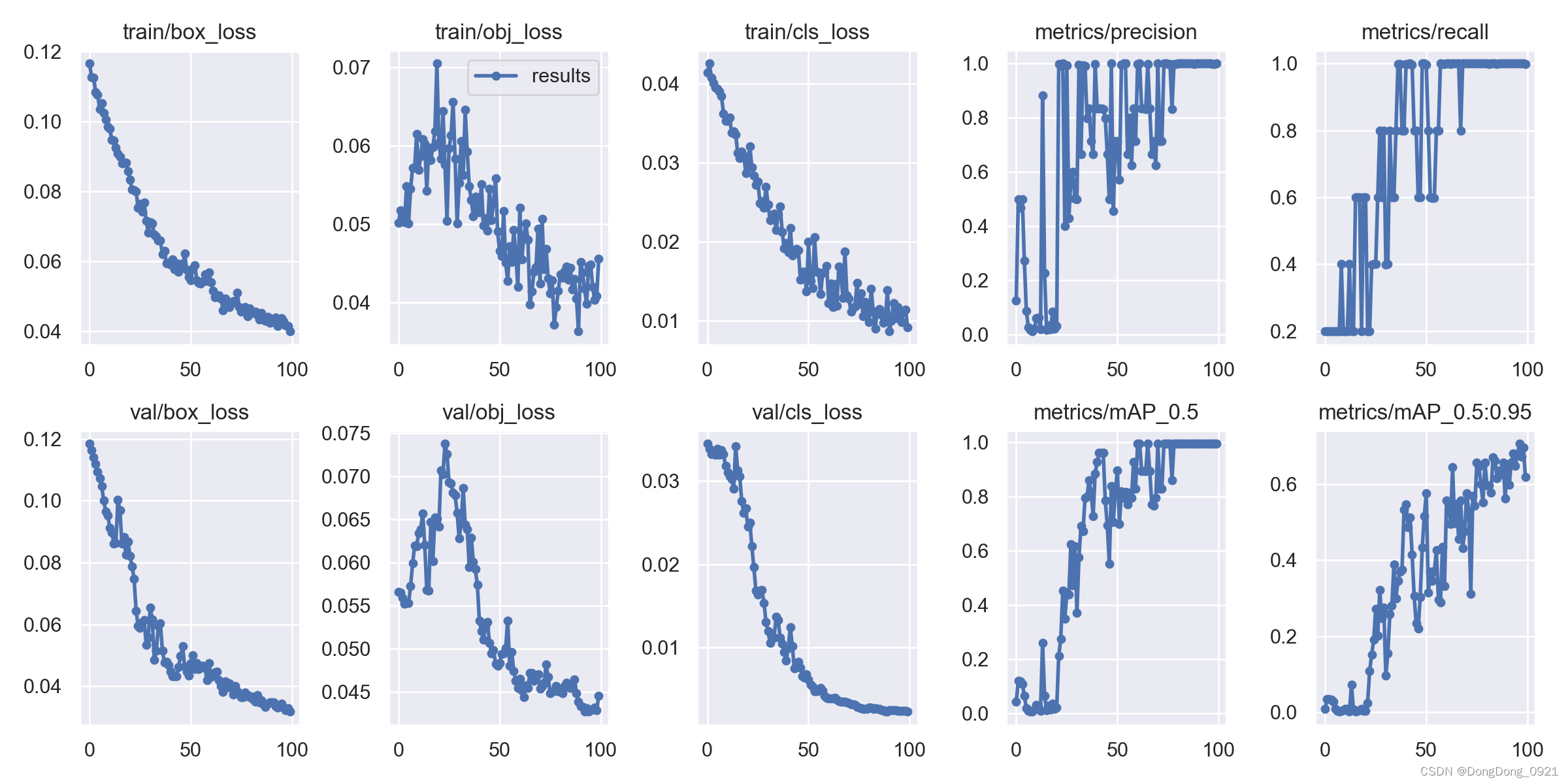
横坐标代表的是训练轮数(epoch)
obj(Objectness):推测为目标检测loss均值,越小目标检测越准。
cls(Classification):推测为分类loss均值,越小分类越准。
第二个衡量指标:宏观上一般训练结果主要观察精度和召回率波动情况,波动不是很大则训练效果较好;如果训练比较好的话图上呈现的是稳步上升。
10.小感悟
Q1:在学习YOLOv5训练结果分析的过程中突然有了一个疑问:train.py不就是训练训练图片,怎么会涉及到精确率的问题?
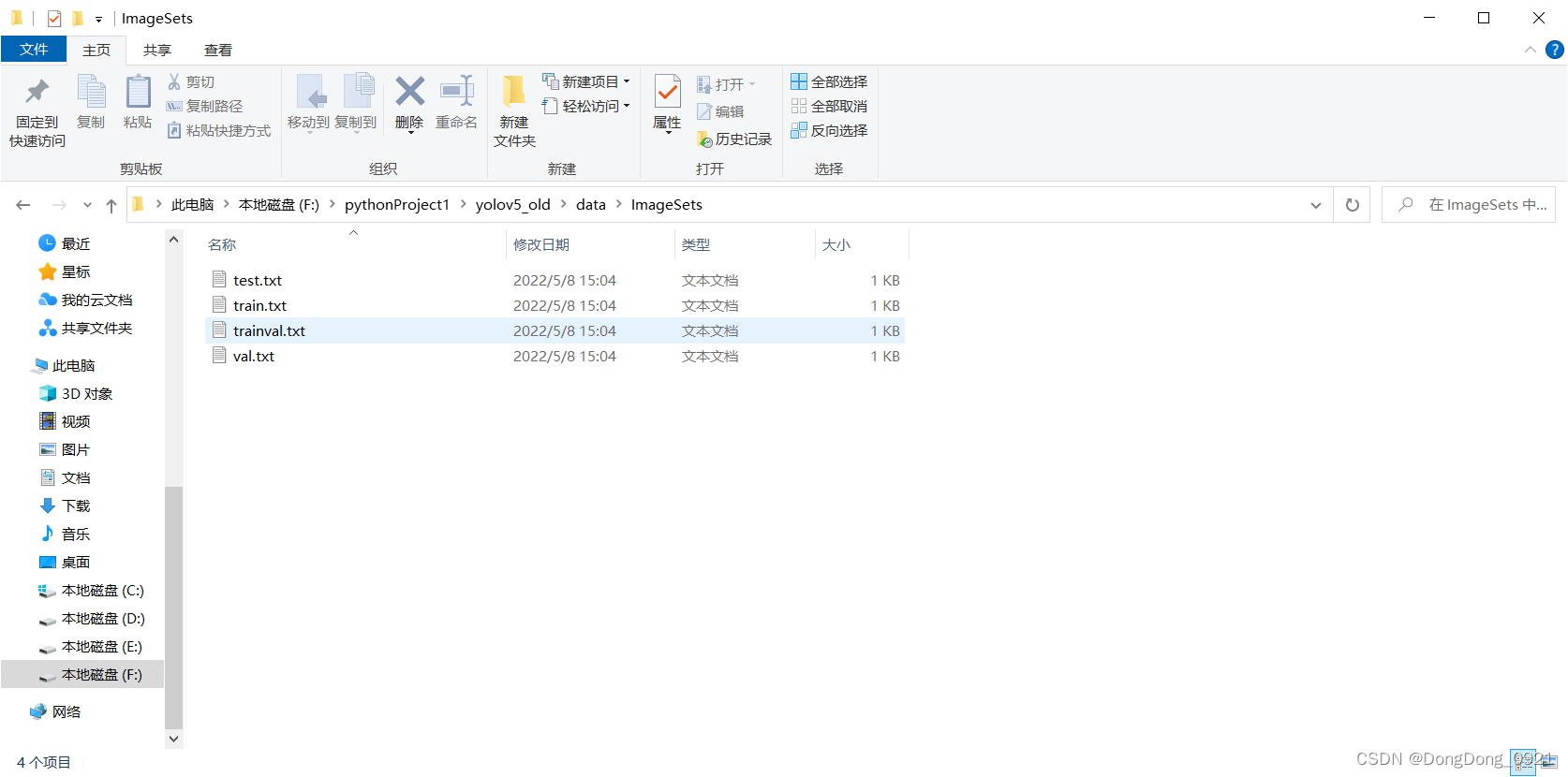
解释:在训练过程中,有一步会生成训练集(train.txt)、验证集(val.txt)、测试集(test.txt),其中存放图片的名字(无后缀.jpg)。
训练集:用于训练模型以及确定参数。相当于老师教学生知识的过程。
验证集:用于确定网络结构以及调整模型的超参数。相当于月考等小测验,用于学生对学习的查漏补缺。
测试集:用于检验模型的泛化能力。相当于大考,上战场一样,真正的去检验学生的学习效果。
所以我感觉正是测试测试集的过程中,才出来的精确率、召回率等参数。
关于毕设训练结果文档中P_curve、R_curve都只有黑鲷的原因是:测试集里只有黑鲷的图片。
这里设计到训练集、验证集、测试集的比例划分(未解决)
半成品:仅仅是为了自己理解YOLOv5的具体原理,如有侵权,麻烦告知,立删