在计算机科学领域,图搜索算法是一类用于在图数据结构中查找特定节点或路径的算法。图搜索算法在许多领域都有着广泛的应用,包括网络路由、社交网络分析、游戏开发等。本文将详细介绍几种常见的图搜索算法,包括深度优先搜索(DFS)、广度优先搜索(BFS),并提供Python示例代码。后面再介绍Dijkstra算法和A*算法。
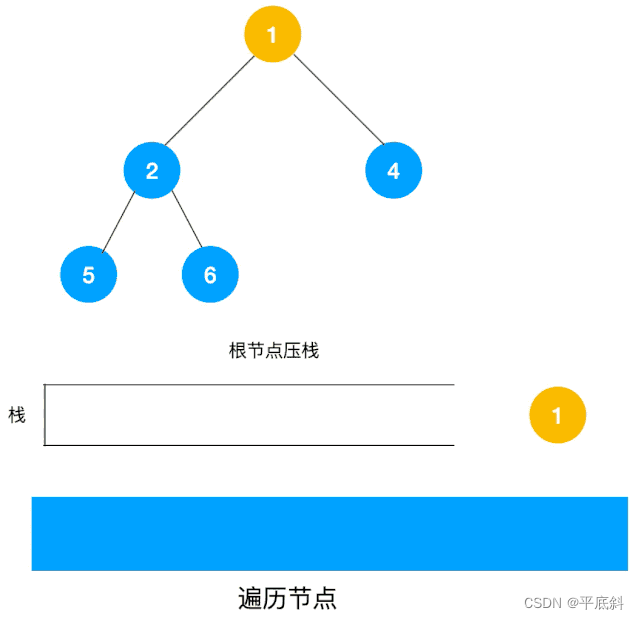
- 深度优先搜索(DFS)
深度优先搜索是一种经典的图搜索算法,它通过递归或栈来实现。DFS从起始节点开始,沿着一条路径一直向下搜索直到无法继续,然后回溯到前一个节点继续搜索。DFS常用于解决图中的连通性问题,如判断图是否连通、查找图中的环等。
from collections import defaultdict
class Graph:
def __init__(self):
self.graph = defaultdict(list)
def add_edge(self, u, v):
self.graph[u].append(v)
def dfs_util(self, v, visited, target, path):
visited[v] = True
path.append(v)
if v == target:
print("DFS Path:", path)
else:
for i in self.graph[v]:
if not visited[i]:
self.dfs_util(i, visited, target, path)
path.pop()
visited[v] = False
def dfs(self, start, target):
visited = [False] * (max(self.graph) + 1)
path = []
self.dfs_util(start, visited, target, path)
# 创建图实例
g = Graph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)
start_node = 2
target_node = 3
print("Starting from node", start_node)
print("Searching for node", target_node)
# 使用DFS算法搜索路径
g.dfs(start_node, target_node)
- 广度优先搜索(BFS)
广度优先搜索是另一种常见的图搜索算法,它通过队列来实现。BFS从起始节点开始,依次将其相邻的节点加入队列,并逐层向外扩展搜索,直到找到目标节点或队列为空。BFS通常用于求解最短路径等问题。
from collections import defaultdict
class Graph:
def __init__(self):
self.graph = defaultdict(list)
def add_edge(self, u, v):
self.graph[u].append(v)
def bfs(self, start, target):
visited = [False] * (max(self.graph) + 1)
queue = []
path = []
queue.append(start)
visited[start] = True
while queue:
s = queue.pop(0)
path.append(s)
if s == target:
print("BFS Path:", path)
break
for i in self.graph[s]:
if not visited[i]:
queue.append(i)
visited[i] = True
# 创建图实例
g = Graph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.add_edge(3, 3)
start_node = 2
target_node = 3
print("Starting from node", start_node)
print("Searching for node", target_node)
# 使用BFS算法搜索路径
g.bfs(start_node, target_node)
通过以上示例代码,我们展示了如何使用DFS和BFS算法在图中搜索从起始节点到目标节点的路径。这两种算法在不同情况下有着不同的应用,可以根据具体问题的需求选择合适的算法。