目录

力扣526. 优美的排列

解析代码

---

力扣526. 优美的排列

526. 优美的排列

难度 中等

假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件 之一 ，该数组就是一个 优美的排列 ：

• perm[i] 能够被 i 整除
• i 能够被 perm[i] 整除

给你一个整数 n ，返回可以构造的 优美排列 的 数量 。

示例 1：

输入：n = 2
输出：2
解释：
第 1 个优美的排列是 [1,2]：
    - perm[1] = 1 能被 i = 1 整除
    - perm[2] = 2 能被 i = 2 整除
第 2 个优美的排列是 [2,1]:
    - perm[1] = 2 能被 i = 1 整除
    - i = 2 能被 perm[2] = 1 整除

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 15

class Solution {
public:
    int countArrangement(int n) {

    }
};

---

解析代码

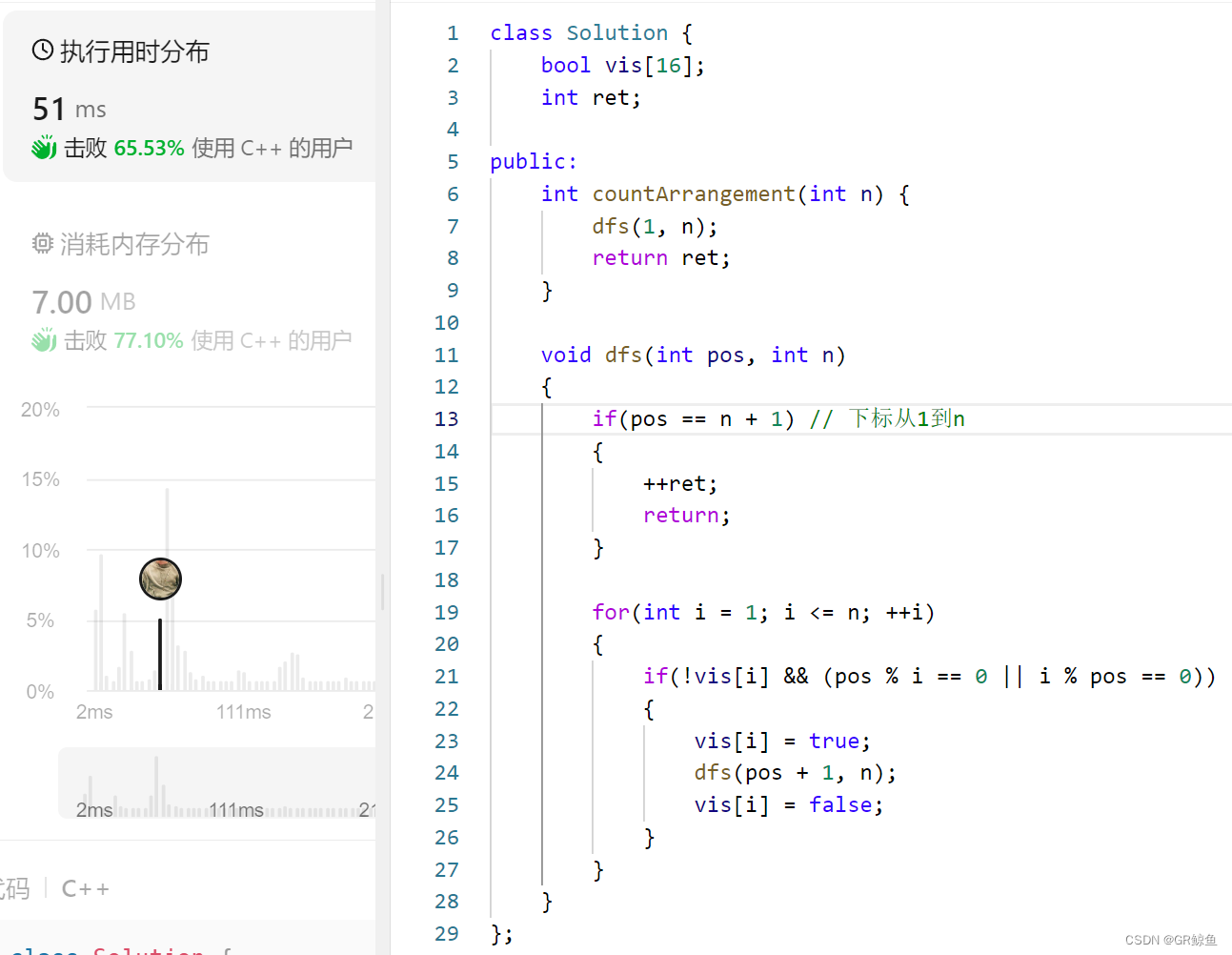
       题意是在每一个位置上考虑所有的可能情况并且不能出现重复。所以可以通过深度优先搜索的方式，不断地枚举每个数在当前位置的可能性，并回溯到上一个状态，直到枚举完所有可能性，得到正确的结果。

        需要定义一个变量用来记录所有可能的排列数量，一个一维数组 visited 标记元素，然后从第一个位置开始进行递归。递归函数作用：在当前位置填入一个合理的数字，查找所有满足条件的排列。

class Solution {
    bool vis[16];
    int ret;

public:
    int countArrangement(int n) {
        dfs(1, n);
        return ret;
    }

    void dfs(int pos, int n)
    {
        if(pos == n + 1) // 下标从1到n
        {
            ++ret;
            return;
        }
        
        for(int i = 1; i <= n; ++i)
        {
            if(!vis[i] && (pos % i == 0 || i % pos == 0))
            {
                vis[i] = true;
                dfs(pos + 1, n);
                vis[i] = false;
            }
        }
    }
};