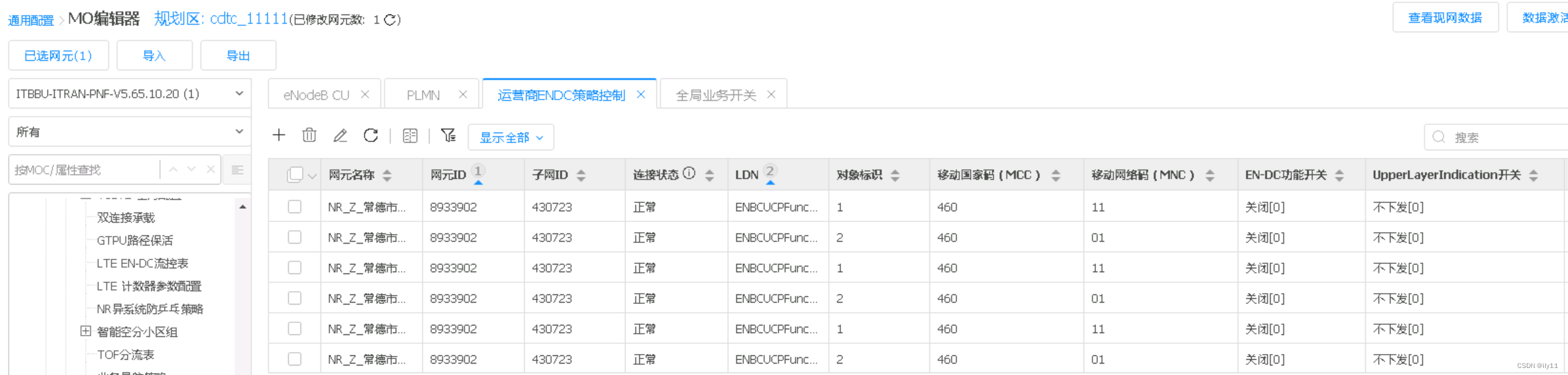
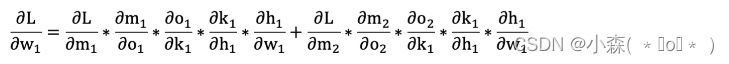本文作为对图神经网络的补充。主要内容是看书。
仅包含Introduction to Graph Theory前五章以及其他相关书籍的相关内容(如果后续在实践中发现前五章不够,会补上剩余内容)
引入
什么是图?
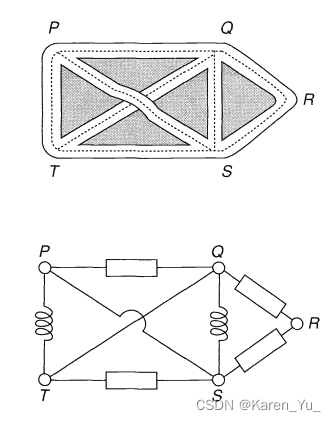
如上图所示的路线图和电路图都可以使用点和线表示,如下图:

图中的点P,Q,R,S和T被称为顶点(vertices),而图中的线被称为边(edges)。整张图被称为图(graph)。注意PS和QT两条线相交点并不是顶点,参考前面的图,这里的“焦点”并不是路口或者是两条电线教会的地方。
顶点的度(degree),是以该顶点为终点的边的个数,比如图中的顶点Q的度是4(PQ,TQ,SQ,RQ)。
上面这张图也可以表示其他的情况,比如,P,Q,R,S和T表示足球队,边代表队伍之间的比赛,那么队伍P就和Q,S和T三个队伍比赛过,但是没有与队伍R比过赛。这种情况下,度就可以理解为对应队伍参加比赛的数目。
如果我们把PS边扯到矩形PQST外面,得到的图(⬇️)荏苒可以告诉我们P S两个地点之间有一条路/P S之间连了一条电线/P S两个足球队之间进行了比赛。我们丢失的信息可能是路线的长度或者电线是直的。

因此,图仅仅代表点之间是如何连接的,任何测量得到的属性都不重要。因此虽然PS被扯到外面了,但是与前面的图是同一个图。

类似的,即使⬆️这张图长得完全不像了,但是仍然是同一张图。
现在,我们假设QS、ST道路拥堵,我们需要建造更多的路来缓解交通压力,如下图:

此时,QS、ST之间的边被称为多重边(multiple edges)。
现在,我们有一辆车要在P点停车(感觉这里说做U turn更好理解),此时在P点加一条边,此时这条边被称为自环(loop)

没有loop以及multiple edges的图被称为简单图(simple graphs)

将道路设置为单行道,即为有向图(directed graphs,简写为digraphs),如上图所示。单行道的方向使用箭头表示。
许多图论都包含了各种各样的“移动方式”,即从一个顶点移动到另一个顶点。比如从P点到Q点,我们可以P —> Q —> R,P —> S —> Q —> T —> S —> R,前者走了两步,后者走了五步。如果同一个顶点出现次数不超过一次,则称这种“移动方式”为一条路(path)。
P —> T —> S —> R为一条路
Q —> S —> T —> Q是一个环
这里关于Eulerian和Hamiltonian graph的描述不是很清楚,采用其他材料补充。
在访问每个顶点时沿着每条边正好走一次的回路被称为欧拉回路(Eulerian circuit),这个图被称为欧拉图(Eulerian graph)(死去的记忆开始攻击我了)
如果连通图中存在闭合遍历,则该图称为哈密顿图(Hamiltonian Graph),除了根顶点或起始顶点外,该图的每个顶点都经过一次。哈密顿图的另一个定义是如果有一个连通图,它包含哈密顿电路,那么这个图就被称为哈密顿图。
Certain graph problems deal with finding a path between two vertices such that each edge is traversed exactly once, or finding a path between two vertices while visiting each vertex exactly once. These paths are better known as Euler path and Hamiltonian path respectively.
Mathematics | Euler and Hamiltonian Paths - GeeksforGeeks
有些图有两个或者更多的部分组成->非连通图
任意两个顶点之间都连了一条路径->连通图

如果每一对顶点之间只连了一条边->称为树(tree)
可以看出树是连通图,但是没有环

图的边没有交叉的图称为平面图(planar graph)


(在第6章中介绍的是染色问题,提到了高中的时候用到过的四色定理,考虑有空去看看~)
定义
图

如上图,简单图G的顶点集合为V(G),{u, v, w, z},边的集合为E(G),包含:uv, uw, vw, wz
在任何简单图中,最多有一条边连接给定的一对顶点。
简单图的很多结论可以推广到更general的图中(即使加上环和多重边)



图:
其中V表示顶点的集合,E是未排序的顶点对的集合,E中的元素即为边。
相邻(adjacent):假设u v是图的两个顶点,若有
,则称u v是相邻的,即
是图G中的一条边,称u为v的邻居(neighbour)。
关联(incident):若顶点v和边e的关系为,则称顶点v和边e关联。
自环(loop):
这里的(v,v)表示边连接的两个顶点是同一个
多重边(multiple edge):当一条边在边的集合E中出现多次,称为多重边
简单图:没有环&多重边
同构(Isomorphism)


若
之间的顶点有一一对应关系,且
中连接任意两个顶点的边的个数与
中对应相等,则称
同构。
推论:G_1与G_2同构,则G_2与G_1同构(可逆)
G_1与G_2同构,G_2与G_3同构,则G_1与G_3同构(传递)
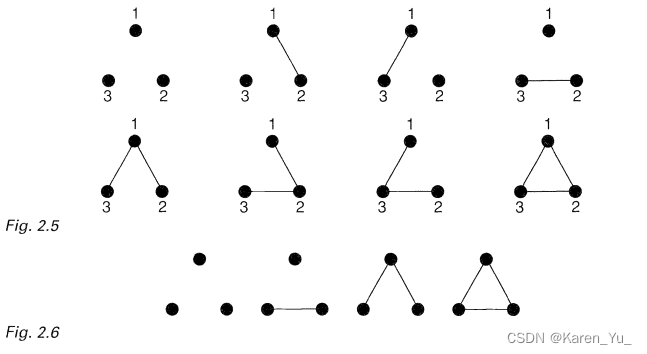
labelled graph和unlabelled graph(直接看图,上面的是labelled,下面是unlabelled)
连通(connectedness)

我们可以把两个图合并在一起,得到一个更大的图,假设现在有两个图以及图
并且两个图的顶点的集合(
、
)是不相连的,则图的union
即为顶点集合和边集合的union
、
之前讨论的大部分图都是连通的(不能被表述为两个图的union),如果可以拆成两个图,那么就是非连通图

任何非连通图G都可以表示成连通图的union,这里的连通图被称为连通块/连通分量(connected component)
相邻
当图G的顶点v和w之间有一条边vw,我们称顶点v和w是相邻(adjacent)的,且与边相关(incident)。类似的,如果两条边e和f有一个公共的顶点,则称这两条边相邻。

邻接矩阵&关联矩阵
adjacency and incidence matrices


假设有n个顶点,邻接矩阵定义为一个nxn的矩阵,若顶点i和顶点j之间有一条边,则位置(i,j)为1,否则为0。任何邻接矩阵为实矩阵且为对称阵
假设有n个顶点,m条边,关联矩阵为一个nxm的矩阵,若顶点与边相关(这条边有一段连着这个顶点)则为1,否则为0。
度
如果顶点v的度为0,则称该顶点为孤立点(isolated)


如上图所示的图的度序列为(1,3,6,8)(可以看到环会带来两个度)
handshaking lemma:任何图的所有顶点的度的和是偶数。
 说明如果几个人握手,总的握手数目一定是偶数
说明如果几个人握手,总的握手数目一定是偶数
子图
图G的子图是一个顶点都在V(G)内,边都在E(G)内的图。

导出子图(induced subgraph):是子图,但是摘出来所有完整的边(如果某个点有多条边,只选取边的另一边连着的顶点也在选取的顶点集合中的边。
生成子图(spanning subgraph):是子图,但是顶点全都选出来了
特殊的图

null graphs:边的集合为空的图。注意null graph的每个顶点都是isolated的。
complete graphs:每一对不同的顶点是邻接的简单图。如果有n个顶点,那么边的数目为n(n-1)/2(见下图)

regular graphs:图的每个顶点都有相同的度(见下图)。如果图的每个顶点的度为r,则称图为regular of degree r或r-regular(r阶正则图)。
下图同样称为Petersen graph,是cubic graphs的一个例子,cubic graphs指的是3阶正则图

cycle graphs:二阶正则图。
path graphs:cycle graphs去掉一条边
wheel:给cycle graphs中的每个点都另外一起连到一个新的顶点
如下图:

platonic graphs:属于正则图

bipartite graphs(二部图/二分图):如果图G的顶点集合可以被分为两个不相交的集合A和B,使得图G的每条边都分别连接A中的顶点和B中的顶点。
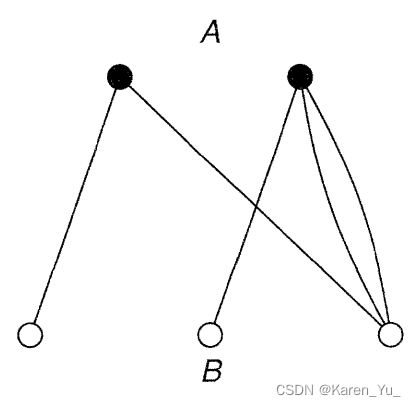
cubes:正则二部图
路径和循环
连通性
给定一个图G。G中的一条线路(walk)是一个有限的边的序列,可以表示成:
或者
任意两条连续的边是邻接的或者是相同的(有一个自环)。我们称v_0为线路的初始顶点(initial vertex),v_m为线路的最终顶点(final vertex),并且称这个过程为从v_0到v_m的线路(a walk from v_0 to v_m)。线路中经过的边的条数称为线路的长度(length)

但是线路的概念往往太过于笼统了->引入轨迹(trail)的概念。轨迹指的是所有的边都是distinct的线路,如果同时能保证顶点也是distinct,就称为途径(path)。
如果轨迹或途径是封闭(closed)的(即初始顶点=最终顶点,v_0 = v_m)。至少包含一条边的封闭的途径称为环(cycle),请注意,任何的自环以及多重边都是环。

若G为二部图,则G的每个环的长度都是偶数

连通图:任何一对顶点时图中一条途径的两端
非连通图:⬆️不满足
Eulerian graphs
如果一个连通图G存在一条封闭的轨迹包含G中所有的边,则称这条轨迹为Eulerian trail。注意要求每条边都要遍历且只能走一次(一笔画)

如果一个非欧拉图存在一条轨迹可以包含所有的边,称为semi-Eulerian。上图由左到右依次为欧拉图,半欧拉图,非欧拉图。
七桥问题:

引理:若G的每个顶点的度都至少为2,那么G包含一个环
定理:当且仅当连通图G的每个顶点的度都是偶数,这个图才是Eulerian
(题外话,这不就是一笔画问题咩)
Hamiltonian graphs
哈密顿图
是否包含一条封闭的轨迹通过且只通过一次图G中的所有顶点。

一些算法
详见https://www.maths.ed.ac.uk/~v1ranick/papers/wilsongraph.pdf47页
树
本章暂时跳过
平面性
平面图
平面图(planar graph)指的是图可以被画在一个平面上并且避免交叉(即:没有任何两条边在除了顶点意外的地方在几何上相交)

把左图的一条边扯到外边(中间的图)就得到了一个平面图


同胚的 (homeomorphic):若两个图都可以通过向同一个图的边加入新的度为2的顶点,称两个图同胚


对偶图

图论(十三)——平面图和对偶图-CSDN博客
在G的每个面中选择点v*作为G*的顶点,对应G的边e画边e*穿过e,但是不穿过G的其他边,并将与e相邻的面的顶点v*连接起来,这些线就是G*的边
参考:
https://www2.math.ethz.ch/education/bachelor/lectures/fs2016/math/graph_theory/graph_theory_notes.pdf
https://sitn.hms.harvard.edu/flash/2021/graph-theory-101/
https://cseweb.ucsd.edu/~dakane/Math154/154-textbook.pdf
https://www.maths.ed.ac.uk/~v1ranick/papers/wilsongraph.pdf




![[Java、Android面试]_24_Compose为什么绘制要比XML快?(高频问答)](https://img-blog.csdnimg.cn/direct/c07f237dd1bc465fa8a91aa14bf585ac.png)