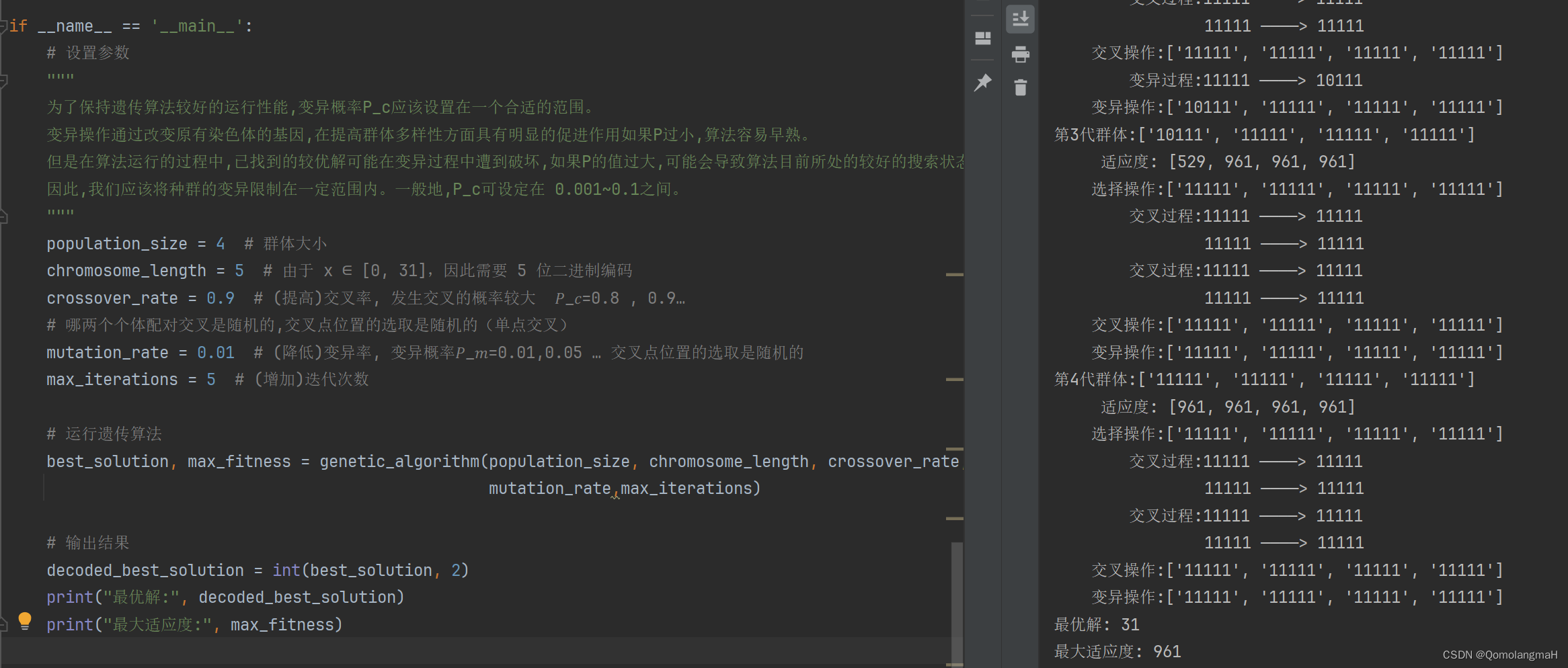
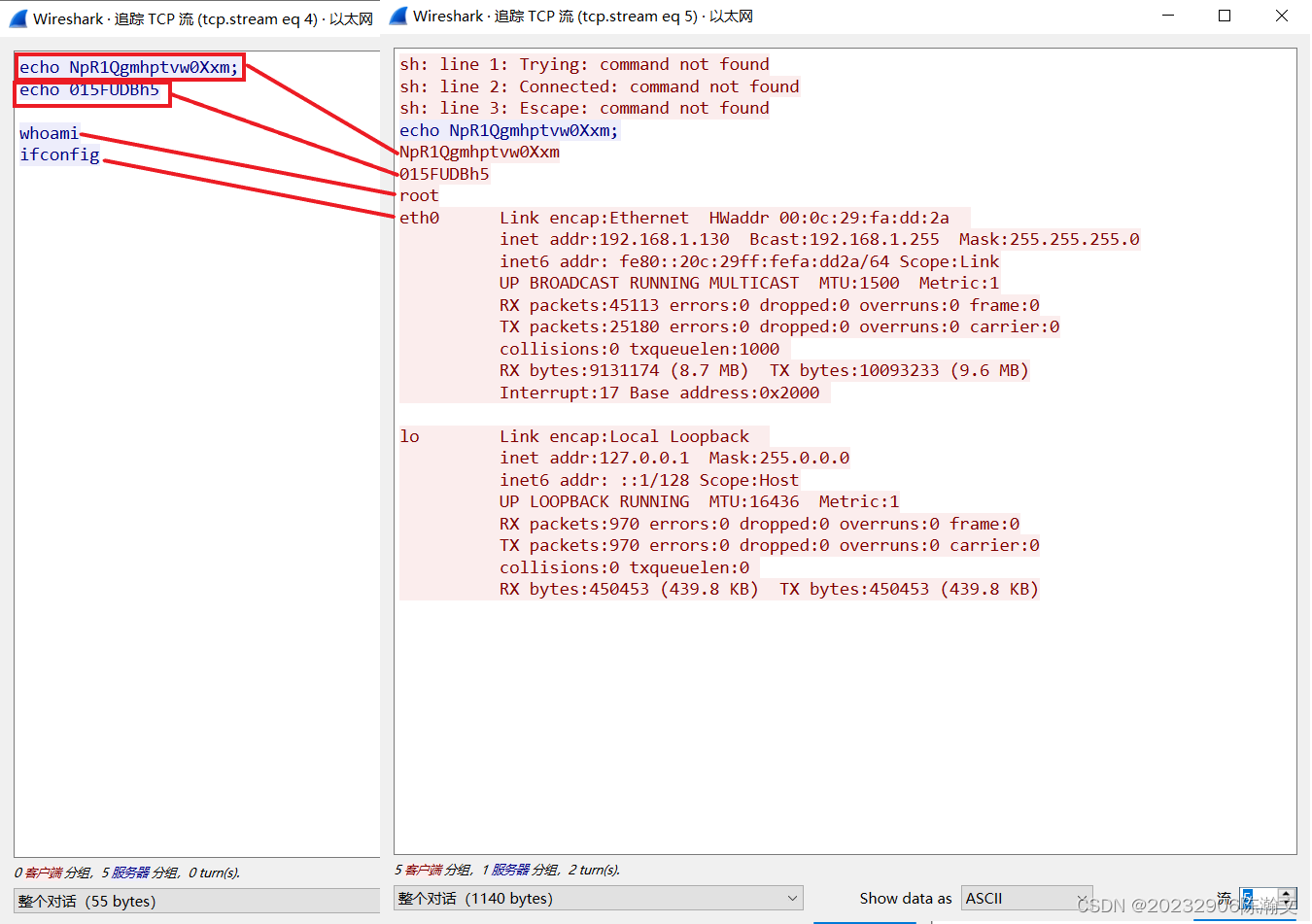
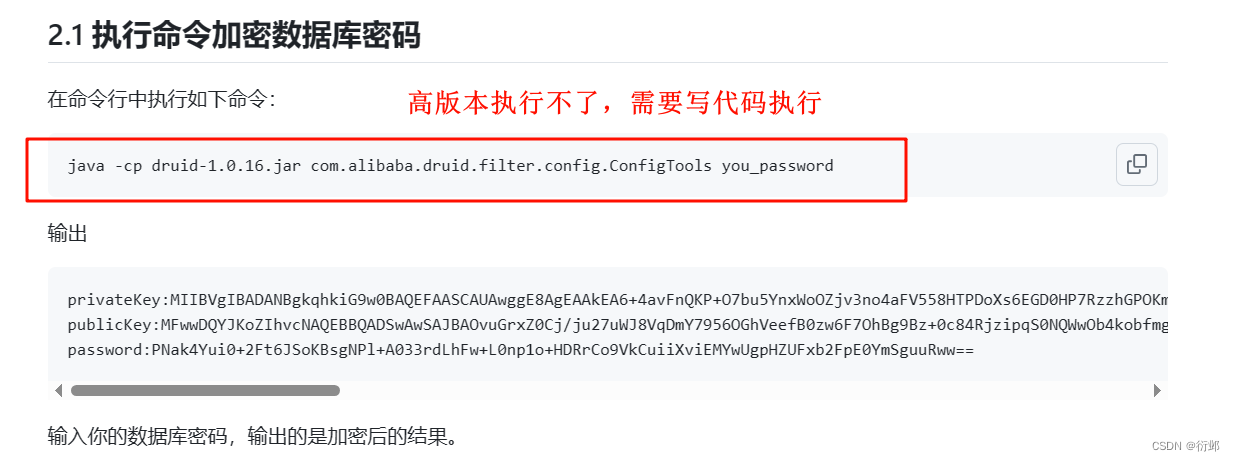
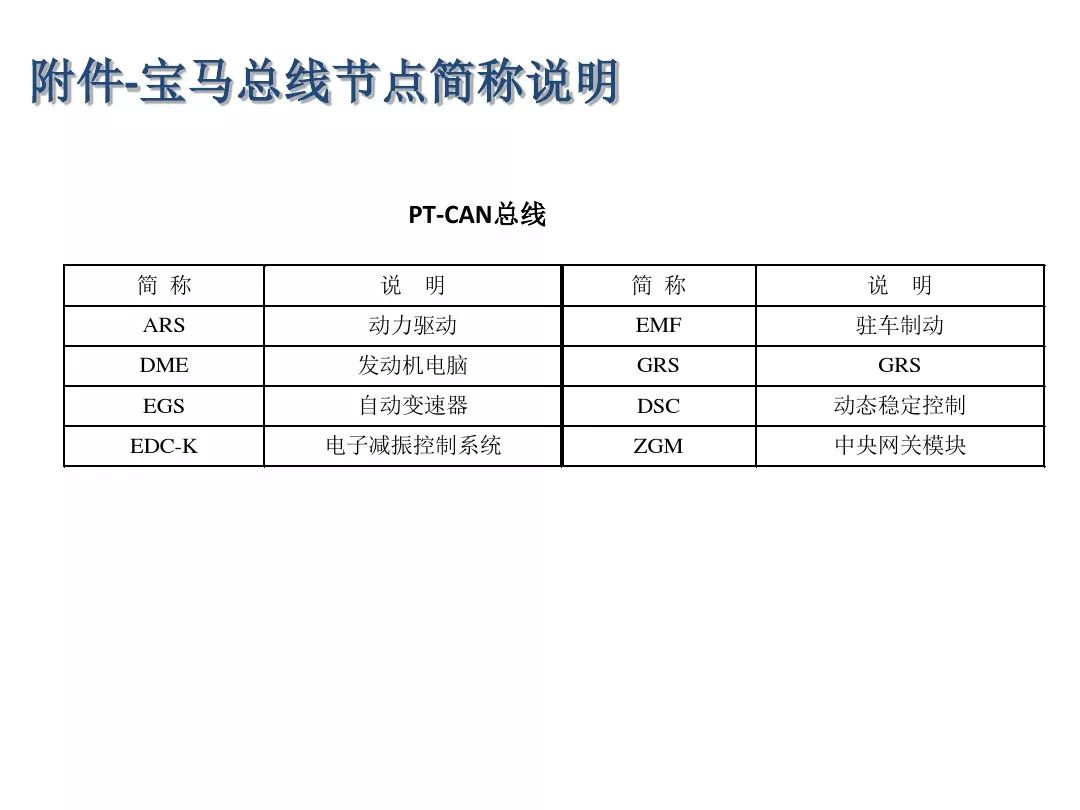
水了个圈钱杯省一，不过估计国赛也拿不了奖，但还是小小挣扎一下。

什么是二分图：G=(V,E)是一个无向图，若顶点V可以分为两个互不相交的子集A,B，并图中的每一条边（i,j)所关联的ij属于不同的顶点集，那么G就是一个二分图。

如何判定？当前仅当图中不含有奇数环。

如果图中有奇数环，假如是一个三角形123，那么1，2一定在不同的集合，2，3一定在不同的集合，那么13就在同一个集合，矛盾。

对于充分性，黑白交替染色即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node{
    int u,next;
};
int head[100010],col[100010],cnt;
node edge[200020];
void merge(int u1,int v)
{
    edge[++cnt].u=v;
    edge[cnt].next=head[u1];
    head[u1]=cnt;
}
bool dfs(int ck,int colo)
{
    col[ck]=colo;
    for(int i=head[ck];i!=-1;i=edge[i].next)
    {
        int coco=edge[i].u;
        if(col[coco])
        {
            if(col[coco]==colo) return 0;
        }
        else{
            if(dfs(coco,3-colo)==0) return 0;
        }
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int uu,vv;
        scanf("%d%d",&uu,&vv);
        merge(uu,vv);
        merge(vv,uu);
    }
    bool flag=1;
    for(int i=1;i<=n;i++)
    {
        if(!col[i])
        {
            if(dfs(i,1)==0){
                flag=0;
                break;
            }
        }
    }
    if(flag==1) cout<<"Yes";
    else cout<<"No";
}

二分图的最大匹配：匈牙利算法

枚举一下左边的点，去右边找匹配，如果已经有了，那么看看被占的那个点有没有其他选择，于是就是一个递归，唯一不同就是那个点不能去访问，我们用st存是否访问过即可，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n1,n2,m;
struct node{
    int dian,next;
}edge[100010];
int head[600],cnt;
bool st[2000];
int match[2000];
void merge(int x,int y)
{
    edge[++cnt].dian=y;
    edge[cnt].next=head[x];
    head[x]=cnt;
}
bool find(int x)
{
    for(int i=head[x];i!=-1;i=edge[i].next)
    {
        int ck=edge[i].dian;
        if(!st[ck])
        {
            st[ck]=1;
            if(match[ck]==0||find(match[ck]))
            {
                match[ck]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    cin>>n1>>n2>>m;
    memset(head,-1,sizeof(head));
    while(m--)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        merge(u,v);
    }
    int res=0;
    for(int i=1;i<=n1;i++)
    {
        memset(st,0,sizeof(st));
        if(find(i)) res++;
    }
    cout<<res;
}