【计算智能】基本遗传算法在优化问题中的应用与实验【理论到程序】

文章目录

1. 引言：遗传算法简介
2. 基本遗传算法（SGA）
- 2.1 基本遗传算法的构成要素
- - 1. 染色体编码
  - 2. 适应度函数
  - 3. 遗传算子
- 2.2 实验设计与方法
- - 1. 算法流程
  - 2. 伪代码
  - 3. python实现
  - - 1. 导入模块
    - 2. 目标函数 f(x)
    - 3 初始化种群
    - 4. 计算适应度
    - 5. 选择操作：轮盘赌选择
    - 6. 单点交叉操作
    - 7. 变异操作
    - 8. 遗传算法
    - 9. 主程序
- 2.3 实验结果与分析
- 2.4 结论与展望
3. 遗传算法的改进
4. 遗传算法的应用
5. 代码整合
- 6. 随笔

摘要： 本文将介绍遗传算法在解决优化问题中的应用，并通过实验展示了遗传算法的基本原理和实现过程。选取一个简单的二次函数作为优化目标，利用遗传算法寻找其在指定范围内的最大值。

1. 引言：遗传算法简介

遗传算法是一种启发式优化算法，模拟了生物进化的过程，通过选择、交叉和变异等操作来搜索解空间中的最优解或近似解，其在解决复杂的优化问题和搜索空间较大的问题时表现出色。

2. 基本遗传算法（SGA）

基本遗传算法(Simple Genetic Algorithm : SGA)又称为简单遗传算法，只使用选择算子、交叉算子和变异算子这三种基本的遗传算子。其遗传操作简单、容易理解，是其它遗传算法的雏形和基础。

2.1 基本遗传算法的构成要素

基本遗传算法由染色体编码方法、适应度函数和遗传算子三个主要要素组成。下面将对每个要素进行详细说明：

1. 染色体编码

染色体编码方法指将问题的解空间映射到染色体上的过程。通常采用二进制编码方法，将问题的解表示为一个二进制串。例如，在解决一个优化问题时，可以将每个解编码为一个二进制串，其中每一位代表一个决策变量的取值。除了二进制编码，还可以使用整数编码、浮点数编码或字符编码，根据问题的特性选择合适的编码方法。

2. 适应度函数

适应度函数（又称适应值/适应函数）用于评价染色体的优劣程度，即衡量染色体对问题解的贡献或适应程度。适应度函数的设计应与问题的特性密切相关，通常通过问题的目标函数来定义。例如，在优化问题中，适应度函数可以直接使用目标函数的值作为染色体的适应度，或根据问题的约束条件进行适当的调整。

3. 遗传算子

遗传算子是基本遗传算法的核心组成部分，包括选择算子、交叉算子和变异算子。

选择算子（Selection）：又称复制算子，按照某种策略从父代中挑选个体进入下一代，常见的选择算子包括比例选择、轮盘赌选择、锦标赛选择等。
- 选择算子的目标是按染色体的适应度进行选择，以保留适应度较高的个体，促进种群的进化。
交叉算子（Crossover）：又称杂交算子，用于从选定的父代染色体中产生子代染色体。常见的交叉算子包括单点交叉、多点交叉等。
- 交叉算子通过交换染色体的部分信息产生新的个体，增加种群的多样性。
变异算子（Mutation）：用于对染色体的个别基因进行随机变化。
- 变异算子的作用是引入种群的随机性，避免陷入局部最优解。常见的变异算子包括单点变异、均匀变异等，通常具有较小的概率，以保持种群的稳定性。

基本遗传算法能够模拟自然进化的过程，通过选择、交叉和变异等遗传操作逐步优化种群，求得问题的最优解或近似解。

2.2 实验设计与方法

1. 算法流程

2. 伪代码

Procedure GeneticAlgorithm()
    t = 0 // 初始化迭代次数
    InitializePopulation(P(t)) // 初始化种群
    Evaluate(P(t)) // 评估种群中个体的适应度
    Best = KeepBest(P(t)) // 保留当前最优个体

    while (not TerminationConditionMet()) do
        P(t) = Selection(P(t)) // 选择操作
        P(t) = Crossover(P(t)) // 交叉操作
        P(t) = Mutation(P(t))  // 变异操作
        t = t + 1 // 更新迭代次数
        P(t) = P(t-1)
        Evaluate(P(t)) // 重新评估种群中个体的适应度
        if (BestIndividual(P(t)) > Best) then
            Best = ReplaceBest(P(t)) // 更新最优个体
        end if
    end while

    return Best // 返回找到的最优解
End Procedure

3. python实现

本实验选择了一个简单的二次函数 $x^2, x \in [0, 31]$ 作为优化目标：

对函数的解空间进行二进制编码
随机生成初始种群
计算每个个体的适应度使用选择、交叉和变异操作优化种群，直到达到设定的迭代次数。
评估最优解的适应度并输出结果。

1. 导入模块

import random

2. 目标函数 f(x)

def f(x):
    return x ** 2

3 初始化种群

def initialize_population(population_size, chromosome_length):
    return [bin(random.randint(0, 31))[2:].zfill(chromosome_length) for _ in range(population_size)]

生成指定大小的种群，每个个体都是一个长度为 chromosome_length （本实验为5）的二进制字符串，代表一个取值范围在 0 到 31 之间的整数。函数可以拆分为：

def initialize_population(size):
    return [encode(random.randint(0, 31)) for _ in range(size)]

染色体编码函数 encode(x)

def encode(x):
    return bin(x)[2:].zfill(5)

将整数 x 编码成一个长度为 5 的二进制字符串。内置的 bin() 函数将整数转换为二进制字符串，然后使用 zfill() 函数填充到长度为 5。

4. 计算适应度

def fitness(chromosome):
    return f(decode(chromosome))

这个函数计算染色体的适应度，即目标函数的取值。它通过先解码染色体，然后将解码后的值代入目标函数 f(x) 中来计算适应度。

5. 选择操作：轮盘赌选择

def selection(population, fitness_values):
    total_fitness = sum(fitness_values)
    # 计算每个个体被选中的概率
    probabilities = [fitness / total_fitness for fitness in fitness_values]
    # print("\t选择概率: {}".format(probabilities))
    selected_population = []
    for _ in range(len(population)):
        selected_individual = random.choices(population, weights=probabilities)[0]
        # print("\t被选个体: {}".format(selected_individual))
        selected_population.append(selected_individual)
    return selected_population

从轮盘赌选择的机制中可以看到,较优染色体的P值较大,被选择的概率就相对较大。但由于选择过程具有随机性,并不能保证每次选择均选中这些较优的染色体,因此也给予了较差染色体一定的生存空间。

6. 单点交叉操作

def crossover(parent1, parent2):
    crossover_point = random.randint(1, len(parent1) - 1)
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    print("\t\t交叉过程:{} ————> {}\n\t\t\t\t{} ————> {}".format(parent1, child1, parent2, child2))
    return child1, child2

随机选择一个交叉点，然后将两个父代个体在交叉点处进行交换，生成两个新的子代个体。

7. 变异操作

def mutation(population, mutation_rate):
    mutated_population = []
    for individual in population:
        mutated_individual = ''
        for bit in individual:
            if random.random() < mutation_rate:
                mutated_bit = '0' if bit == '1' else '1'
            else:
                mutated_bit = bit
            mutated_individual += mutated_bit
        if mutated_individual != individual:
            print("\t\t变异过程:{} ————> {}".format(individual, mutated_individual))
        mutated_population.append(mutated_individual)
    return mutated_population

对于染色体中的每个基因，根据指定的变异率，以一定概率对其进行变异（由 0 变为 1 或由 1 变为 0）。

8. 遗传算法

def genetic_algorithm(population_size, chromosome_length, crossover_rate, mutation_rate, max_iterations):
    population = initialize_population(population_size, chromosome_length)
    best_individual = None
    best_fitness = float('-inf')
    print(f"初始化群体:{population}")
    for iteration in range(max_iterations):
        print(f"第{iteration}代群体:{population}")
        # 评估种群中所有个体的适应度
        fitness_values = evaluate_population(population)
        print(f"\t 适应度: {fitness_values}")
        # 选择操作
        population = selection(population, fitness_values)
        print(f"\t选择操作:{population}")
        # 交叉操作
        for i in range(0, len(population), 2):
            if random.random() < crossover_rate:
                population[i], population[i + 1] = crossover(population[i], population[i + 1])
        print(f"\t交叉操作:{population}")

        # 变异操作
        population = mutation(population, mutation_rate)
        print(f"\t变异操作:{population}")

        # 更新最优个体
        max_fitness = max(fitness_values)
        if max_fitness > best_fitness:
            best_fitness = max_fitness
            best_individual = population[fitness_values.index(max_fitness)]

    return best_individual, best_fitness

9. 主程序

if __name__ == '__main__':
    # 设置参数
    population_size = 4  # 群体大小
    chromosome_length = 5  # 由于 x ∈ [0, 31]，因此需要 5 位二进制编码
    crossover_rate = 0.9  # (提高)交叉率, 发生交叉的概率较大  𝑃_𝑐=0.8 , 0.9…
    # 哪两个个体配对交叉是随机的,交叉点位置的选取是随机的（单点交叉）
    mutation_rate = 0.01  # (降低)变异率, 变异概率𝑃_𝑚=0.01,0.05 … 交叉点位置的选取是随机的
    max_iterations = 2  # (增加)迭代次数

    # 运行遗传算法
    best_solution, max_fitness = genetic_algorithm(population_size, chromosome_length, crossover_rate, mutation_rate,
                                                   max_iterations)

    # 输出结果
    decoded_best_solution = int(best_solution, 2)
    print("最优解:", decoded_best_solution)
    print("最大适应度:", max_fitness)

在这里插入图片描述

2.3 实验结果与分析

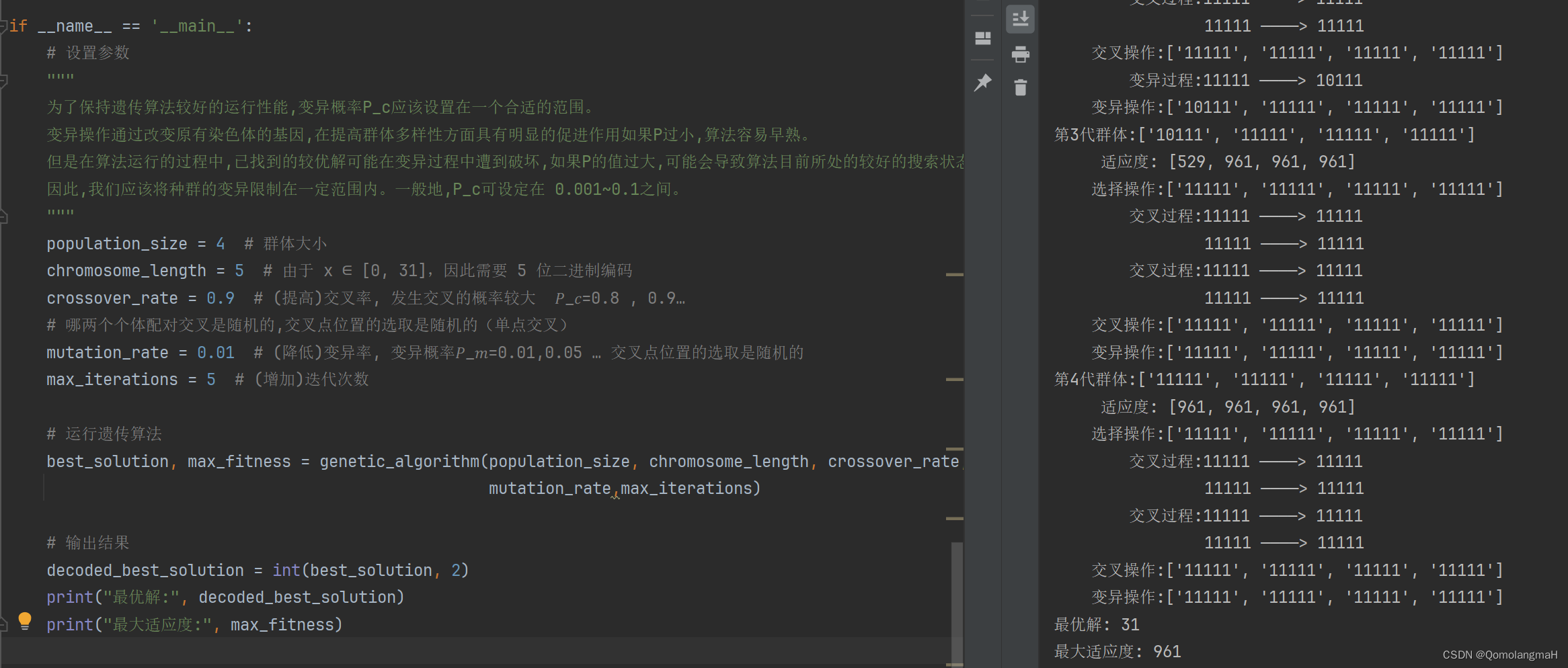
为了保持遗传算法较好的运行性能,变异概率P_c应该设置在一个合适的范围。变异操作通过改变原有染色体的基因,在提高群体多样性方面具有明显的促进作用如果P过小,算法容易早熟。但是在算法运行的过程中,已找到的较优解可能在变异过程中遭到破坏,如果P的值过大,可能会导致算法目前所处的较好的搜索状态倒退回原来较差的情况。因此,我们应该将种群的变异限制在一定范围内。一般地,P_c可设定在 0.001~0.1之间。

实验结果显示，在给定的迭代次数内，遗传算法成功找到了函数 $f(x) = x^2$ 在 $\in [0, 31]$ 范围内的最大值。最终的最优解为 $x = 31$ ，对应的最大适应度为 $f (31) = 961$ 。通过动画展示了遗传算法的演化过程，直观地呈现了优化过程中种群的变化和适应度的提升。

2.4 结论与展望

本文介绍了遗传算法的基本原理和实现过程，并通过实验展示了其在优化问题中的应用。实验结果表明，遗传算法能够有效地搜索解空间，并找到近似最优解。未来，可以进一步研究和优化遗传算法的参数设置、种群初始化和选择策略，以提高算法的性能和收敛速度。

3. 遗传算法的改进

4. 遗传算法的应用

5. 代码整合

import random


# 定义目标函数
def f(x):
    return x ** 2


# 初始化种群
def initialize_population(population_size, chromosome_length):
    return [bin(random.randint(0, 31))[2:].zfill(chromosome_length) for _ in range(population_size)]


# 计算个体的适应度
def evaluate_individual(individual):
    x = int(individual, 2)
    return f(x)


# 评估种群中所有个体的适应度
def evaluate_population(population):
    return [evaluate_individual(individual) for individual in population]


# 选择操作 - 轮盘赌选择算法
"""
从轮盘赌选择的机制中可以看到,较优染色体的P值较大,被选择的概率就相对较大。
但由于选择过程具有随机性,并不能保证每次选择均选中这些较优的染色体,因此也给予了较差染色体一定的生存空间。
"""


def selection(population, fitness_values):
    total_fitness = sum(fitness_values)
    # 计算每个个体被选中的概率
    probabilities = [fitness / total_fitness for fitness in fitness_values]
    # print("\t选择概率: {}".format(probabilities))
    selected_population = []
    for _ in range(len(population)):
        selected_individual = random.choices(population, weights=probabilities)[0]
        # print("\t被选个体: {}".format(selected_individual))
        selected_population.append(selected_individual)
    return selected_population


# 单点交叉操作
def crossover(parent1, parent2):
    crossover_point = random.randint(1, len(parent1) - 1)
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    print("\t\t交叉过程:{} ————> {}\n\t\t\t\t{} ————> {}".format(parent1, child1, parent2, child2))
    return child1, child2


def mutation(population, mutation_rate):
    mutated_population = []
    for individual in population:
        mutated_individual = ''
        for bit in individual:
            if random.random() < mutation_rate:
                mutated_bit = '0' if bit == '1' else '1'
            else:
                mutated_bit = bit
            mutated_individual += mutated_bit
        if mutated_individual != individual:
            print("\t\t变异过程:{} ————> {}".format(individual, mutated_individual))
        mutated_population.append(mutated_individual)
    return mutated_population


# 主程序
def genetic_algorithm(population_size, chromosome_length, crossover_rate, mutation_rate, max_iterations):
    population = initialize_population(population_size, chromosome_length)
    best_individual = None
    best_fitness = float('-inf')
    print(f"初始化群体:{population}")
    for iteration in range(max_iterations):
        print(f"第{iteration}代群体:{population}")
        # 评估种群中所有个体的适应度
        fitness_values = evaluate_population(population)
        print(f"\t 适应度: {fitness_values}")
        # 选择操作
        population = selection(population, fitness_values)
        print(f"\t选择操作:{population}")
        # 交叉操作
        for i in range(0, len(population), 2):
            if random.random() < crossover_rate:
                population[i], population[i + 1] = crossover(population[i], population[i + 1])
        print(f"\t交叉操作:{population}")

        # 变异操作
        population = mutation(population, mutation_rate)
        print(f"\t变异操作:{population}")

        # 更新最优个体
        max_fitness = max(fitness_values)
        if max_fitness > best_fitness:
            best_fitness = max_fitness
            best_individual = population[fitness_values.index(max_fitness)]

    return best_individual, best_fitness


if __name__ == '__main__':
    # 设置参数
    """
    为了保持遗传算法较好的运行性能,变异概率P_c应该设置在一个合适的范围。
    变异操作通过改变原有染色体的基因,在提高群体多样性方面具有明显的促进作用如果P过小,算法容易早熟。
    但是在算法运行的过程中,已找到的较优解可能在变异过程中遭到破坏,如果P的值过大,可能会导致算法目前所处的较好的搜索状态倒退回原来较差的情况。
    因此,我们应该将种群的变异限制在一定范围内。一般地,P_c可设定在 0.001~0.1之间。
    """
    population_size = 4  # 群体大小
    chromosome_length = 5  # 由于 x ∈ [0, 31]，因此需要 5 位二进制编码
    crossover_rate = 0.9  # (提高)交叉率, 发生交叉的概率较大  𝑃_𝑐=0.8 , 0.9…
    # 哪两个个体配对交叉是随机的,交叉点位置的选取是随机的（单点交叉）
    mutation_rate = 0.01  # (降低)变异率, 变异概率𝑃_𝑚=0.01,0.05 … 交叉点位置的选取是随机的
    max_iterations = 2  # (增加)迭代次数

    # 运行遗传算法
    best_solution, max_fitness = genetic_algorithm(population_size, chromosome_length, crossover_rate, mutation_rate,
                                                   max_iterations)

    # 输出结果
    decoded_best_solution = int(best_solution, 2)
    print("最优解:", decoded_best_solution)
    print("最大适应度:", max_fitness)