目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
- 1.11 神经网络的权重初始化(Weight Initialization for Deep Networks)
- 1.12 梯度的数值逼近(Numerical approximation of gradients)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
1.11 神经网络的权重初始化(Weight Initialization for Deep Networks)
上节课,我们学习了深度神经网络如何产生梯度消失和梯度爆炸问题,最终针对该问题,我们想出了一个不完整的解决方案,虽然不能彻底解决问题,却很有用,有助于我们为神经网络更谨慎地选择随机初始化参数,为了更好地理解它,我们先举一个神经单元初始化地例子,然后再演变到整个深度网络。
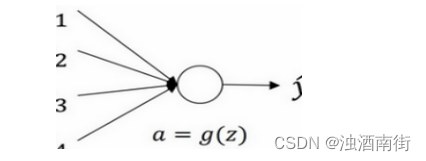
我们来看看只有一个神经元的情况,然后才是深度网络。
单个神经元可能有 4 个输入特征,从 x 1 x_1 x1到 x 4 x_4 x4,经过a= g(z)处理,最终得到 y ^ \hat{y} y^,稍后讲深度网络时,这些输入表示为 a [ l ] a^{[l]} a[l],暂时我们用𝑥表示。
z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n , b = 0 z = w_1x_1 + w_2x_2 + ⋯ + w_nx_n,b = 0 z=w1x1+w2x2+⋯+wnxn,b=0,暂时忽略𝑏,为了预防𝑧值过大或过小,你可以看到𝑛越大,你希望 w i w_i wi越小,因为z是 w i x i w_ix_i wixi的和,如果你把很多此类项相加,希望每项值更小,最合理的方法就是设置 w i = 1 n w_i =\frac{1}{n} wi=n1,𝑛表示神经元的输入特征数量,实际上,你要做的就是设置某层权重矩阵 w [ l ] = n p . r a n d o m . r a n d n ( s h a p e ) ∗ n p . s q r t ( 1 n l − 1 ) w^{[l]} = np. random. randn(shape) ∗ np. sqrt(\frac{1}{n^{l-1}}) w[l]=np.random.randn(shape)∗np.sqrt(nl−11), n l − 1 n^{l-1} nl−1就是我喂给第𝑙层神经单元的数量(即第𝑙 − 1层神经元数量)。

结果,如果你是用的是 Relu 激活函数,而不是
1
n
\frac{1}{n}
n1,方差设置为
2
n
\frac{2}{n}
n2,效果会更好。你常常发现,初始化时,尤其是使用 Relu 激活函数时,
g
[
l
]
(
z
)
=
R
e
l
u
(
z
)
g^{[l]}(z) = Relu(z)
g[l](z)=Relu(z),它取决于你对随机变量的熟悉程度,这是高斯随机变量,然后乘以它的平方根,也就是引用这个方差
2
n
\frac{2}{n}
n2。这里,我用的是
n
[
l
−
1
]
n^{[l−1]}
n[l−1],因为本例中,逻辑回归的特征是不变的。但一般情况下𝑙层上的每个神经元都有
n
[
l
−
1
]
n^{[l−1]}
n[l−1]个输入。如果激活函数的输入特征被零均值和标准方差化,方差是 1,𝑧也会调整到相似范围,这就没解决问题(梯度消失和爆炸问题)。但它确实降低了梯度消失和爆炸问题,因为它给权重矩阵𝑤设置了合理值,你也知道,它不能比 1 大很多,也不能比 1 小很多,所以梯度没有爆炸或消失过快。
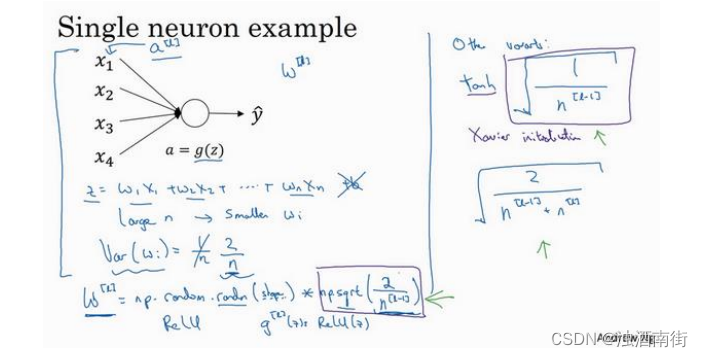
我提到了其它变体函数,刚刚提到的函数是 Relu 激活函数,一篇由 Herd 等人撰写的论文曾介绍过。对于几个其它变体函数,如 tanh 激活函数,有篇论文提到,常量 1 比常量 2的效率更高,对于 tanh 函数来说,它是 1 n l − 1 \sqrt[]{\frac{1}{n^{l-1}}} nl−11,这里平方根的作用与这个公式作用相同(np. sqrt(1𝑛[𝑙−1])),它适用于 tanh 激活函数,被称为 Xavier 初始化。Yoshua Bengio 和他的同事还提出另一种方法,你可能在一些论文中看到过,它们使用的是公式 2 n l − 1 + n l \sqrt[]{\frac{2}{n^{l-1} + n^{l}}} nl−1+nl2。其它理论已对此证明,但如果你想用 Relu 激活函数,也就是最常用的激活函数,我会用这个公式np. sqrt( 2 n l − 1 \frac{2}{n^{l-1}} nl−12),如果使用 tanh 函数,可以用公式 1 n l − 1 \sqrt[]{\frac{1}{n^{l-1}}} nl−11,有些作者也会使用这个函数。
实际上,我认为所有这些公式只是给你一个起点,它们给出初始化权重矩阵的方差的默认值,如果你想添加方差,方差参数则是另一个你需要调整的超级参数,可以给公式np. sqrt( 2 n l − 1 \frac{2}{n^{l-1}} nl−12)添加一个乘数参数,调优作为超级参数激增一份子的乘子参数。有时调优该超级参数效果一般,这并不是我想调优的首要超级参数,但我发现调优过程中产生的问题,虽然调优该参数能起到一定作用,但考虑到相比调优,其它超级参数的重要性,我通常把它的优先级放得比较低。
希望你现在对梯度消失或爆炸问题以及如何为权重初始化合理值已经有了一个直观认识,希望你设置的权重矩阵既不会增长过快,也不会太快下降到 0,从而训练出一个权重或梯度不会增长或消失过快的深度网络。我们在训练深度网络时,这也是一个加快训练速度的技巧。
1.12 梯度的数值逼近(Numerical approximation of gradients)
在实施 backprop 时,有一个测试叫做梯度检验,它的作用是确保 backprop 正确实施。因为有时候,你虽然写下了这些方程式,却不能 100%确定,执行 backprop 的所有细节都是正确的。为了逐渐实现梯度检验,我们首先说说如何计算梯度的数值逼近,下节课,我们将
讨论如何在 backprop 中执行梯度检验,以确保 backprop 正确实施。
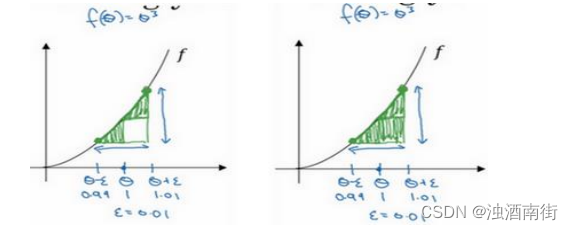
我们先画出函数𝑓,标记为𝑓(𝜃),
f
(
θ
)
=
θ
3
f(θ) = θ^3
f(θ)=θ3,先看一下𝜃的值,假设𝜃 = 1,不增大𝜃的值,而是在𝜃 右侧,设置一个𝜃 + 𝜀,在𝜃左侧,设置𝜃 − 𝜀。因此𝜃 = 1,𝜃 + 𝜀 = 1.01, 𝜃 − 𝜀 =0.99,,跟以前一样,𝜀的值为 0.01,看下这个小三角形,计算高和宽的比值,就是更准确的梯度预估,选择𝑓函数在𝜃 − 𝜀上的这个点,用这个较大三角形的高比上宽,技术上的原因我就不详细解释了,较大三角形的高宽比值更接近于𝜃的导数,把右上角的三角形下移,好像有了两个三角形,右上角有一个,左下角有一个,我们通过这个绿色大三角形同时考虑了这两个小三角形。所以我们得到的不是一个单边公差而是一个双边公差。
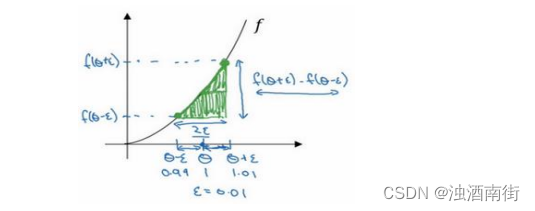
我们写一下数据算式,图中绿色三角形上边的点的值是𝑓(𝜃 + 𝜀),下边的点是𝑓(𝜃 − 𝜀),这个三角形的高度是𝑓(𝜃 + 𝜀) − 𝑓(𝜃 − 𝜀),这两个宽度都是 ε,所以三角形的宽度是2𝜀,高宽比值为
f
(
θ
+
ε
)
−
f
(
θ
−
ε
)
2
ε
\frac{f(θ+ε)−f(θ−ε)}{2ε}
2εf(θ+ε)−f(θ−ε) ,它的期望值接近𝑔(𝜃),
f
(
θ
)
=
θ
3
f(θ) = θ^3
f(θ)=θ3传入参数值:
f
(
θ
+
ε
)
−
f
(
θ
−
ε
)
2
ε
=
(
1.01
)
3
−
(
0.99
)
3
2
∗
0.01
\frac{f(θ+ε)−f(θ−ε)}{2ε} =\frac{(1.01)^3-(0.99)^3}{2*0.01}
2εf(θ+ε)−f(θ−ε)=2∗0.01(1.01)3−(0.99)3
大家可以用计算器算算结果,结果应该是 3.0001,而前面一张幻灯片上面是,当𝜃 = 1时,𝑔(𝜃) = 3 θ 2 θ^2 θ2 = 3,所以这两个𝑔(𝜃)值非常接近,逼近误差为0.0001,前一张幻灯片,我们只考虑了单边公差,即从𝜃到𝜃 + 𝜀之间的误差,𝑔(𝜃)的值为3.0301,逼近误差是 0.03,不是 0.0001,所以使用双边误差的方法更逼近导数,其结果接近于 3,现在我们更加确信,𝑔(𝜃)可能是𝑓导数的正确实现,在梯度检验和反向传播中使用该方法时,最终,它与运行两次单边公差的速度一样,实际上,我认为这种方法还是非常值得使用的,因为它的结果更准确。
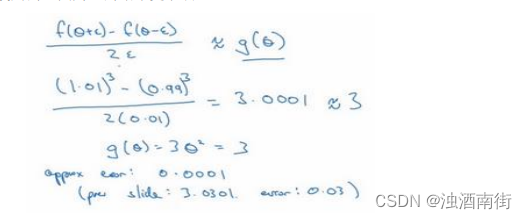
这是一些你可能比较熟悉的微积分的理论,如果你不太明白我讲的这些理论也没关系,导数的官方定义是针对值很小的𝜀,导数的官方
定义是𝑓′(𝜃) =
f
(
θ
+
ε
)
−
f
(
θ
−
ε
)
2
ε
\frac{f(θ+ε)−f(θ−ε)}{2ε}
2εf(θ+ε)−f(θ−ε) ,如果你上过微积分课,应该学过无穷尽的定义,我就不在这里讲了。
对于一个非零的𝜀,它的逼近误差可以写成𝑂( ε 2 ε^2 ε2),ε 值非常小,如果𝜀 = 0.01, ε 2 ε^2 ε2 = 0.0001,大写符号𝑂的含义是指逼近误差其实是一些常量乘以 ε 2 ε^2 ε2,但它的确是很准确的逼近误差,所以大写𝑂的常量有时是 1。然而,如果我们用另外一个公式逼近误差就是𝑂(𝜀),当𝜀小于 1 时,实际上𝜀比 ε 2 ε^2 ε2大很多,所以这个公式近似值远没有左边公式的准确,所以在执行梯度检验时,我们使用双边误差,即 f ( θ + ε ) − f ( θ − ε ) 2 ε \frac{f(θ+ε)−f(θ−ε)}{2ε} 2εf(θ+ε)−f(θ−ε),而不使用单边公差,因为它不够准确。
如果你不理解上面两条结论,所有公式都在这儿,不用担心,如果你对微积分和数值逼近有所了解,这些信息已经足够多了,重点是要记住,双边误差公式的结果更准确,下节课我们做梯度检验时就会用到这个方法。我们讲了如何使用双边误差来判断别人给你的函数𝑔(𝜃),是否正确实现了函数𝑓的偏导,现在我们可以使用这个方法来检验反向传播是否得以正确实施,如果不正确,它可能有 bug 需要你来解决。