TikTok 进展
又是一期定时汇报 TikTok 进展的推文。
上周,美国总统拜登签署了价值 950 亿美元的一揽子对外援助法案。
该法案涉及强制字节跳动剥离旗下应用 TikTok 美国业务,即 针对 TikTok 非卖即禁的"强抢行为"开始进入九个月(270 天)的倒计时。
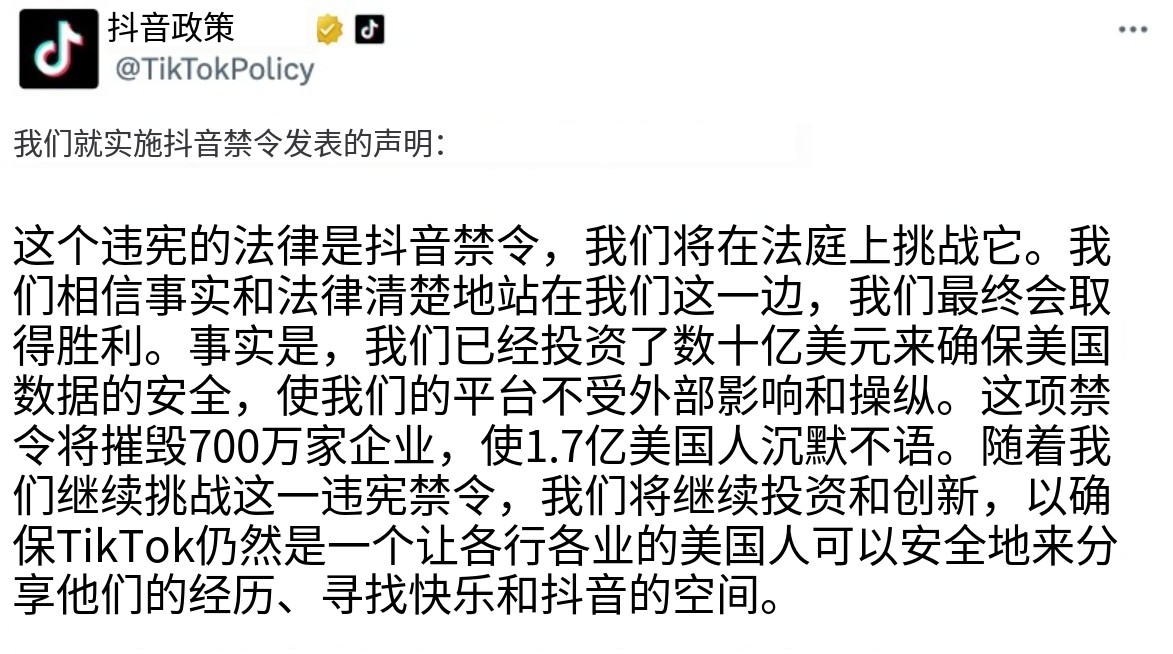
签署法案后,TikTok 官号进行了回应:

之后的几天,陆续出现过一些谣言,其中不乏「传字节跳动已经在密谋出售 TikTok 事宜」这样的消息。
但很快,就被官号高调辟谣了这些「外媒消息」:

TikTok 代言人,也是现任 CEO 周受资也在海外社交媒体中出镜重申:我们哪儿也不去,准备起诉。事实和宪法都站在我们这一边,期待再次获胜。

...
回归主线。
来一道和「字节跳动(社招)」四面相关的算法题。
据投稿人描述,当时其他问题回答得一般,但该算法题顺利做出,最终通过四面,感觉是被这道题救了一命。
题目描述
平台:LeetCode
题号:1879
给你两个整数数组 nums1 和 nums2,它们长度都为 n。
两个数组的 异或值之和 为 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) (下标从 0 开始)。
比方说,[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1 XOR 3) + (2 XOR 2) + (3 XOR 1) = 2 + 0 + 2 = 4。
请你将 nums2 中的元素重新排列,使得异或值之和最小 。
请你返回重新排列之后的 异或值之和 。
示例 1:
输入:nums1 = [1,2], nums2 = [2,3]
输出:2
解释:将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1 XOR 3) + (2 XOR 2) = 2 + 0 = 2 。
示例 2:
输入:nums1 = [1,0,3], nums2 = [5,3,4]
输出:8
解释:将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1 XOR 5) + (0 XOR 4) + (3 XOR 3) = 4 + 4 + 0 = 8 。
提示:
状压 DP
这是一道「状压 DP」模板题。
为了方便,我们令下标从 开始。
「定义
为考虑前
个元素,且对 nums2 的使用情况为
时的最小异或值」。其中
是一个长度为
的二进制数:若
中的第
位为
,说明 nums2[k] 已被使用;若
中的第
位为
,说明 nums2[k] 未被使用。
起始时,只有
,其余均为无穷大 INF。
含义为在不考虑任何数,对 nums2 没有任何占用情况时,最小异或值为
。最终
即为答案。
不失一般性考虑
该如何转移,可以以 nums1[i] 是与哪个 nums2[j] 进行配对作为切入点:
-
由于总共考虑了前 个成员,因此 中 的数量必然为 ,否则 就不是一个合法状态,跳过转移
-
枚举
nums1[i]是与哪一个nums2[j]进行配对的,且枚举的 需满足在 中的第 位值为 ,若满足则有
其中 prev 为将
中的第
位进行置零后的二进制数,即 prev = s ^ (1 << j),符号 ⊕ 代表异或操作。
Java 代码:
class Solution {
public int minimumXORSum(int[] nums1, int[] nums2) {
int n = nums1.length, mask = 1 << n, INF = 0x3f3f3f3f;
int[][] f = new int[n + 10][mask];
for (int i = 0; i <= n; i++) Arrays.fill(f[i], INF);
f[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int s = 0; s < mask; s++) {
if (getCnt(s, n) != i) continue;
for (int j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) == 0) continue;
f[i][s] = Math.min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
}
int getCnt(int s, int n) {
int ans = 0;
for (int i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
}
}
C++ 代码:
class Solution {
public:
int minimumXORSum(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), mask = 1 << n, INF = 0x3f3f3f3f;
vector<vector<int>> f(n + 10, vector<int>(mask, INF));
f[0][0] = 0;
auto getCnt = [&](int s, int n) {
int ans = 0;
for (int i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
};
for (int i = 1; i <= n; i++) {
for (int s = 0; s < mask; s++) {
if (getCnt(s, n) != i) continue;
for (int j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) == 0) continue;
f[i][s] = min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
}
};
Python 代码:
class Solution:
def minimumXORSum(self, nums1: List[int], nums2: List[int]) -> int:
n, mask, INF = len(nums1), 1 << len(nums1), 0x3f3f3f3f
f = [[INF] * mask for _ in range(n + 10)]
f[0][0] = 0
for i in range(1, n + 1):
for s in range(mask):
if sum([1 for i in range(n) if (s >> i) & 1]) != i:
continue
for j in range(1, n + 1):
if ((s >> (j - 1)) & 1) == 0:
continue
f[i][s] = min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]))
return f[n][mask - 1]
TypeScript 代码:
function minimumXORSum(nums1: number[], nums2: number[]): number {
const n = nums1.length, mask = 1 << n, INF = 0x3f3f3f3f;
const f: number[][] = new Array(n + 10).fill([]).map(() => new Array(mask).fill(INF));
f[0][0] = 0;
const getCnt = (s: number, n: number): number => {
let ans = 0;
for (let i = 0; i < n; i++) ans += (s >> i) & 1;
return ans;
};
for (let i = 1; i <= n; i++) {
for (let s = 0; s < mask; s++) {
if (getCnt(s, n) !== i) continue;
for (let j = 1; j <= n; j++) {
if (((s >> (j - 1)) & 1) === 0) continue;
f[i][s] = Math.min(f[i][s], f[i - 1][s ^ (1 << (j - 1))] + (nums1[i - 1] ^ nums2[j - 1]));
}
}
}
return f[n][mask - 1];
};
-
时间复杂度: -
空间复杂度:
模拟退火
事实上,这道题还能使用「模拟退火」进行求解。
由于我们可以无限次对 nums2 进行打乱互换,先来思考如何衡量一个 nums2 排列的“好坏”。
一个简单的方式:固定计算 (nums1[0] XOR nums2[0]) + (nums1[1] XOR nums2[1]) + ... + (nums1[n - 1] XOR nums2[n - 1]) 作为衡量当前 nums2 的得分,得分越小,当前的 nums2 排列越好。
迭代开始前先对 nums2 进行一次随机打乱,随后每个回合随机选择 nums2 的两个成员进行互换,并比较互换前后的得分情况,若互换后变好,那么保留该互换操作;若变差,则以一定概率进行重置(重新换回来)。
重复迭代多次,使用一个全局变量 ans 保存下最小异或值之和。
即「模拟退火」的单次迭代基本流程:
-
随机选择两个下标,计算「交换下标元素前对应序列的得分」&「交换下标元素后对应序列的得分」 -
如果温度下降(交换后的序列更优),进入下一次迭代 -
如果温度上升(交换前的序列更优),以「一定的概率」恢复现场(再交换回来)
❝对于一个能够运用模拟退火求解的问题,最核心的是如何实现
❞calc方法(即如何定义一个具体方案的得分),其余均为模板内容。
Java 代码(2024/04/29 可过):
class Solution {
int N = 400;
double hi = 1e5, lo = 1e-5, fa = 0.90;
Random random = new Random(20230823);
void swap(int[] n, int a, int b) {
int c = n[a];
n[a] = n[b];
n[b] = c;
}
int calc() {
int res = 0;
for (int i = 0; i < n; i++) res += n1[i] ^ n2[i];
ans = Math.min(ans, res);
return res;
}
void shuffle(int[] nums) {
for (int i = n; i > 0; i--) swap(nums, random.nextInt(i), i - 1);
}
void sa() {
shuffle(n2);
for (double t = hi; t > lo; t *= fa) {
int a = random.nextInt(n), b = random.nextInt(n);
int prev = calc();
swap(n2, a, b);
int cur = calc();
int diff = cur - prev;
if (Math.log(diff / t) >= random.nextDouble()) swap(n2, a, b);
}
}
int[] n1, n2;
int n;
int ans = Integer.MAX_VALUE;
public int minimumXORSum(int[] nums1, int[] nums2) {
n1 = nums1; n2 = nums2;
n = n1.length;
while (N-- > 0) sa();
return ans;
}
}
-
时间复杂度:启发式搜索不讨论时空复杂度 -
空间复杂度:启发式搜索不讨论时空复杂度
最后
给大伙通知一下 📢 :
全网最低价 LeetCode 会员目前仍可用 ~
📅 年度会员:有效期加赠两个月!!; 季度会员:有效期加赠两周!!
🧧 年度会员:获 66.66 现金红包!!; 季度会员:获 22.22 现金红包!!
🎁 年度会员:参与当月丰厚专属实物抽奖(中奖率 > 30%)!!
专属链接:leetcode.cn/premium/?promoChannel=acoier
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉