从无到有学算法(看漫画学算法)
(๑•̀ㅂ•́)و✧ 爱要坦荡荡 - 萧潇 - 单曲 - 网易云音乐
一,坑爹的奥数
枚举算法又叫穷举算法,非常的暴力,它的基本思想是“有序地去尝试每一种可能”
题目1
□3 x 6528 = 3□ x 8256,在 □ 里填入相同数字使等式成立
#include<iostream>
using namespace std;
int main()
{
for(int i = 1; i <= 9; ++i)
if((i*10+3)*6528 == (30+i) * 8256)
cout<<i<<endl;
return 0;
}
4题目2
□□□ + □□□ = □□□
将数字1 ~ 9分别填入 □ 种,每个数字只能使用一次使等式成立
比如173 + 286 = 459 与 286 + 173 = 459 为一种可能


思路
9个 □ 采用 9 个 for 循环遍历,用 a[i] 表示第 i 个格子地数字,通过book数组标记数字1 ~ 9是否出现过
如果满足每个数字只出现一次,且满足等式,ans++,注意最后输出ans / 2
同时,为避免book[i]累加,每次开始前都要归零
#include<iostream>
using namespace std;
int a[10], book[10];
int main()
{
int i, ans = 0; //可能的情况
for(a[1] = 1; a[1] <= 9; ++a[1])
for(a[2] = 1; a[2] <= 9; ++a[2])
for(a[3] = 1; a[3] <= 9; ++a[3])
for(a[4] = 1; a[4] <= 9; ++a[4])
for(a[5] = 1; a[5] <= 9; ++a[5])
for(a[6] = 1; a[6] <= 9; ++a[6])
for(a[7] = 1; a[7] <= 9; ++a[7])
for(a[8] = 1; a[8] <= 9; ++a[8])
for(a[9] = 1; a[9] <= 9; ++a[9]) { //9个格子,9个for
for(i = 1; i <= 9; ++i)
book[i] = 0;//每次归零
for(i = 1; i <= 9; ++i)
book[a[i]] = 1; //标记是否出现
int sum = 0; //统计不同数字个数
for(i = 1; i<= 9; ++i)
sum += book[i]; //这里不是book[a[i]]
if(sum == 9 && a[1]*100+a[2]*10+a[3] + a[4]*100
+a[5]*10+a[6] == a[7]*100+a[8]*10+a[9]) {
ans++;
cout<<a[1]<<a[2]<<a[3]<<"+"<<a[4]<<a[5]<<a[6]
<<"="<<a[7]<<a[8]<<a[9]<<endl;
}
}
cout<<ans / 2<<endl;
return 0;
}
......(一共336行,所以是168种搭配)
738+216=954
739+125=864
745+218=963
745+236=981
746+235=981
748+215=963
752+184=936
754+182=936
762+183=945
763+182=945
782+154=936
782+163=945
783+162=945
784+152=936
168二,炸弹人


还记得小霸王游戏机上的“炸弹人”吗,用放置炸弹的方法来消灭敌人
炸弹的爆炸方向沿上下左右四个方向
问在哪里放置炸弹可以消灭最多的敌人,已知两种墙,一种可以被炸掉
由于现在只有一枚炸弹,所以墙都用"#"表示(一枚炸弹可以炸掉这种墙,但也会被挡住)
敌人用"G"表示,空地用"."表示,只有空地才能放置炸弹

代码中的x, y表示第x行,第y列,且从第0行第0列开始计算
这里介绍一下走格子的表示方法:
向上 x--,向下 x++,向左 y--,向右 y++
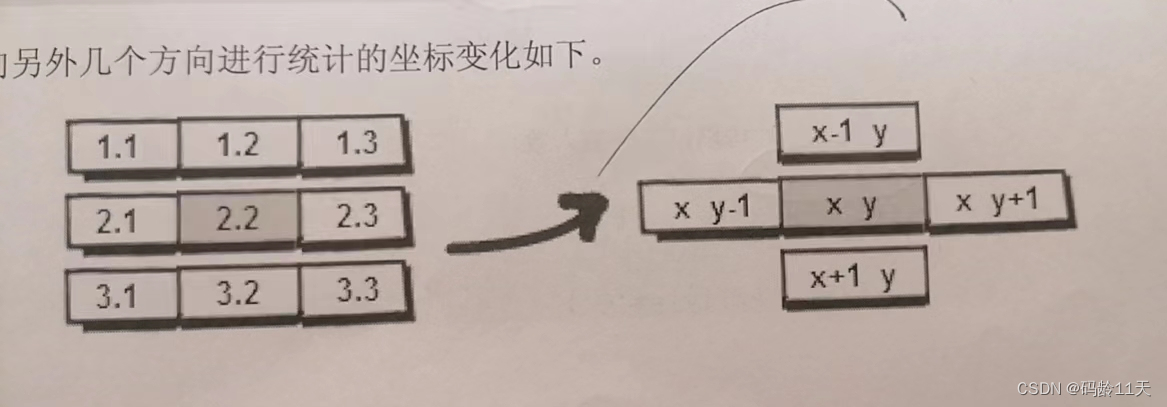
统计每一个空地放置炸弹,可以消灭的总人数(上下左右四个方向敌人个数的和)
#include<iostream>
#include<cstdio> //printf()
using namespace std;
int main()
{
char a[20][20];
int m, n;
cin>>m>>n; //m行,n列
for(int i = 0; i < m; ++i)
cin>>a[i]; //输入m行字符串
int sum, i, j; //每个点消灭敌人个数
int ans = 0, maxi = 0, maxj = 0;
//两个for枚举地图中每个点
for(i = 0; i < m; ++i)
for(j = 0; j < n; ++j) {
if(a[i][j] == '.') {//是空地
sum = 0; //消灭敌人个数
//向上
int x = i, y = j;
while(a[x][y] != '#') {//不是墙
if(a[x][y] == 'G') //遇到敌人
sum++; //消灭
x--; //x--要和if并列
}
//向下
x = i, y = j;
while(a[x][y] != '#') {//不是墙
if(a[x][y] == 'G')
sum++;
x++;
}
//向左
x = i, y = j;
while(a[x][y] != '#') {//不是墙
if(a[x][y] == 'G')
sum++;
y--;
}
//向右
x = i, y = j;
while(a[x][y] != '#') {//不是墙
if(a[x][y] == 'G')
sum++;
y++;
}
if(sum > ans) { //这个if要放在空地的if里
ans = sum; //保留最大值
maxi = i;
maxj = j;
}
}
}
printf("将炸弹放在(%d, %d)处,最多可以消灭%d个敌人",
maxi, maxj, ans);
//i, j要声明在遍历之前,否则输出0,0
return 0;
}
13 13
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.###
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
将炸弹放在(9, 9)处,最多可以消灭8个敌人还有个问题!
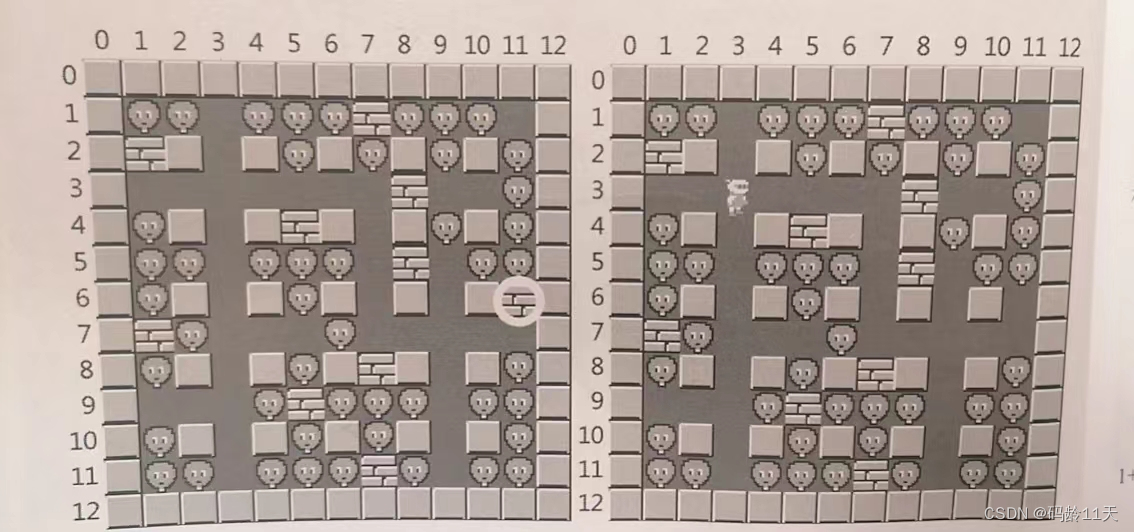
如果将(6, 11)改为平地,小人默认站在(3, 3)这里,根据之前的算法
炸弹放在(1, 11)处,最多可以消灭11个敌人,但小人根本走不到(1, 11)处
13 13
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.#.#
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.#G#
#GG.GGG#G.GG#
#############
将炸弹放在(1, 11)处,最多可以消灭11个敌人正确答案应该是放在(7, 11)处,可以消灭10个敌人,怎么解决这个问题呢?
我会在《啊哈算法》第四章的博客解决这个问题
三,火柴棍等式(NOIP2008提高组)
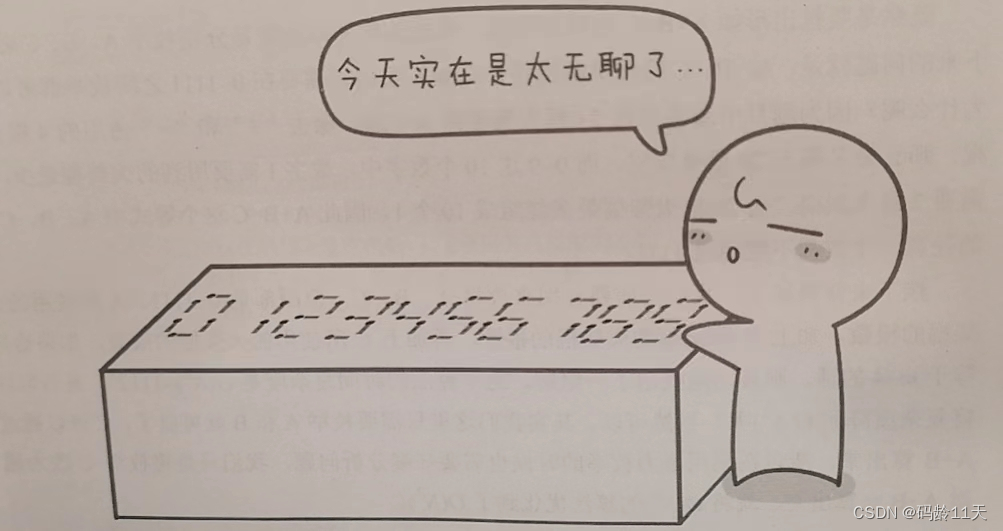
小哼有 n(n <= 24) 根火柴棍,希望拼出形如 A + B = C 的等式,等式种的A,B,C均是用火柴棍拼出的整数(若该数非0,则最高位不为0),数字 1 ~ 9 的拼法如下图所示
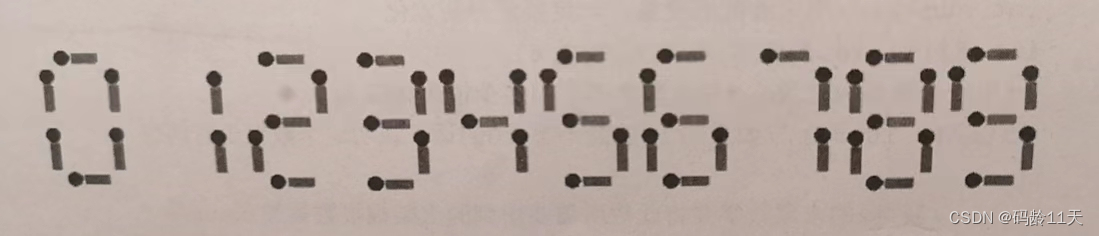
要求:
1,+ 与 = 共需要4根火柴棍
2,如果 A != B,则 A + B = C 与 B + A = C 视为不同等式(A,B,C 都大于 0)
3,所有火柴棍都要用上
注意:
代码第18,19行,为什么遍历到1111呢,因为 n <= 24,除掉 = 和 + 那4跟,还剩20跟
0 ~ 9 中数字 1 需要的火柴棍最少,只需要2根,而20根火柴棍最多组成10个1,所以A,B,C任何一个数都不超过1111
#include<iostream>
using namespace std;
int num(int x) //写个判断火柴数的函数
{
int a[10] = {6,2,5,5,4,5,6,3,7,6}; //单个数字对应的火柴数
int sum = 0; //火柴数
while(x / 10 != 0) {
sum += a[x%10]; //敲重点
x /= 10;
}
sum += a[x]; //此时x为个位数
return sum;
}
int main()
{
int n, c, all = 0;
cin>>n; //总的火柴数
for(int i = 0; i <= 1111; ++i)
for(int j = 0; j <= 1111; ++j) {
c = i + j; //"="右边的数
if(num(i) + num(j) + num(c) == n - 4) {
cout<<i<<"+"<<j<<"="<<c<<endl;
all++;
}
}
cout<<"可以拼出"<<all<<"种不同等式"<<endl;
return 0;
}
18
0+4=4
0+11=11
1+10=11
2+2=4
2+7=9
4+0=4
7+2=9
10+1=11
11+0=11
可以拼出9种不同等式四,数的全排列
这一小节只是为了下一章搜索(dfs等)的引入
123的全排列是123,132,213,231,312,321
1234的全排列是....
123的全排列可以用三重for循环嵌套
1234可以用四重for.....
但如果求123456789的全排列呢,,,
那如果输入n求1 ~ n的全排列呢?比如输入13,求12345678910111213的全排列....
欲知后事如何,且听下回分解(本来打算用随机数做下,感觉半小时写不出来就算了)