随即函数的用处非常大,比如可能用来用做对数器,生成大量随机的测试数据,用来验证我们写的程序是否有误,可以帮助我们快速定位存在错误的测试用例,进行debug。这里注意Java中的随机函数Math.random()是等概率的返回[0,1)区间的任意浮点数
目录
一、将1-5(a-b)的随机函数 转换成 1-7(c-d)的随机函数
一、逻辑分析:
二、代码演示:
二、等概率返回0和1的动态函数
三、等概率返回一个区间内任何数
四、[0,x)范围上的数出现概率由原来的x调整成x平方
五、已知一个函数以不等概率返回0 1,调用其函数得基础上改造成以等概率返回
六、随机函数实现一个对数器,即随机生成大量的测试用例来验证程序是否有错误
结合实际情况,我们对随机函数做一些相应的转换运用
一、将1-5(a-b)的随机函数 转换成 1-7(c-d)的随机函数
一、逻辑分析:
这里需要巧妙用到,二进制位运算得方式来转换,核心就是
- 先将等概率返回1-5的随机函数转换成等概率返回0和1的随即函数。
- 再将0和1随机函数转换为目标函数f(c-c,d-c)的随机函数,如题目标为[1,7]函数,则先转换为[1-1,7-1]即 [0,6]的随机函数,这里就需要用到二进制位运算
- 再将[0,6]等概率随即函数加上目标函数左边界c,题为1,所以得到[1,7]
二、代码演示:
package class02;
public class Code02_RandToRand {
//1.等概率返回[1-5]
public static int f1_5() {
//Math.random()返回[0,1) *5 则为 [0,5) 将其转换int整形则为 [0,4] 再 +1 则为[1-5]
return (int) (Math.random() * 5) + 1;
}
//2.[1-5]转换成等概率返回[0,1]
public static int a() {
int ans = 0;
//核心点就是将1-5 奇数个,需要取偶数个,进行均分到0和1 比如 1 2 输出0, 4 5 输出1,循环3,不为3时则跳出
do {
ans = f1_5();
} while (ans == 3);
return ans > 3 ? 1 : 0;
}
//3.[0,1]转换成等概率返回[0-6]
public static int f0_6() {
int ans = 0;
do {
/*
用二进制位运算来处理, 6 -> 110, 需要取三位,每一位都需要等概率返回0或1,然后会存在111 ->7 ,
不在范围内所以需要进行循环7 不为7时则跳出
*/
ans = (a() << 2) + (a() << 1) + a();
} while (ans == 7);
return ans;
}
//4.[0-6]转换成等概率返回[1-7]
public static int f1_7() {
return f0_6() + 1;
}
public static void main(String[] args) {
System.out.println("测试开始");
// Math.random() -> double -> [0,1)
// 随机函数等概率返回[0,1)证明
int testTimes = 10000000;
int count = 0;
for (int i = 0; i < testTimes; i++) {
if (Math.random() < 0.75) {
count++;
}
}
//验证:随即函数是等概率的返回一个数,小于0.75的数,概率出现的占比就约等同与0.75
System.out.println((double) count / (double) testTimes);
System.out.println("=========");
//验证:等概率[1-5]转换成等概率[1-7] 定义长度8数组 下标是0-7 才能给1-7存数值
int N = 8;
int counts[] = new int[N];
for(int i = 0; i < testTimes; i++){
int num = f1_7();
counts[num]++;
}
for(int i = 1; i < N; i++){
System.out.println(i + "这个数,出现了" + counts[i] + "次");
}
}
}
输出如下:
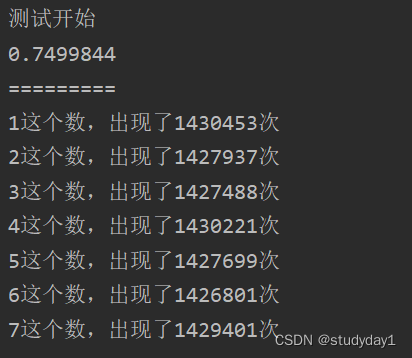
总结:
随机函数返回小于0.75,测验千万次,小于0.75的概率真的就是接近0.75证明等概率
函数F(1-7)等概率返回1-7,也能发现次数都十分接近。
二、等概率返回0和1的动态函数
其实就是跟前面 1-5等概率转换成等概率返回0和1一样,只不过现在是这个区间的未知,动态的。
核心在于将区间转成 [0,max-min] ,其次是要判断是奇数还是偶数,如果是偶数的话,取出区间的个数后除以2得到一个中间值,这个中间值就用来判断[0,max-min] 小于则返回0 大于则返回1,因为个数是偶数个 可以平分,达到等概率,若为奇数,则需要剔除中间值,达到偶数个 ,然后各取两边的数平分给0和1
代码如下:
/*
等概率返回0 1 解决思路:先判断区间个数,如果是奇数,则中间值不能进行输出,1-5,则不输出3 输出12 45 分别表示0 1
然后把区间min-max 转换成 0 - (max-min) 这样再去与求得的区间个数/2的中间值做判断大小返回 0 1
*/
public static int return0_1(int min, int max) {
int size = max - min + 1;
//与1运算可以判断最低位是1还是0 如果是1,表示是奇数, 与1运算后结果为1 ,偶数则最低位位0 ,与1运算后结果为0
boolean flag = (size & 1) != 0;
int ans = 0;
int mid = size / 2;
do {
/*如果是奇数 flag=true,并且ans值等于中间值,就需要进行循环,直到不是中间值跳出 即排除中间值,这样就是偶数个平均0 1概率
例如 13-17 size=17-13+1=5个数 [0,1)*5=[0,5) int -> [0,4] 实际上就是把13-17区间-13 转换成0-4 ,
然后mid=2,也就是0-4的中间值,
*/
ans = (int) (Math.random() * (size));
} while (flag && ans == mid);
return ans > mid ? 1 : 0;
}测试结果如下: 在千万次测试用例 出现0和1的次数很接近

三、等概率返回一个区间内任何数
思路:还是先转换区间,[from,to]区间转换为[0,to-from],最后就是等概率返回[0,to-from]再加上from这个最小值即为题目所求值了。新区间的等概率事件,可以利用上面提到的 用二进制判断需要几位,如1-7 转换为0-6,而6的二进制是110,需要三位二进制,这个上面其实是提到了,因为这里我们具体不清楚需要几位二进制,所以遍历次数num,通过每次左移,然后利用或运算进行累加和,得到ans ,注意就是三位二进制是有111的概率 为7 超过了边界6,所以要排除大于边界值的概率值。
代码如下:
//等概率返回from~to范围上任何一个数 13-17
public static int random(int from, int to) {
if (from == to) {
return from;
}
// 1 ~ 7
// 0 ~ 6
// 0 ~ range
int range = to - from;
int num = 1;
// 求0~range需要几个2进制位 num=3
while ((1 << num) - 1 < range) {
num++;
}
// 我们一共需要num位
// 最终的累加和,首先+0位上是1还是0,1位上是1还是0,2位上是1还是0...
int ans = 0;
do {
ans = 0;
for (int i = 0; i < num; i++) {
//return0_1(from, to) 等概率返回0 1,然后一步步开始左移,或运算表示将每次移位后的值加到ans上,一个为1 则得 1,
//超过了range边界则需要进行循环
ans |= (return0_1(from, to) << i);
}
} while (ans > range);
//最后就是把起始值即最小值加上[0,range]区间等概率返回得值
return ans + from;
}测试结果如下: 在千万次测试用例中 等概率出现1-7,次数很接近

四、[0,x)范围上的数出现概率由原来的x调整成x平方
我们知道Math.random()得到的是一个[0-1)区间等概率任意一个浮点数,即[0,..x,1)区间中,[0-x)的概率接近与x,这个前面已经有代码验证,现在想改造,使得返回[0-x)随机数的概率从x调整到x^2,这里核心就是通过调用两次的随机数,然后为了使两次值都是在[0-x)区间的,我们需要用Math.max(Math.random(), Math.random()),只有两次都使在这两个区间内的,最大值得到的才能是[0,x)区间内的,假设一个不在那就是大于等于x,相当于最大值取不到[0,x),而两次取数都需要确保在[0,x)区间,概率就变成平方了。
代码如下:
// 返回[0,1)的一个小数
// 任意的x,x属于[0,1),[0,x)范围上的数出现概率由原来的x调整成x平方
public static double xToXPower2() {
return Math.max(Math.random(), Math.random());
}
public static void main(String[] args) {
System.out.println("测试开始");
// Math.random() -> double -> [0,1)
// 随机函数等概率返回[0,1)证明
int testTimes = 10000000;
int count = 0;
double x = 0.17;
for (int i = 0; i < testTimes; i++) {
if (xToXPower2() < x) {
count++;
}
}
//验证:[0,x)区间概率从x调整到了x平方
System.out.println((double) count / (double) testTimes);
System.out.println((Math.pow(x, 2)));测试结果如下: 与调用Math.pow()平方函数的值接近
如果要得到[0,x)返回概率x^3呢? 取三次随机数就可以啦。
public static double xToXPower3() {
return Math.max(Math.random(), Math.max(Math.random(), Math.random()));
}
五、已知一个函数以不等概率返回0 1,调用其函数得基础上改造成以等概率返回0 1
假如有个固定函数,不等概率返回0 1,我们也不知道该函数得实现方式,以及以什么不等概率返回,然后通过其函数要转换成等概率的返回 0 1,那我们可以将其调用两次, 如果两次结果相等,那我们就跳过,如果两次结果不一样,那我们就可以返回,表示这次循环两次结果不一样 可以是 0 1 也可能是 1 0 我们就将第一次得到的返回,这样就得到等概率的返回0 1
代码如下:
// 你只能知道,x会以固定概率返回0和1,但是x的内容,你看不到!
public static int x() {
return Math.random() < 0.84 ? 0 : 1;
}
// 等概率返回0和1
public static int y() {
int ans = 0;
do {
//第一次调用得到值,如果条件中第二次调用值与之相等,则继续循环,直到两次是不相等,则返回ans,不等即表示0 1跳出 结果就返回0 或者 1 0跳出,结果就返回1 这两种都是等概率的返回0 1的
ans = x();
} while (ans == x());
return ans;
}
public static void main(String[] args) {
int count0 = 0;
int count1 = 0;
for (int i = 0; i < testTimes; i++) {
if (y() == 0) {
count0++;
}else count1++;
}
System.out.println("0出现次数:" + count0);
System.out.println("1出现次数:" + count1);
}测试结果如下:测试接近
六、随机函数实现一个对数器,即随机生成大量的测试用例来验证程序是否有错误
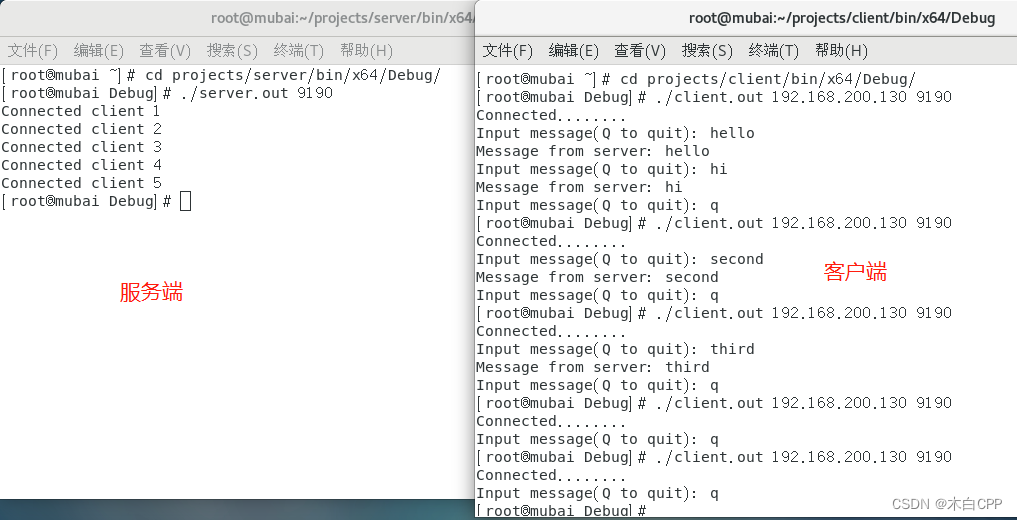
验证选择排序算法是否没有错误,可以定义大量随机用例数组进行传参,另外需要深拷贝一份用例数组,保留原来的顺序。用来判断如果出错了遍历错误的测试用例,两者的长度也肯定是相等的。
代码如下:
package class02;
/**
* 随机函数写一个对数器,即随机生成大量的测试用例来测试程序是否正常
*/
public class Code03_Comp {
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// 返回一个数组arr,arr长度[0,maxLen-1],arr中的每个值[0,maxValue-1]
public static int[] lenRandomValueRandom(int maxLen, int maxValue) {
int len = (int) (Math.random() * maxLen);
int[] ans = new int[len];
for (int i = 0; i < len; i++) {
ans[i] = (int) (Math.random() * maxValue);
}
return ans;
}
public static int[] copyArray(int[] arr) {
int[] ans = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
ans[i] = arr[i];
}
return ans;
}
// arr1和arr2一定等长
public static boolean isSorted(int[] arr) {
if (arr.length < 2) {
return true;
}
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (max > arr[i]) {
return false;
}
max = Math.max(max, arr[i]);
}
return true;
}
public static void main(String[] args) {
int maxLen = 5;
int maxValue = 1000;
int testTime = 10000;
for (int i = 0; i < testTime; i++) {
int[] arr1 = lenRandomValueRandom(maxLen, maxValue);
int[] tmp = copyArray(arr1);
selectionSort(arr1);
if (!isSorted(arr1)) {
for (int j = 0; j < tmp.length; j++) {
System.out.print(tmp[j] + " ");
}
System.out.println();
System.out.println("选择排序错了!");
break;
}
}
}
}






![[Effective Objective] 对象、消息、运行期](https://img-blog.csdnimg.cn/dbc79f87a0f249ed9cb1f0ae69238a4a.png)