前言

本为从地统计学角度，借助空间自相关的方法，从县域尺度，研究江西省各县经济发展水平之间的相关关系，及经济发展与人口之间的相关关系，直观的说明江西省2000年的经济发展状况。通过对各市第一、第二、第三产业的GDP等变量的空间相关性分析，得出江西省各市经济发展之间的空间相互作用以及各个区域内的空间结构特征。

一、研究区概况

江西省全省面积16.69万平方公里，辖11个区市、100个县（市、区），政府驻地（省会）为南昌市。江西处于北回归线附近，春季回暖较早，但天气易变，乍暖乍寒，雨量偏多，直至夏初；盛夏至中秋前晴热干燥；冬季阴冷但霜冻期短，尤其是二十一世纪以来，暖冬气候明显。由于江西地势狭长，南北气候差异较大，但总体来看是春秋季短而夏冬季长。全省气候温暖，日照充足，雨量充沛，无霜期长，为亚热带湿润气候，十分有利于农作物生长。

二、研究数据

全国各县（市）社会经济统计数据（总人口、GDP、第一产业增加值、第二产业增加值、第三产业增加值、第一产业GDP比重、第二产业GDP比重、第三产业GDP比重、财政收入支出、粮食总产量等）。借助ArcGIS软件将江西省各县市数据从全国矢量图中单独提取出来。

各字段对应的属性如下表所示：

四、分析方法

地理数据由于受空间相互作用和空间扩散的影响，彼此之间可能不再相互独立，而是相关的。要研究同一变量在空间分布上的潜在依赖关系，通常采用空间自相关分析的方法。空间自相关(spatial autocorrelation)是指一些变量在同一个分布区内的观测数据之间潜在的相互依赖性。一般来说，空间自相关分析方法在功用上可大致分为两大类：一为全域型（Global Spatial Autocorrelation），另一则为区域型（LocalSpatial Autocorrelation）两种。全局自相关描述某种现象的整体分布情况, 判定区域内是否存在空间集聚特征及集聚强度, 但不能确定集聚的具体位置；局部自相关计算局部空间集聚性并指出集聚的位置, 探测空间异质性。计算空间自相关的方法有许多种，然最为知名也最为常用的有：Moran's I、Geary's C、Getis、Joincount等等，本文主要使用Moran's I指数。

4.1 全局空间自相关指标

（1）Moran's I系数的定义

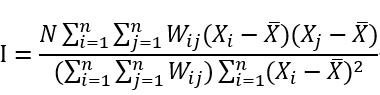
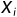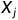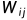式中，N是样本总数， $\text{[math]}$ 、 $\text{[math]}$ 是第i、j个样本的属性值， $\text{[math]}$ 是所有样本属性的平均值， $\text{[math]}$ 是空间权重矩阵。全局Moran's I的值介于-1-1之间，大于0为正相关，且越接近1，正相关性越强, 研究区域内的集聚现象越明显；小于 0为负相关，且越接近- 1，负相关性越强，即邻接空间单元之间具有很强的差异性；接近 0 则表示邻接空间单元不相关。本文通过OpenGeoDa分析江西各县GDP水平的空间关联性。

(2)Moran's I系数的检验

Moran's I 的值可以采用随机分布和正态分布两种假设进行验证，验证的公式为：

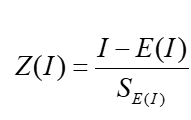
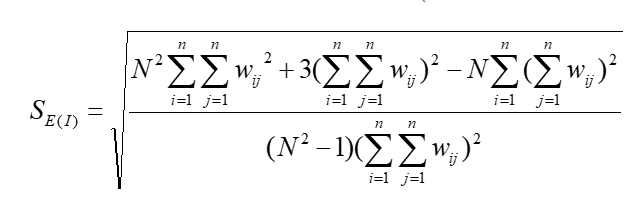
其中I为计算所得Moran's I值，E(I)为理论期望值， $\text{[math]}$ 为理论方差。当Moran's I 为正时，虽可揭示空间上的集聚形态，但不能区分区域内是高值集聚还是低值集聚，故需要研究区域的局部空间自相关。

4.2 局部空间自相关

点往往是空间现象的聚集点，局域自相关可以为局域内每一个空间单元计算一个指标，用来衡量该单元与邻居的关系。局域空间自相关指数形式Local Moran度量区域i与其周围地区空间上的差异程度及其显著性，是全局空间自相关统计量Global Moran's I的分解。对第i个区域而言，其形式为：

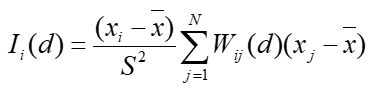
五、分析结果

5.1 确定空间权重矩阵

n个对象之间的空间邻居关系用空间权重矩阵来表示，确定空间权重方法有两种，一是基于空间单元的邻接性，另一种是基于空间单元之间的距离。基于邻接（Contiguity）关系的空间权重有两种原则：一种是Rook原则，认为拥有共同边的多边形邻接；另一种是Queen原则，认为拥有共同边或者共同点的多边形相互邻接。基于距离（Distance）关系的空间权重方法也有两种，一种是ThresholdDistance的原则，即小于某临界距离阈值的单元相关；另一种是K-nearestNeighbors的原则，表示指定某个多边形与周围K个（由用户指定，K=3,4,5,6...）距离最近的多边形相关。

邻接关系权重矩阵取值规则是：

式中: 县域i称为中心县域, 与 i相邻接的所有县域 j都称为相邻县域。

本文采用Rook原则的邻接关系确定权重矩阵，在GeoDa软件中打开jiangxiGDP.shp文件后，Tool->Weights->Create,如下左图对话框中选择Rook后创建的权重矩阵文件打开后如下右图

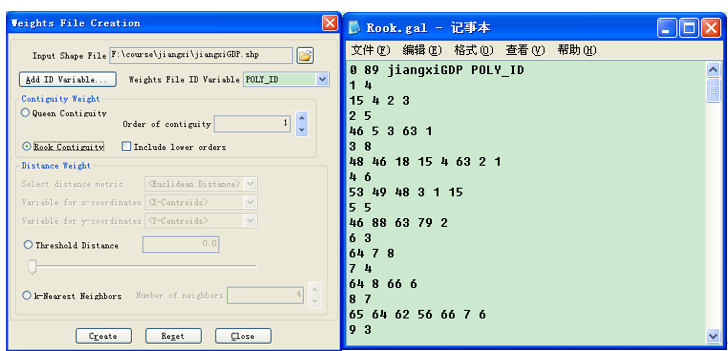
5.2 空间自相关分析

(1) 全局单变量空间自相关

Space->UnivariateMoran's I计算全局单变量空间自相关系数Moran's I，在散点图中右击调用选项菜单选择Randomization->999permutations，利用随机模拟的方法产生直方图，对Moran’s I做显著性检验，得到江西省人口、GDP、第一产业GDP增加值、第二产业GDP增加值、第三产业GDP增加值、第一产业GDP比重、第二产业GDP比重及第三产业GDP比重的Moran's I指数及显著性检验结果如下列图所示：

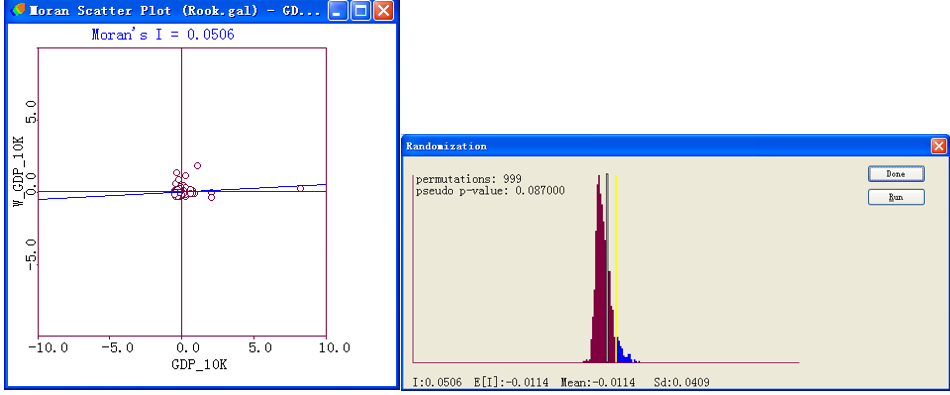
全局单变量空间自相关结果统计表如下：

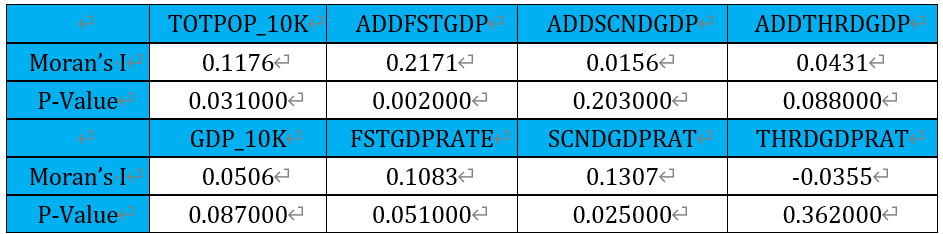
从上述结果可看出：

江西省各县的总人口、GDP、第一产业GDP增加值、第二产业GDP增加值、第三产业GDP增加值、第一产业GDP比重、第二产业GDP比重在空间上邻域间成正相关，第三产业GDP比重的Moran’s I系数为负，邻域间成负相关。

从显著性水平来看，除了GDP，第二产业、第三产业GDP增加值和第三产业GDP比重外，各变量的相关性置信水平都在0.05以上，尤其是第一产业GDP增加值的空间邻域正相关显著，达0.01置信水平。

第一产业GDP增加值明显比第二、第三产业的空间正相关明显，第一产业是指农、林、牧、渔业。第二产业是指采矿业，制造业，电力、燃气及水的生产和供应业，建筑业。

(2) 局域单变量空间自相关

在GeoDa软件中，Space->UnivariateLISA，选择要分析的变量和权重矩阵，在如下对话框中勾选聚集图和显著性图：

生成局域单变量空间自相关的聚集分类和显著性分布图：

第一产业GDP比重的局域空间自相关分析结果

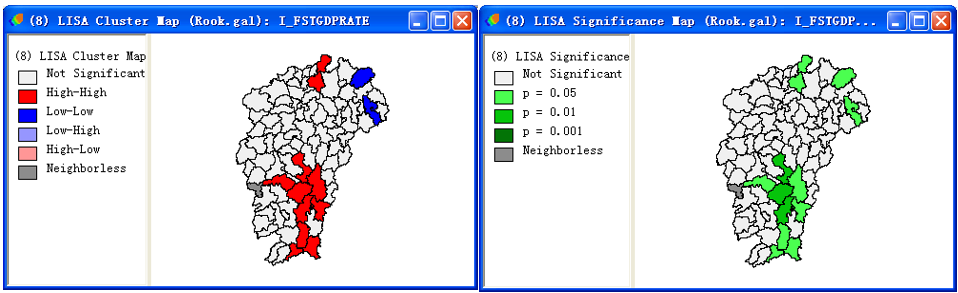
由上图结果可看出，第一产业基本都是邻域正相关，且主要在北部的九江市、上饶市和南部的赣州市聚集。赣州是江西省的一个农业大区和经济作物主产区，现已建成为全国的重点林区和全省的糖业、烟叶、桔等生产基地，著名的赣南脐橙、板鸭等出自这里，因此第一产业在赣州有显著性的高-高聚集。十一届三中全会后上饶市大力发展工业，广丰、玉山工业园被省政府认定为省级重点工业园区，横峰工业园升级为横峰经济开发区，因此第一产业的比重下降，出现了低-低聚集的现象。