本题链接：登录—专业IT笔试面试备考平台_牛客网

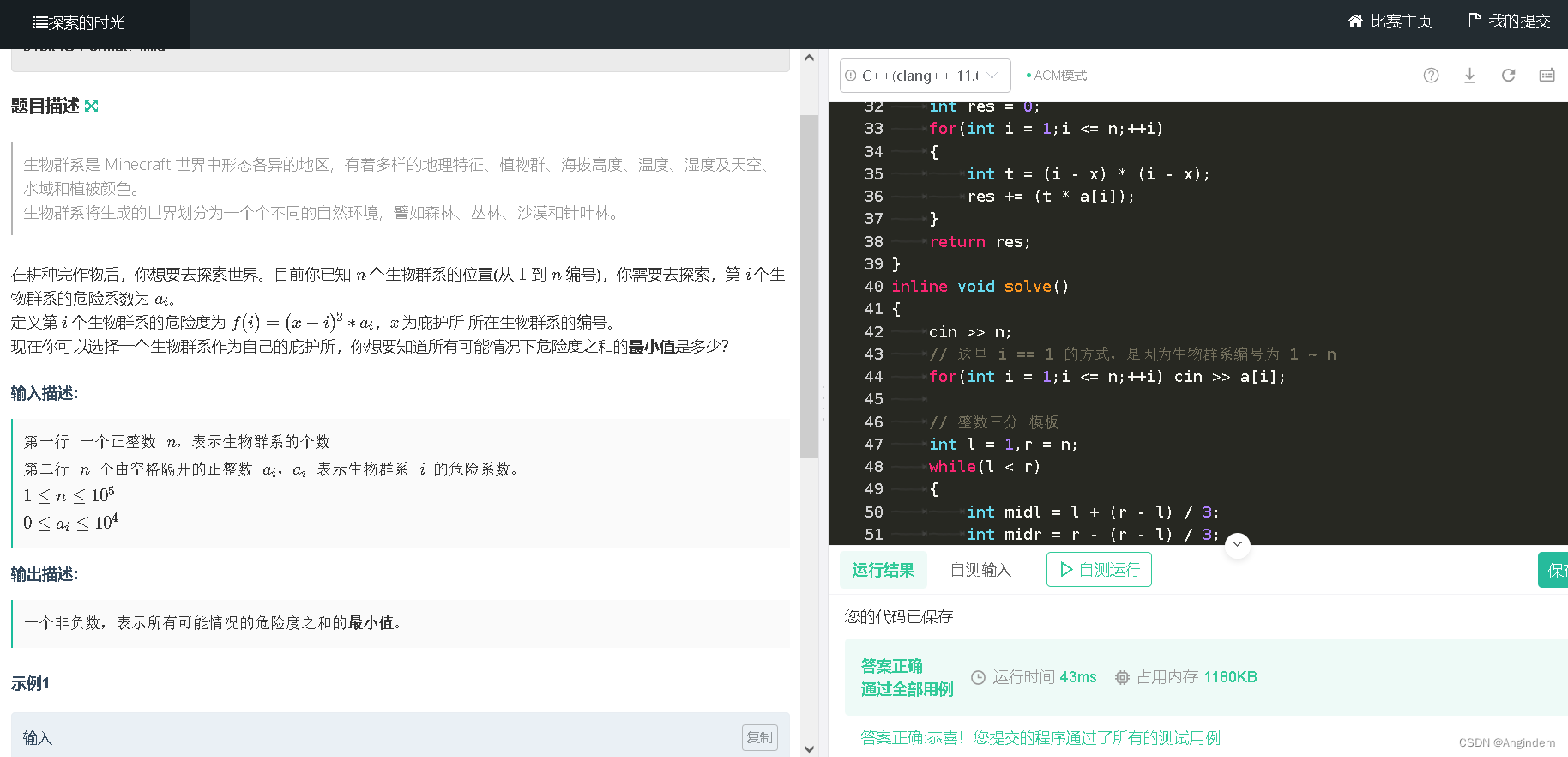
题目：

样例：

5
3 2 1 2 3

思路：

        根据题意，已经给出了运算函数 当我们看到这些函数的时候，联想一下，它们的单调性，以及性质。这是一个抛物线，题目要求我们寻找最小值，说明就是要我们寻找极小值，寻找极值，我们使用三分。

代码详解如下：

#include <iostream>
#include <vector>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define INF 0x3f3f3f3f3f3f
#define umap unordered_map
#define All(x) x.begin(),x.end()
// #pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
inline void solve();

signed main()
{
//	freopen("a.txt", "r", stdin);
	// IOS;
	int _t = 1;
	// cin >> _t;
	while (_t--)
	{
		solve();
	}
	return 0;
}
int n,a[N];
// f 函数性质
inline int f(int x)
{
	int res = 0;
	for(int i = 1;i <= n;++i)
	{
		int t = (i - x) * (i - x);
		res += (t * a[i]);
	}
	return res;
}
inline void solve()
{
	cin >> n;
	// 这里 i == 1 的方式，是因为生物群系编号为 1 ~ n
	for(int i = 1;i <= n;++i) cin >> a[i];
	
	// 整数三分 模板
	int l = 1,r = n;
	while(l < r)
	{
		// r - l 是区间长度， / 3 是分成 3 等份
		int midl = l + (r - l) / 3;
		int midr = r - (r - l) / 3;
		if(f(midl) <= f(midr)) r = midr - 1;
		else l = midl + 1;
	}
	
	int ans = min(f(l),f(r));
	cout << ans << endl;
}

最后提交：