科学计数法

你可能不了解「浮点数」，但你一定了解「科学记数法」。

10进制科学记数法把一个数表示成a与10的n次幂相乘的形式（1≤|a|<10，a不为分数形式，n为整数），例如：

19970000000000 = 1.997 × 10 ^ 13

原本的 19970000000000 表示共需要14位。使用科学计数法后，小数部分 1.997 的表示需要4位，指数部分 13 需要2位，则一共只需要 4+2 = 6 位即可表示这个原本看上去很多很长的数。

小数也可以使用科学计数法来表示，例如：

0.0000001586 = 1.586 × 10 ^ -7

原本的 0.0000001586 表示共需要11位。使用科学计数法后，小数部分 1.586 的表示需要4位，指数部分 -7 需要2位（符号位也占一位），则一共只需要 4+2 = 6 位即可表示该数。

设想我们现在设计了这么一种格式，它表示的是一种10进制的科学计数法。为了说明简单，我们不考虑指数为负数和数值为负数的情况。它一共有8位，每一位都由10进制数字0~9组成，前6位表示小数部分，后2位表示指数部分。例如：

数字 12345603 ，它表示的值是 1.23456 × 10 ^ 3 = 1234.56

数字 12345678 ，它表示的值是 1.23456 × 10 ^ 78 = （一个很大的数）

所以，当我们要表示或运算某个较大或较小且位数较多的数时，用科学记数法会更加方便。

在关于定点数的这篇文章《什么是定点数？》中，我们谈到了什么是「定点数」。简而言之，定点数就是小数点表示固定的数。那么对应的，「浮点数」是不是就是小数点不固定？是浮动的？

恭喜你答对了。

「浮点数」一词，来自英文「float point number」，即「浮动小数点的数」。和上面所说的科学计数法类似，它们的小数点位置都是浮动的。

和10进制的科学计数法一样，2进制数也可以表示成类似的形式，例如：

101.875（D） = 1100101.111（B） = 1.100101111 * 2^6

所以只需要约定好一定的位数来表示小数部分，一定的位数来表示指数部分，就可以完整地表示一个二进制数。如何定义这些细节是个伤脑筋的问题，而且要命的是，如果我定义的标准和同事的标准不一致，那么该听谁的？

好在IEEE（电气与电子工程师协会，Institute of Electrical and Electronics Engineers）帮我们把这些工作都给做了，现在通用的浮点数算术标准是「IEEE 754」。

浮点数格式

IEEE 754 规定了两种常用的浮点数格式：

• 单精度型，也叫32位型，或者float
• 双精度型，也叫64位型，或者double

因为这两种格式的表示规则是类似的，只是位宽不一样，了解了其中一种后，就可以快速掌握另一种，所以下文主要介绍 float 类型的浮点数表示方法。

float类型

float 占用 32 位的存储空间，32 位被分为了如下的三个部分：

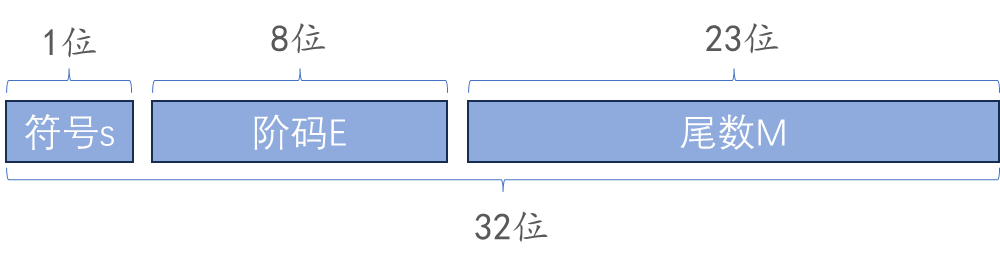
• 符号位s：sign，符号位为 0 说明该浮点数为正数，若为 1 则说明浮点数为负数
• 阶码E：exponent，代表该浮点数被二进制科学表示法规范化后的指数，阶码采用移码表示
• 尾数M：mantissa，被二进制规约化后要求小数点前一位数必须为 1，所以尾数中实际隐含了最高位 1，例如尾数为 M，则实际在还原时，相当于是 1.M

（1）关于尾数M

尾数是用来表示精度的，因为一个数的表示其实是有多种方法的，例如：

314（D） = 3.14 × 10 ^ 2 = 31.4 × 10 ^ 1

1011（B） = 1.011 × 2 ^ 3 = 10.11 × 2 ^ 2 = 101.1 × 2 ^ 1

所以需要对小数部分的表示做出规定，为此标准规定小数部分需要简化到「小数点左边只有一位非0数」的形式。即规定：

314（D） 只能表示为 3.14 × 10 ^ 2 ，而不能表示为 31.4 × 10 ^ 1 或其他形式

1011（B） 只能表示为 1.011 × 2 ^ 3 ，而不能表示为 10.11 × 2 ^ 2，也不能表示为 101.1 × 2 ^ 1 或其他形式

因为10进制的非0数有1~9共9个，所以小数点最左边这位是不能省略掉的；但是2进制数的非0数只有1这个，所以小数点最左边的非0位可以被省略，例如：

1011（B） = 1.011 × 2 ^ 3 ，小数部分虽然为1.011，但是可以省略为.011，即011

这样就可以多表示一位信息。float的尾部部分（即小数部分）定义了23位，因为省略了一个最前面的 1 ，所以它是表示的其实是24位信息。

（2）关于阶码E

阶码是用来表示范围的。float定义了8位数的阶码，所以它的表示范围是0~256（2的256次方）。这种定义有个问题就是无法表示负指数，将其定义为有符号数是个不错的解决办法，但随之而来的问题是–比较两个阶码时不方便。

做两个有符号数的某些运算（例如加法）时，首先需要比较二者的阶码大小，然后对其中一个数的阶码和尾数进行调整。例如：

计算 （3.14 × 10 ^ 2） + （1.56 × 10 ^ 3）的值时，首先需要比较二者的阶码大小，然后对其中一个数进行调整，将（1.56 × 10 ^ 3）重新表示为（15.6 × 10 ^ 2），然后尾数部分相加 3.14 + 15.6 = 15.914，即结果为15.914 × 10 ^ 3，再调整阶码将其规范化，15.914 × 10 ^ 3 = 1.5914 × 10 ^ 4

可以看到，运算其中一个重要的环节就是对两个数的阶码大小进行对比。如果2个阶码是一正一负，那么对比二者的大小还需要考虑符号位，这样就会增加额外逻辑。如果将阶码都加上同一个数，使二者均为正数，那么对比大小就方便很多了。

标准是这样规定的：阶码的值需要加一个偏移量 127 （至于为什么移127不移128，我也不清楚，如果你知道可以告诉我）。例如：

1.011 × 2 ^ 3的原始阶码是3，按规定加上127后等于130，存储到8位空间，即为 1000 0010

光说不练云玩家，接下来看看如何实现浮点数与10进制数之间的转换。

（1）将10进制数转换为float类型的浮点数

将 228 转换为浮点数的流程如下：

1. 是正数，即符号位为0
2. 把10进制转成2进制：228（D）=11100100（B）
3. 写成规范化形式：11100100 = 1.11001 × 2 ^ 7
4. 指数为7，阶码要加上偏移量127，即E = 7 + 127 = 134（D）= 1000 0110（B）
5. 小数部分为1.11001，最前面的1是可以被隐含表示的，所以尾数M = 0.11001 = 11001，因为尾数一共有23位，所以需要在低位补0直到满足位宽要求，即 11001000000000000000000

最终结果为：0 10000110 11001000000000000000000

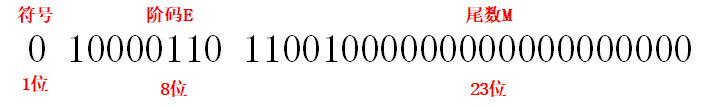
这里有一个浮点数转换网站，可以查询正确结果。

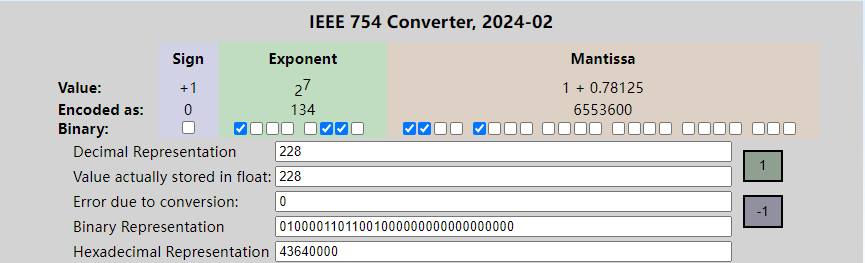
（2）将float类型的浮点数转换为10进制数

将 40490000 （16进制）转换为10进制数的流程如下：

1. 将其转换为2进制，40490000 = 0100 0000 0100 1001 0000 0000 0000 0000，然后分别获取符号、阶码和尾数。
2. 最高位的符号位为0，说明是一个正数
3. 接下来的8位是阶码 10000000（即128），因为加上了偏移量127，所以指数的实际值是128 - 127 = 1。
4. 剩余的23位是尾数10010010000000000000000，即0.1001001，再加上默认的前导1，所以小数部分的值为1+0.1001001 = 1.1001001
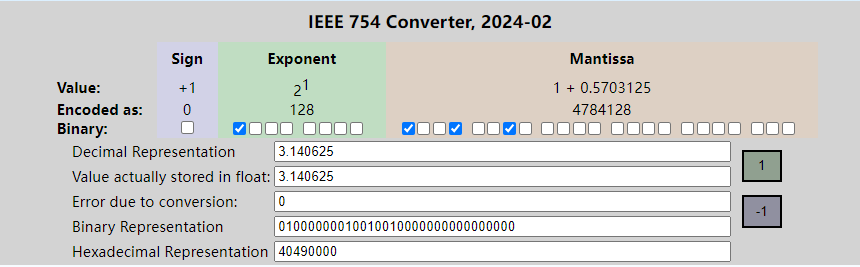
5. 该数的2进制值为 1.1001001 × 2 ^ 1 = 11.001001，将其转化成10进制数11.001001（B）= 3. 140625。（这里的转化有个简便方法，11.001001可以看做是11001001除以2的6次方即64，而11001001也就是201，即201/64 = 3.140625 ）

这是网站转换的结果，和我们换算的结果一致。

double类型

double占用 64 位的存储空间，64 位被分为了如下的三个部分：

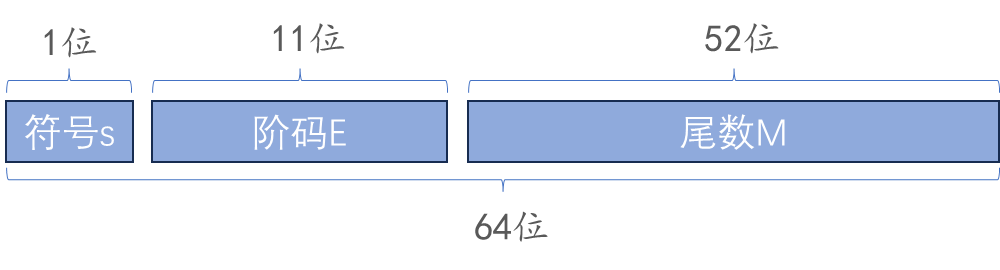
这三部分的定义是和float类型一致的，只是位宽不同。需要注意的是，由于位宽的变化，所以double的阶码的偏移值不再是127，而是 1023。

除了这两种较为常用的类型外，其实IEEE754还规定了几种其他类型，但是都不太常用，所以不赘述了。

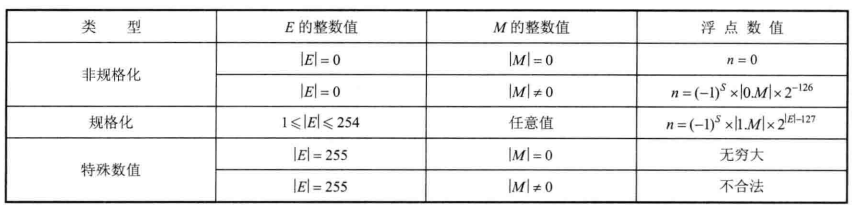
非规约化

当阶码E不全为0，也不全为1时，该浮点数称为**规约化（normal）形式。上面介绍的都是规约化形式的浮点数。当阶码E全为0时，该浮点数称为非规约化（subnormal）**形式。根据尾数的不同，可再分为2种形式：

• 尾数M为全 0 时，表示 0 ，视符号位而定是+0还是-0（二者在某些场景有区别）
• 尾数M不全为 0 时，表示非规约化小数

非规约化小数的定义和规约化小数之间存在如下区别：

• 规约化小数的尾数约定了含有一个隐藏的前导1，也就说真正表示的值是1.xxx；而非规约化小数的尾数则约定含有一个隐藏的前导0，即真正的值为0.xxx。
• 规约化小数的阶码需要加一个偏移量127，而非规约化小数的阶码需要加一个偏移量 126

非规约化小数可以用来表示那些非常小的接近0的数。

特殊值

除此之外，还规定了一些特殊值的表示方法：

• 如果阶码为全1，且尾数为全0时，表示无穷。符号位为0则是正无穷，符号位为1则是负无穷。两个很大的数相乘，或者除以零时，无穷可以表示 溢出 的结果。
• 如果阶码为全1，且尾数不为全0时，为NaN（not a number），表示这不是一个合法实数。一些运算的结果不是合法值，就会返回NaN这样的结果，例如对-1开平方（√-1）

对于以上情况（针对float类型），可以总结如下：