1. 最大似然函数
贝叶斯方法是基于统计理论的一种经典方法,适合于有关参数估计问题。最大似然 (Maximum Likelihood,ML) 估计方法就是贝叶斯估计方法的一种特例,是在已知高斯噪声情况下的贝叶斯最优估计。在ML算法中,观测所得信号的似然函数被定义为含有未知参数的条件概率密度函数,目的是选定未知的参数以使得该似然函数尽可能大。通过最大化似然函数求出的解都被认为是未知参数的一个估计。
给定一个概率分布D,假定其概率密度函数为![]() ,其分布参数为θ。如果不知道θ的值,如何才能估计出θ呢?
,其分布参数为θ。如果不知道θ的值,如何才能估计出θ呢?
一个自然的想法是从这个分布中抽出一个具有n个值的采样![]() ,然后用这些采样数据来估计θ。通过利用贝叶斯方法,可以计算出参数的概率:
,然后用这些采样数据来估计θ。通过利用贝叶斯方法,可以计算出参数的概率:
![]()
最大似然估计的基本思想是,在对被估计的未知量没有任何先验知识的情况下,利用已知的若干观测值估计该参数。其中似然函数是包含位置参数信息的可能性(likelihood)。
满足高斯分布的概率密度函数:
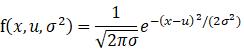
似然函数:
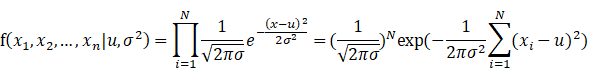
使用Matlab仿真可以如下的结果,峰值对应的索引即是估计值。

2. 确定性最大似然估计概述
在信号处理中,最著名和最常用的建模方法是最大似然法。根据源信号(输入序列)模型假设的不同,基于最大似然的波达方向估计方法分为确定性最大似然算法DML和随机性最大似然算法SML两大类型。随机性最大似然算法也称统计最大似然法。
(1) 确定性最大似然算法:源信号或输入序列{s(k)}假定为确定性信号,待估计的未知参数是输入序列和信道向量,即θ = (h, {s(k)}),虽然可能只对估计信道向量h感兴趣。在这种情况下,未知参数的维数随观测数据量的增多而增大。
(2) 随机性最大似然算法:输入序列{s(k)}假设为一具有已知分布的随机过程(通常假设为高斯随机过程),而且唯一待估计的未知参数就是信道向量即θ = h。在这种情况下,未知参数的维数相对于观测数据量是固定的。
3. 信号模型
假设空间中存在M各不同方向的信号,入射到由N个天线单元构成的均匀直线阵上。
令第m个信号源的方向为θm,对应的信号波形为sm(t)。令第n个天线单元的噪声为nm(t)。那么,在窄带远场条件下,天线阵的接收信号为
![]()
其中,A为阵列流形矩阵,矩阵大小为N*M,具体可表示为M个不同方向对应的阵列导向矢量:
![]()
假设信号模型中的噪声n(t)为圆对称高斯白噪声随机过程,不同阵元的噪声相互独立,信号波形s(t)为确定性信号。
在上述统计假设下,噪声n(t)的一阶矩和二阶矩满足
![]()
![]()
由于源信号是确定性信号,接收信号也服从高斯分布,其一阶矩和二阶矩满足
![]()
![]()
4. 确定性最大似然估计算法
在确定性最大似然算法所采用的数据模型中,背景噪声和接收噪声被认为是大量独立的噪声源发射的,因而把噪声过程视为平稳高斯随机白噪声过程,而信号波形则假设是确定性信号,但输入波形是待估计的未知参数(载波频率假定为已知)。假定空间噪声是白色的和循环对称的,则一个复随机过程称为循环对称的,若它的实部和虚部为同一分布,并有一个反对称的互协方差,即 ![]() ,
,
且噪声项的二阶矩取为
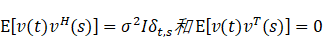
在上述统计假设下,观测向量x(t)也是循环对称的,并且是高斯白色随机过程,其均值为A(θ)s(t),协方差矩阵为σ2I。
似然函数定义为给定未知参数时所有观测值的概率密度函数。令测量向量x(t)的概率密度函数是复变量高斯分布
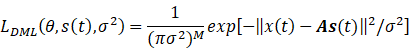
式中,A = A(θ),而M是复变量的个数。由于测量值是独立的,所以似然函数为

如上所述,确定性最大似然算法中的似然函数的未知参数是信号参数θ和噪声方差σ2。这些未知量的最大似然估计由似然函数L(θ, s(t), σ2)的最大变化量给出。为了方便,最大似然估计定义为负对数似然函数-log L(θ, s(t), σ2)的最小变化量。用N归一化,并忽略与未知参数独立的Mlogπ项,即有
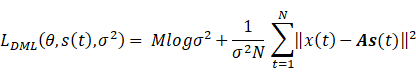
其最小变化量就是确定性最大似然估计值。由文献(Estimation of source parameters by maximum likelihood and nonlinear regression)公式推导可知,相对于σ2和s(t)的显式最小化变量为

![]()
式中,![]() 为样本协方差矩阵;A+是A的伪逆矩阵;
为样本协方差矩阵;A+是A的伪逆矩阵;![]() 是
是![]() 零空间上的正交投影矩阵。即
零空间上的正交投影矩阵。即


将上述公式代入后可以证明,信号参数θ的确定性最大似然估计是下列最小化问题的解,即

这是因为测量向量x(t)投影到与所有期望信号分量正交的模型空间上,x(t)在此模型空间的功率测量值为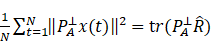 。显然,当投影把所有真实的信号分量都出去时,即当θ=θ0时,能量应该为最小。由于只有有限个噪声样本可利用,所以能量不能被准确测量,
。显然,当投影把所有真实的信号分量都出去时,即当θ=θ0时,能量应该为最小。由于只有有限个噪声样本可利用,所以能量不能被准确测量,![]() 将偏离θ0。然而,如果是平稳情况,当样本个数趋于无穷大时,误差将收敛为零。这一结果对相关信号甚至相干信号也成立。
将偏离θ0。然而,如果是平稳情况,当样本个数趋于无穷大时,误差将收敛为零。这一结果对相关信号甚至相干信号也成立。
为了计算确定性最大似然估计,在数值上必须求解非线性多维优化问题。必要时,还可以求出信号波形和噪声方差的估计值。如果有一个很好的初始值,则高斯牛顿法将能迅速收敛到似然函数的极小值。然而,获得一个足够精确的初始估计值通常是很困难的。若初始值差,那么搜索方法便可能收敛到局部极小值。
5.DML测角仿真
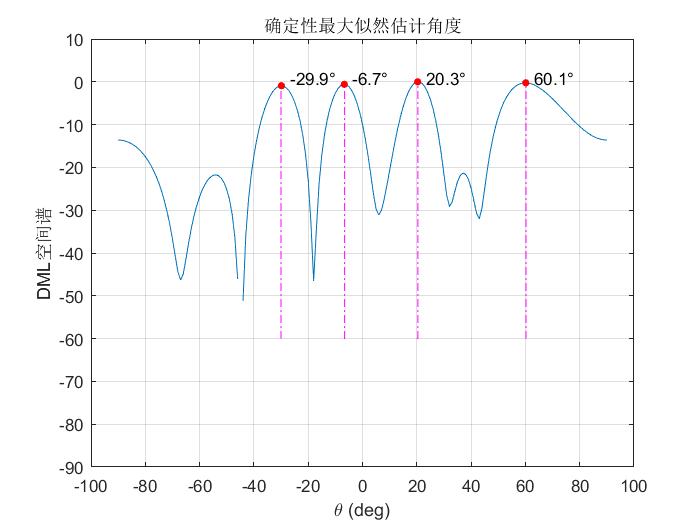
根据上述模型和公式,假设均匀线性阵列,则DML对角度遍历搜索可以得到角度谱,峰值即是入射角。

如果使用牛顿迭代法,可以在角度上先做粗略搜索,在用牛顿法迭代搜索峰值,仿真结果如下。
6.参考资料
张贤达,现代信号处理
张小飞,阵列信号处理及MATLAB实现
基于确定性最大似然算法 DML 的 DoA 估计,用牛顿法实现(附 MATLAB 源码)_基于最大似然的doa估计程序-CSDN博客