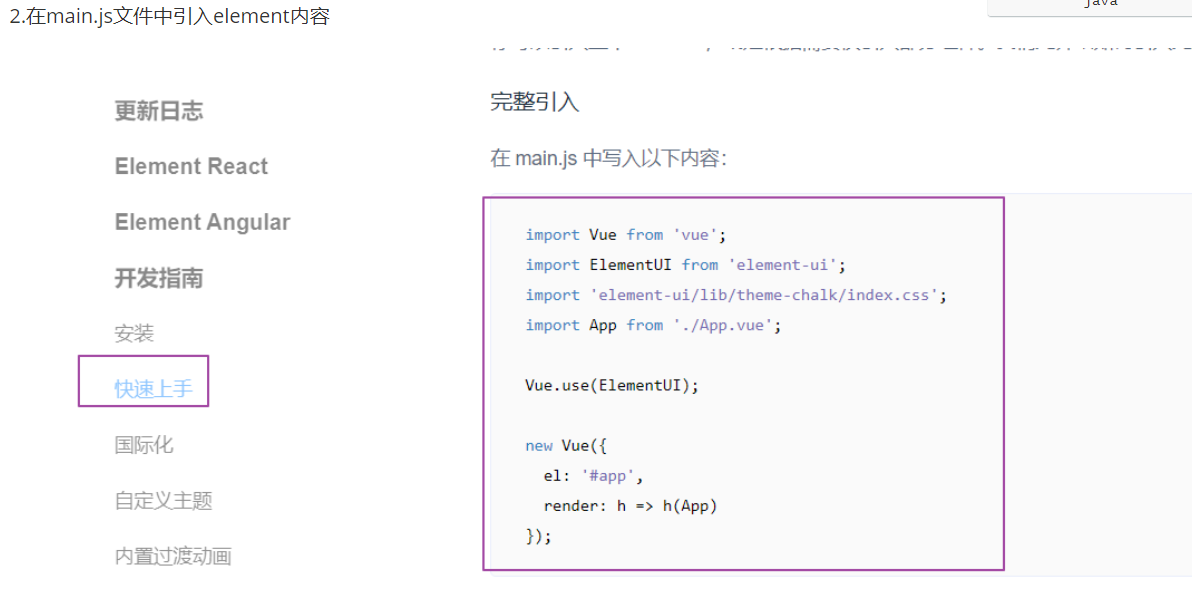
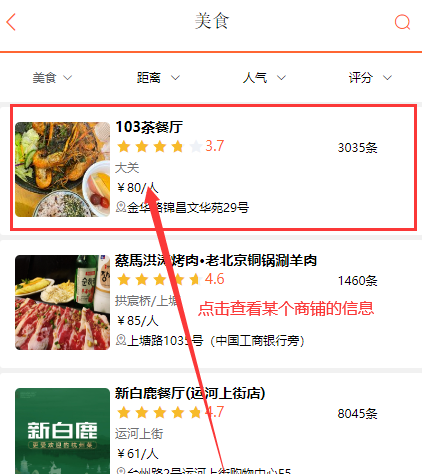
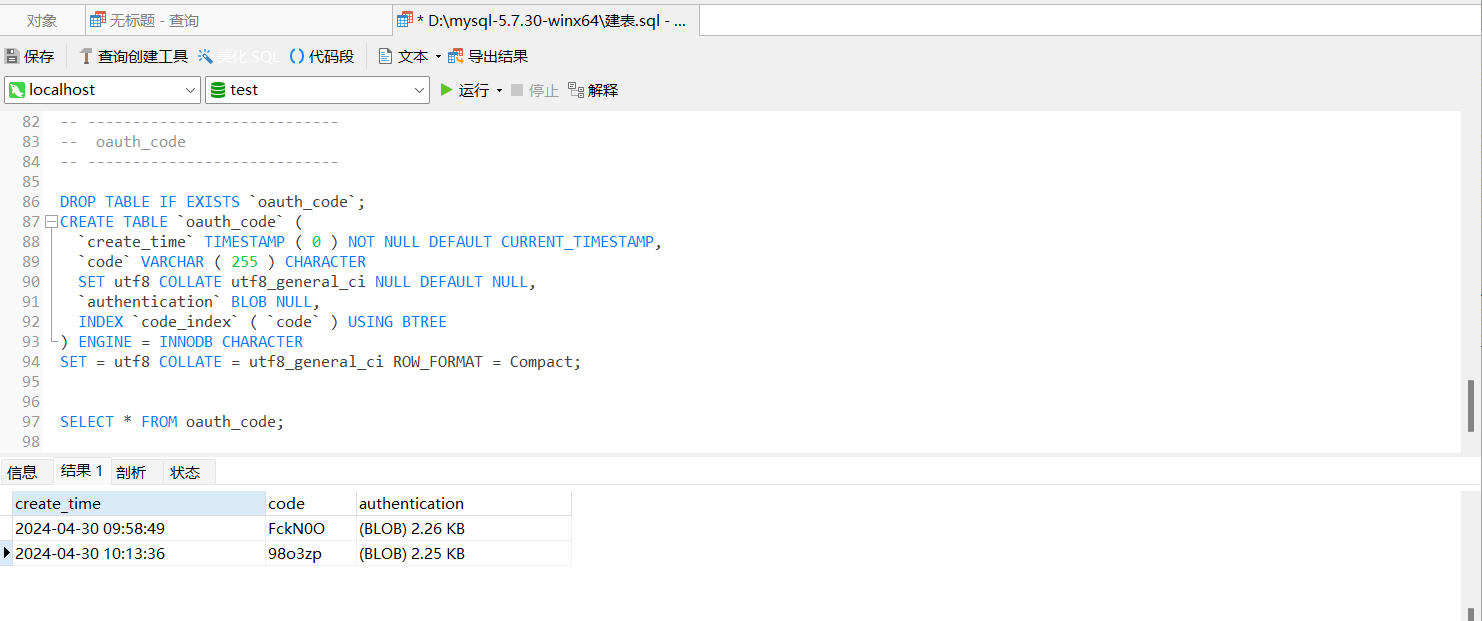
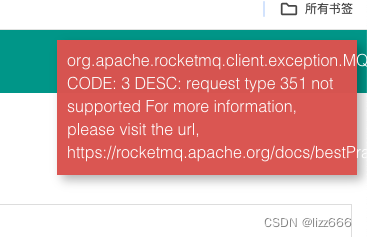
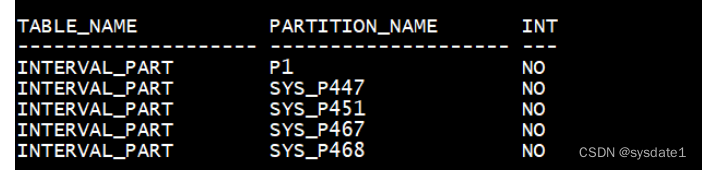
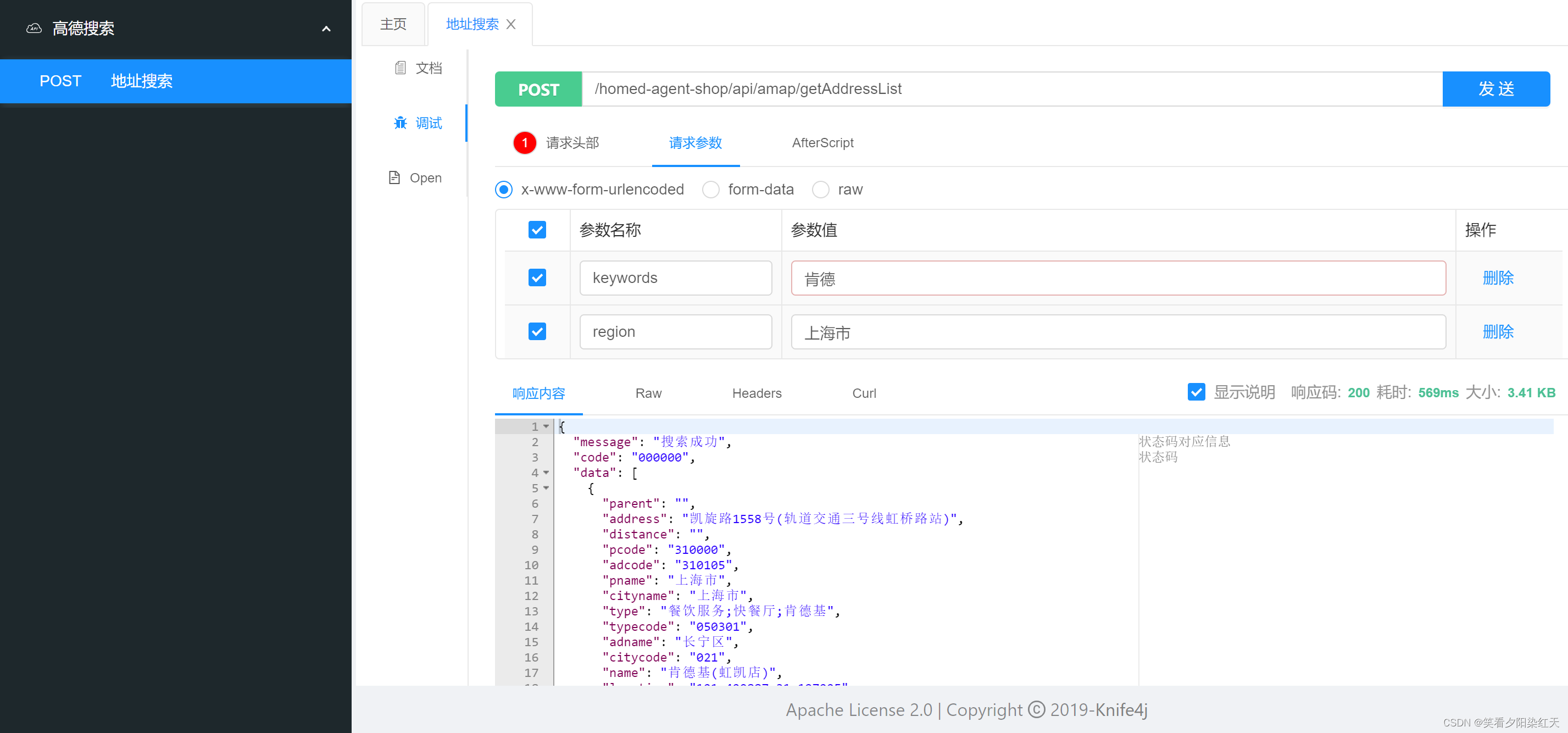
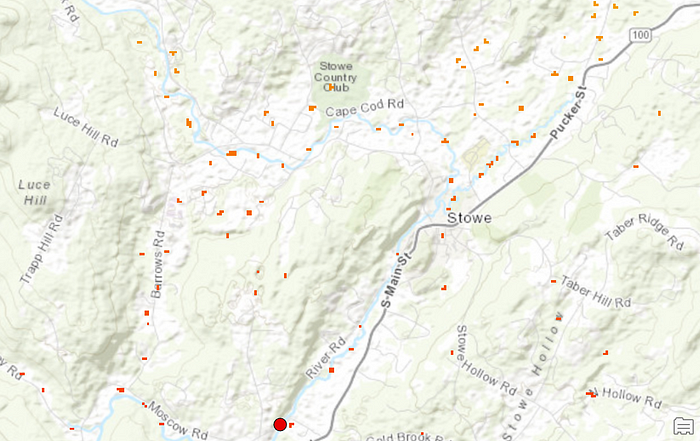
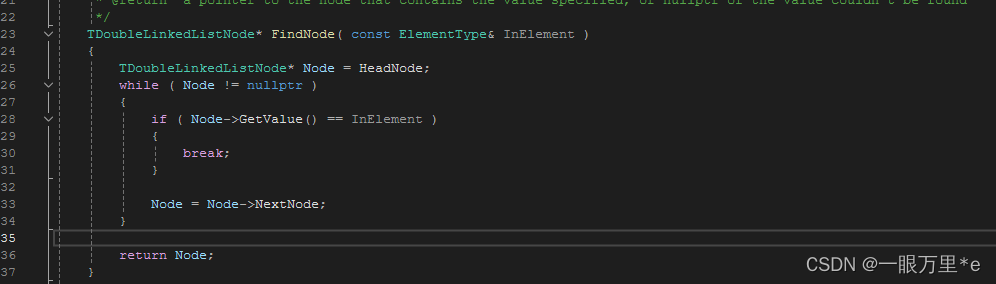
从左至右依次为托马斯·贝叶斯、皮埃尔-西蒙·拉普拉斯和哈罗德·杰弗里斯——逆概率(即现在所说的客观贝叶斯分析)发展中的关键人物。[24]

历史背景

1654年，帕斯卡尔和费马共同解决了“点问题”, 创造了早期的直接概率推理理论。三十年后，雅各布·伯努利将概率理论扩展到了归纳推理。伯努利指出，在现实中，为了预先枚举所有可能性来确定“哪一种可能性更大”是徒劳的。

例如，他提到，我们难以枚举所有可能侵袭人类的疾病并决定其杀死人的概率的相对大小。因此他提出了通过观察类似案例来从后验角度获取概率的方法。

伯努利推理出，前进的方法是从后验概率中获得：

Here, however, another way for attaining the desired is really opening for us. And, what we are not given to derive a priori, we at least can obtain a posteriori, that is, can extract it from a repeated observation of the results of similar examples. [2, p. 18]

为了证明这种方法的有效性，伯努利证明了二项分布的一个大数定律版本。设 X_n 表示参数 r/t（二者为整数）的伯努利分布样本。如果 c 是某个正整数，则伯努利展示出，对于足够大的 N 来说：

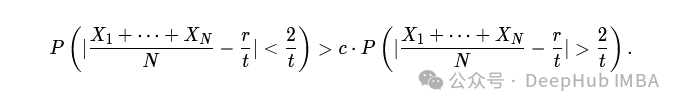
换句话说，来自二项分布的样本比率在 (r−1)/t 到 (r+1)/t 的概率至少比在此范围外的概率高出 c 倍。所以通过获取足够多的样本，我们“几乎能像预先知道参数一样从后验中确定参数”。

伯努利还推导出给定 r 和 t 的情况下，为达到特定准确度所需的样本数量。比如，若 r=30 且 t=50，他展示出：

having made 25550 experiments, it will be more than a thousand times more likely that the ratio of the number of obtained fertile observations to their total number is contained within the limits 31/50 and 29/50 rather than beyond them [2, p. 30]

这种方法虽然提供了推理途径，但在几方面有所不足：

1. 它的界限取决于已知参数，无法量化未知参数的不确定性。
2. 达到高置信度所需的实验数量过多，限制了实用性。

德·莫瓦尔在他的《The Doctrine of Chances》中改进了伯努利的工作，推导出更紧凑的界限，但仍未提供在参数未知时量化不确定性的方式，仅给出了这样的定性指导：

if after taking a great number of Experiments, it should be perceived that the happenings and failings have been nearly in a certain proportion, such as of 2 to 1, it may safely be concluded that the Probabilities of happening or failing at any one time assigned will be very near that proportion, and that the greater the number of Experiments has been, so much nearer the Truth will the conjectures be that are derived from them. [3, p. 242]

贝叶斯推理的崛起

受莫瓦尔著作的启发，托马斯·贝叶斯开始研究二项分布的推理问题。他重新设定了目标

Given the number of times in which an unknown event has happened and failed: Required the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named. [4, p. 4]

他认识到，解决方案取决于先验概率，并试图解决

the case of an event concerning the probability of which we absolutely know nothing antecedently to any trials made concerning it [4, p. 11]

贝叶斯提出，没有任何信息相当于均匀先验分布[5, p. 184–188]。通过均匀先验和几何类比，他成功近似了后验分布的积分。

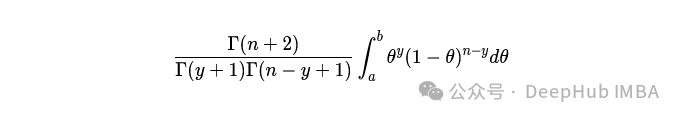
并能回答问题，如“若观察到某二项分布的 y 次成功和 n−y 次失败，参数 θ 在 a 和 b 之间的概率是多少”。

尽管贝叶斯成功解决了推理问题，但他的工作并未得到广泛采用。他的论文在1763年被出版，但直到德·摩根50多年后才引起注意。数学史学家斯蒂格勒提到：

Bayes essay ’Towards solving a problem in the doctrine of chances’ is extremely difficult to read today–even when we know what to look for. [5, p. 179]

拉普拉斯的推进

贝叶斯去世十年后，可能对贝叶斯的发现并不知情，拉普拉斯也致力于类似问题，并独立采取了相同的方法。他重新审视了著名的点数问题，这次考虑了技能游戏的情况，将玩家获胜概率建模为带有未知参数 p 的伯努利分布。拉普拉斯也选择了均匀先验，仅指出：

because the probability that A will win a point is unknown, we may suppose it to be any unspecified number whatever between 0 and 1. [6]

与贝叶斯不同的是，拉普拉斯没有使用几何方法，而是采用更完善的分析工具，推导出更实用的公式和更清晰的符号。

接下来，直到20世纪初，均匀先验结合贝叶斯定理成为统计推理的流行方法。1837年，德·摩根引入了逆概率一词来描述这些方法，并承认贝叶斯的早期工作：

De Moivre, nevertheless, did not discover the inverse method. This was first used by the Rev. T. Bayes, in Phil. Trans. liii. 370.; and the author, though now almost forgotten, deserves the most honourable rememberance from all who read the history of this science. [7, p. vii

逆概率的批评

20世纪初，逆概率因其使用均匀先验而受到严重攻击。罗纳德·费舍尔是其中一位激烈的批评者，他写道：

I know only one case in mathematics of a doctrine which has been accepted and developed by the most eminent men of their time, and is now perhaps accepted by men now living, which at the same time has appeared to a succession of sound writers to be fundamentally false and devoid of foundation. Yet that is quite exactly the position in respect of inverse probability [8]

费舍尔批评逆概率“极度武断”，并指出了均匀先验在不同尺度下产生的不同结果。他提供了一个例子：

让 p 表示二项分布的未知参数。

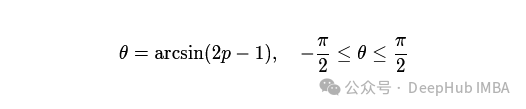
并应用均匀先验。那么观察到S成功和F失败后θ在a和b之间的概率是

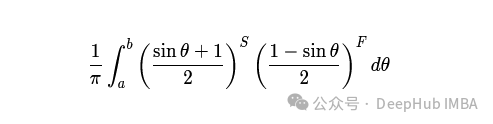
把变量变回p就等于

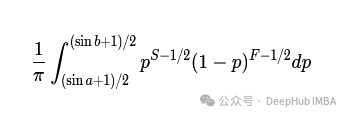
因此，θ 的均匀先验等价于 p 上的 1/π p^{−1/2} (1 − p)^{−1/2}。作为替代，费舍尔提倡最大似然方法、p值以及频率学派的概率定义。

客观贝叶斯分析的推进

尽管费舍尔等人主张放弃逆概率，但哈罗德·杰弗里斯努力巩固其基础。他提出了基于费舍尔信息矩阵的先验分布，并且也关注结果的参数独立性问题：

frequentist definitions themselves lead to no results of the kind that we need until the notion of reasonable degree of belief is reintroduced, and that since the whole purpose of these definitions is to avoid this notion they necessarily fail in their object. [10, p. 34]

杰弗里斯指出，逆概率不必与均匀先验联系在一起:

There is no more need for [the idea that the uniform distribution ofthe prior probability was a necessary part of the principle of inverse probability] than there is to say that an oven that has once cooked roast beef can never cook anything but roast beef. [10, p. 103]

为了在重新参数化下获得一致的结果，杰弗里斯提出了基于费舍尔信息矩阵的先验，

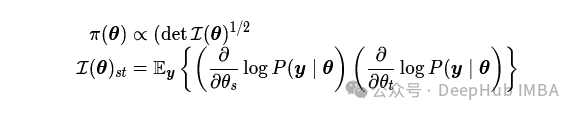
若Θ表示参数空间的一个区域，φ(u)是一个内射连续函数，其值域包括Θ，则应用变量变换公式可得

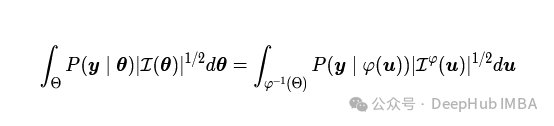
后来，Welch 和 Peers 通过研究后验分布中的单尾可信区间来评估先验的频率匹配性能。并指出 Jeffreys 提出的先验在单参数模型中是渐近最优的，为先验提供了进一步的理由，这与直觉表明我们可以量化Bayes“绝对一无所知”的标准相一致。

但是主流统计学忽略了杰弗里斯的方法，而去追求看似客观的频率学派方法：

In my experience teaching many academic physicians, when physicians are presented with a single-sentence summary of a study that produced a surprising result with P = 0.05, the overwhelming majority will confidently state that there is a 95% or greater chance that the null hypothesis is incorrect. [12]

贝杰和塞尔克则证明了这种误解如何导致严重错误：

it is shown that actual evidence against a null (as measured, say, by posterior probability or comparative likelihood) can differ by an order of magnitude from the P value. For instance, data that yield a P value of .05, when testing a normal mean, result in a posterior probability of the null of at least .30 for any objective prior distribution. [15]

他们总结到

for testing “precise” hypotheses, p values should not be used directly, because they are too easily misinterpreted. The standard approach in teaching–of stressing the formal definition of a p value while warning against its misinterpretation–has simply been an abysmal failure. [16]

上面就是对贝叶斯推理发展的历史背景总结，我们将进一步探讨如何通过匹配覆盖率来证明客观贝叶斯分析的先验;重新审视贝叶斯和拉普拉斯研究过的问题，看看如何用更现代的方法来解决这些问题。

先验和频率匹配

匹配先验的想法直觉上与我们在缺乏先验知识的情况下如何思考概率是一致的。我们可以把频率覆盖匹配指标看作是回答“给定先验分布的贝叶斯可信区间有多准确?”这个问题的一种方式。

让我们考虑一个单参数概率模型，参数为 θ。假如我们有一个先验分布 π(θ)，如何测试该先验是否合理地表达了贝叶斯所要求的“无知”？

我们可以选择一个样本量 n 和一个真实值 θtrue，然后随机从分布 P(· |θtrue) 中采样观测值 y = (y1, … , yn)^T。然后，我们计算包含后验分布95%概率质量的双尾可信区间 [θa, θb]，并记录该区间是否包含 θtrue。然后我们重复实验，改变 n 和 θtrue，观察 π(θ) 的覆盖性能。

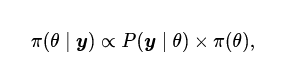
如果 π(θ) 是一个好的先验，那么θ_true 被可信区间包含的次数会稳定在95%附近。

我们可以这样用算法来表达这个实验:

 function coverage-test(n, θ_true, α):
   cnt ← 0
   N ← a large number
   for i ← 1 to N do
     y ← sample from P(·|θ_true)
     t ← integrate_{-∞}^θ_true π(θ | y)dθ
     if (1 - α)/2 < t < 1 - (1 - α)/2:
       cnt ← cnt + 1
     end if
   end for
   return cnt / N

1、均值未知的正态分布

假设我们观察到n个正态分布值y，方差为1，均值为μ，未知。让我们考虑一下先验

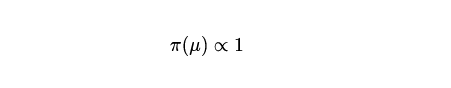
然后

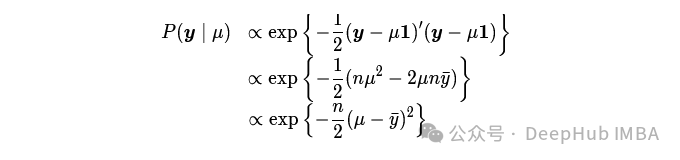
所以

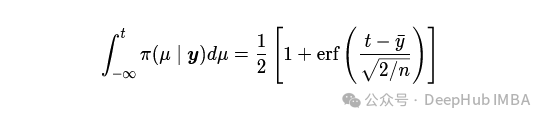
我用10000次试验和不同的μ和n值进行了95%覆盖率的测试，如下表所示，结果都接近95%，表明常数先验在这种情况下是一个很好的选择。

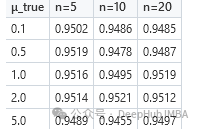
2、方差未知的正态分布

现在假设我们观察到n个正态分布的值y，方差未知，均值为零。我们来测试一下常数先验和杰弗里先验，

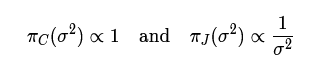
我们就得到

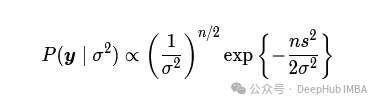
s²=y’y/n. 带入 u=ns²/(2σ²).

得到

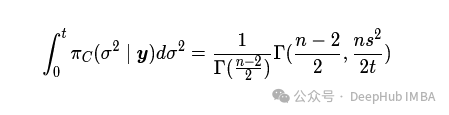
最总化简得到

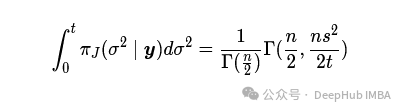
下表显示了具有恒定先验的95%覆盖率测试的结果。我们可以看到，对于较小的n值，覆盖率明显小于95%。

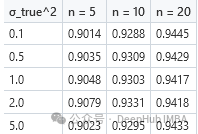
相比之下，如果我们使用杰弗里斯先验，所有n值的覆盖率始终接近95%。

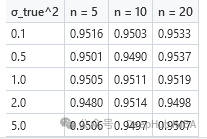
二项分布先验

我们将杰弗里的逆概率方法应用到二项分布中。

假设我们从二项分布中观察到n个值。设y表示成功的次数，θ表示成功的概率。似然函数为

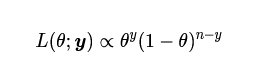
取对数求导，得到

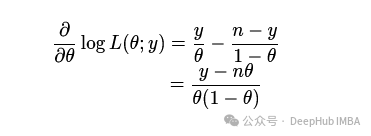
因此，二项分布的Fisher信息矩阵为

杰弗里的先验是

对比

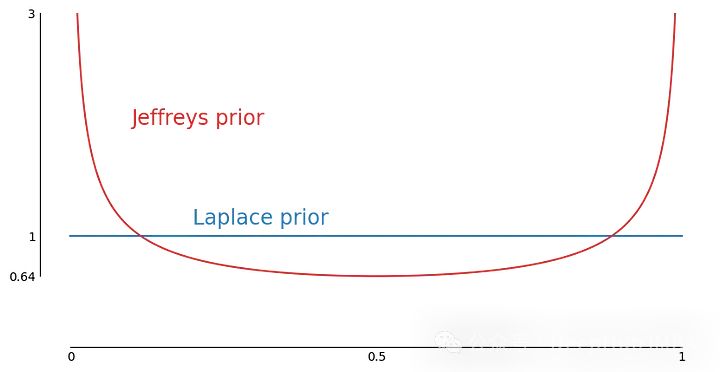
然后是后验

我们可以把它看作参数为y+1/2和n-y+1/2的分布。为了测试频率主义者的覆盖率，我们可以使用一个精确的算法。

 function binomial-coverage-test(n, θ_true, α):
   cov ← 0
   for y ← 0 to n do
     t ← integrate_0^θ_true π(θ | y)dθ
     if (1 - α)/2 < t < 1 - (1 - α)/2:
       cov ← cov + binomial_coefficient(n, y) * θ_true^y * (1 - θ_true)^(n-y)
     end if
   end for
   return cov

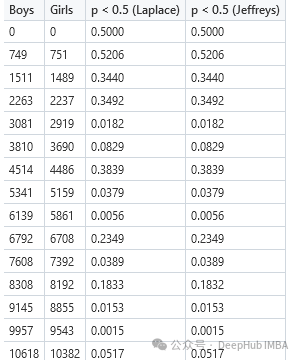
下面是使用贝叶斯-拉普拉斯均匀先验对α=0.95和p、n的不同值的覆盖结果:

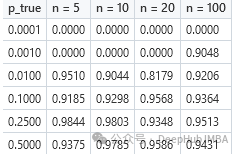
使用杰弗里斯先验的覆盖结果:

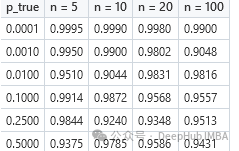
我们可以看到，许多表项的覆盖率是相同的。但是，对于较小的n和p_true值，杰弗里先验提供了不错的结果。

贝叶斯和拉普拉斯的应用

现在让我们回顾一下贝叶斯和拉普拉斯研究过的一些应用。考虑到所有这些问题的目标都是为参数空间的一个区间分配一个概率，我们可以强有力地证明，杰弗里斯先验比均匀先验更好，因为它在渐进上具有最佳的频率覆盖性能。这也解决了费舍尔关于任意性的批评。

彩票问题

中奖几率未知的彩票

Let us then imagine a person present at the drawing of a lottery, who knows nothing of its scheme or of the proportion of Blanks to Prizes in it. Let it further be supposed, that he is obliged to infer this from the number of blanks he hears drawn compared with the number of prizes; and that it is enquired what conclusions in these circumstances he may reasonably make. [4, p. 19–20]

他问了一个具体的问题:

Let him first hear ten blanks drawn and one prize, and let it be enquired what chance he will have for being right if he gussses that the proportion of blanks to prizes in the lottery lies somewhere between the proportions of 9 to 1 and 11 to 1. [4, p. 20]

用贝叶斯先验和θ表示抽到空白的概率，我们得到了后验分布

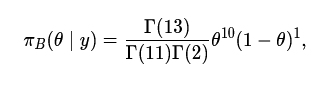
答案

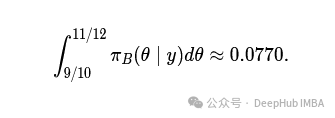
利用杰弗里斯先验，我们得到后验

答案是

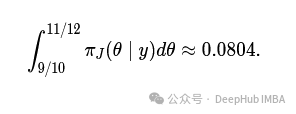
然后Price考虑同样的问题(θ在9/10和11/12之间的概率是多少)，在不同的情况下，一个彩票观察者看到w个中奖和10w个空。下面我展示了使用贝叶斯均匀先验和杰弗里斯先验对不同w值的后验概率。

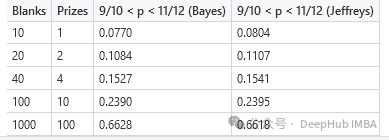
出生率

现在让我们转向一个令拉普拉斯和他的同时代人着迷的问题:男孩对女孩的相对出生率。拉普拉斯引入了这个问题，

The consideration of the [influence of past events on the probability of future events] leads me to speak of births: as this matter is one of the most interesting in which we are able to apply the Calculus of probabilities, I manage so to treat with all care owing to its importance, by determining what is, in this case, the influence of the observed events on those which must take place, and how, by its multiplying, they uncover for us the true ratio of the possibilities of the births of a boy and of a girl. [18, p. 1]

和贝叶斯一样，拉普拉斯用均匀先验来解决问题，写

When we have nothing given a priori on the possibility of an event, it is necessary to assume all the possibilities, from zero to unity, equally probable; thus, observation can alone instruct us on the ratio of the births of boys and of girls, we must, considering the thing only in itself and setting aside the events, to assume the law of possibility of the births of a boy or of a girl constant from zero to unity, and to start from this hypothesis into the different problems that we can propose on this object. [18, p. 26]

拉普拉斯利用1745年至1770年间巴黎的数据，其中251527个男孩和241945个女孩出生，他问道，“出生一个男孩的可能性等于或小于1/2的概率是多少”?

有了均匀先验，B = 251527, G = 241945， θ表示男孩出生的概率，我们就得到了后验

答案是

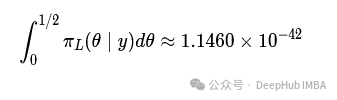
对于杰弗里先验，我们同样推导出后验

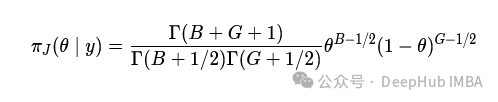
答案是

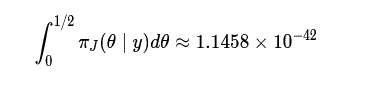
下面是一些使用p_true = B / (B + G)的模拟数据，显示了随着观察到更多的新生儿，答案可能会如何演变。

一些观点和讨论

1、贝叶斯分析在统计学中的地位

我认为杰弗里斯是正确的，标准统计程序应该提供“我们需要的结果”。虽然贝叶斯和拉普拉斯在选择均匀先验方面可能并非完全合理，但他们在以可信度量化结果的目标上是正确的。杰弗里斯概述的方法（后来的参考先验）为我们提供了一条路径，可以提供“我们需要的结果”，同时解决了均匀先验的任意性。杰弗里斯的方法不是获得可信程度结果的唯一途径，如果情况允许，更主观的方法也可以有效，但他的方法为我们提供了在“我们对概率一无所知的事件”情况下的良好答案，并且可以作为频率学方法的直接替代品。

更具体地说，我认为，当你翻开一本标准的统计学入门教材，查找如关于方差未知的正态分布数据的均值是否为非零的假设检验等基本程序时，你应该看到基于客观先验和贝叶斯因子的方法【19】，而不是基于P值的方法。

2、在没有先验知识的情况下，不是有多种方法来推导出好的先验吗？

本文强调了频率覆盖匹配作为评估先验是否是客观分析的良好候选的基准，但覆盖匹配并不是我们可以使用的唯一有效指标，并且可能有多种具有良好覆盖率的先验可以推导出来。不同的具有良好频率性质的先验可能会相似，任何结果都将更多地由观察数据而非先验决定。如果我们处于多种良好先验导致显著不同结果的情况下，那么这表明我们需要提供主观输入来得到有用的答案。以下是伯杰对此问题的回答：

Inventing a new criterion for finding “the optimal objective prior” has proven to be a popular research pastime, and the result is that many competing priors are now available for many situations. This multiplicity can be bewildering to the casual user.

I have found the reference prior approach to be the most successful approach, sometimes complemented by invariance considerations as well as study of frequentist properties of resulting procedures. Through such considerations, a particular prior usually emerges as the clear winner in many scenarios, and can be put forth as the recommended objective prior for the situation. [20]

3、这难道不会使逆概率变得主观，而频率学方法提供了统计学的客观方法吗？

认为频率学方法是客观的，这是一个常见的误解。伯杰和贝里提供了一个示例来证明这一点【21】：假设我们观察一个研究人员研究硬币偏见的研究。我们看到研究人员将硬币抛了17次。正面出现了13次，反面出现了4次。假设θ代表正面出现的概率，而研究人员正在进行一个标准P值测试，其零假设是硬币没有偏见，θ=0.5。他们会得到什么P值？我们无法回答这个问题，因为研究人员会根据他们的实验意图而得到显著不同的结果。

如果研究人员打算抛硬币17次，那么在零假设下看到正面次数少于13次的概率可以通过汇总代表获得5到12次正面的二项分布项来得到。

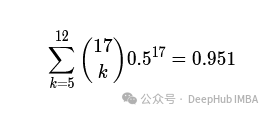
p值为1-0.951 =0.049。

如果研究人员打算继续投掷，直到他们得到至少4次正面和4次反面，那么在零假设下，看到一个值小于17次的概率是由负二项分布项求和给出的，这些负二项分布项表示得到8到16次投掷的概率，

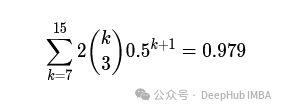
p值为1-0.979 =0.021

结果不仅取决于数据，还取决于研究人员隐藏的意图。正如伯杰和贝瑞所言，“统计学通常不可能做到客观……标准的统计方法可能会产生误导性的推论。”

4、如果主观性是不可避免的，那为什么不直接使用主观先验？

在有主观意见的情况下，我们应该纳入主观意见。但我们也应该承认，贝叶斯的“关于我们完全不知道其概率的事件”是一个重要的推理基本问题，需要很好的解决方案。正如埃德温·詹斯所写

To reject the question, [how do we find the prior representing “complete ignorance”?], as some have done, on the grounds that the state of complete ignorance does not “exist” would be just as absurd as to reject Euclidean geometry on the grounds that a physical point does not exist. In the study of inductive inference, the notion of complete ignorance intrudes itself into the theory just as naturally and inevitably as the concept of zero in arithmetic.

If one rejects the consideration of complete ignorance on the grounds that the notion is vague and ill-defined, the reply is that the notion cannot be evaded in any full theory of inference. So if it is still ill-defined, then a major and immediate objective must be to find a precise definition which will agree with intuitive requirements and be of constructive use in a mathematical theory. [22]

此外，像参考先验这样的系统方法肯定比伪贝叶斯技术做得更好，比如在截断的参数空间上选择一个均匀的先验，或者在一个看起来很有趣的参数空间区域上选择一个模糊的适当先验，比如高斯先验。即使主观信息是可用的，使用参考先验作为构建块通常是整合它的最佳方法。如果我们知道一个参数被限制在一个特定的范围内，但不知道更多，我们可以简单地通过限制和重新规范化它来适应先前的引用[14,p. 256]。

总结

对统计结果(如P值或置信区间)的常见和反复的误解表明，我们有一种强烈的自然倾向，想要根据逆概率来思考推理。难怪这种方法统治了150年。

Fisher和其他人批评幼稚地使用统一先验是武断的，这当然是正确的，但这在很大程度上是通过参考先验和采用频率匹配覆盖等指标来解决的，这些指标量化了先验代表无知的意义。正如伯杰所说，

We would argue that noninformative prior Bayesian analysis is the single most powerful method of statistical analysis, in the sense of being the ad hoc method most likely to yield a sensible answer for a given investment of effort. And the answers so obtained have the added feature of being, in some sense, the most “objective” statistical answers obtainable [23, p. 90]

本文引用

[1]: Problem of the points: Suppose two players A and B each contribute an equal amount of money into a prize pot. A and B then agree to play repeated rounds of a game of chance, with the players having an equal probability of winning any round, until one of the players has won k rounds. The player that first reaches k wins takes the entirety of the prize pot. Now, suppose the game is interrupted with neither player reaching k wins. If A has w_A wins and B has w_B wins, what’s a fair way to split the pot?

[2]: Bernoulli, J. (1713). On the Law of Large Numbers, Part Four of Ars Conjectandi. Translated by Oscar Sheynin.

[3]: De Moivre, A. (1756). The Doctrine of Chances.

[4]: Bayes, T. (1763). An essay towards solving a problem in the doctrine of chances. by the late rev. mr. bayes, f. r. s. communicated by mr. price, in a letter to john canton, a. m. f. r. s. Philosophical Transactions of the Royal Society of London 53, 370–418.

[5]: Stigler, S. (1990). The History of Statistics: The Measurement of Uncer- tainty before 1900. Belknap Press.

[6]: Laplace, P. (1774). Memoir on the probability of the causes of events. Translated by S. M. Stigler.

[7]: De Morgan, A. (1838). An Essay On Probabilities: And On Their Application To Life Contingencies And Insurance Offices.

[8]: Fisher, R. (1930). Inverse probability. Mathematical Proceedings of the Cambridge Philosophical Society 26(4), 528–535.

[9]: Fisher, R. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 222, 309–368.

[10]: Jeffreys, H. (1961). Theory of Probability (3 ed.). Oxford Classic Texts in the Physical Sciences.

[11]: Welch, B. L. and H. W. Peers (1963). On formulae for confidence points based on integrals of weighted likelihoods. Journal of the Royal Statistical Society Series B-methodological 25, 318–329.

[12]: Goodman, S. (1999, June). Toward evidence-based medical statistics. 1: The p value fallacy. Annals of Internal Medicine 130 (12), 995–1004.

[13]: Berger, J. O., J. M. Bernardo, and D. Sun (2009). The formal definition of reference priors. The Annals of Statistics 37 (2), 905–938.

[14]: Berger, J., J. Bernardo, and D. Sun (2024). Objective Bayesian Inference. World Scientific.

[15]: Berger, J. and T. Sellke (1987). Testing a point null hypothesis: The irreconcilability of p values and evidence. Journal of the American Statistical Association 82(397), 112–22.

[16]: Selke, T., M. J. Bayarri, and J. Berger (2001). Calibration of p values for testing precise null hypotheses. The American Statistician 855(1), 62–71.

[17]: Berger, J., J. Bernardo, and D. Sun (2022). Objective bayesian inference and its relationship to frequentism.

[18]: Laplace, P. (1778). Mémoire sur les probabilités. Translated by Richard J. Pulskamp.

[19]: Berger, J. and J. Mortera (1999). Default bayes factors for nonnested hypothesis testing. Journal of the American Statistical Association 94 (446), 542–554.

[20]: Berger, J. (2006). The case for objective Bayesian analysis. Bayesian Analysis 1(3), 385–402.

[21]: Berger, J. O. and D. A. Berry (1988). Statistical analysis and the illusion of objectivity. American Scientist 76(2), 159–165.

[22]: Jaynes, E. T. (1968). Prior probabilities. Ieee Transactions on Systems and Cybernetics (3), 227–241.

[23]: Berger, J. (1985). Statistical Decision Theory and Bayesian Analysis. Springer.

[24]: The portrait of Thomas Bayes is in the public domain; the portrait of Pierre-Simon Laplace is by Johann Ernst Heinsius (1775) and licensed under Creative Commons Attribution-Share Alike 4.0 International; and use of Harold Jeffreys portrait qualifies for fair use.

[25]: Zabell, S. (1989). R. A. Fisher on the History of Inverse Probability. Statistical Science 4(3), 247–256.

https://avoid.overfit.cn/post/8c7a66d96347413db8925c5d02e5ecf0

作者：Ryan Burn