前言

还是惯例来感慨一下，transforemr是google公司在2017年7月发表的【Attention Is All You Need】这篇文章中被提出来的。而在大模型得到了蓬勃发展的今天，不管是哪一类大模型（视频、图像、文本），基本上模型的基础架构都是采用了transformer或者是transformer的变体。这一定程度上奠定了transformer的铁王座地位。
惊讶的是这个时代红利的最大受益者不是那些开发LLM的公司，而是英伟达，老黄都笑嘻了，为此老黄还特意在2024年的GTC大会上邀请了transformer的7位创作者。以表transformer给他带来这破天富贵。
好的，闲话就吹到这，下面开始进入正题。

动机

因为transformer最开始主要是为了解决NLP相关的问题，所以我们首先得了解一下NLP任务大概有啥特点。

NLP任务特点

在NLP领域有不同的任务：诸如情感分类、多项选择、机器翻译等，但是不管什么任务，他们都是和文本打交道，所以最重要的基础工作就是要充分学习到文本中每一个词的信息。而文本的特点就在于词语与词之间是有关联的。举一个例子吧：

你真的很狗阿

这里的“狗”其实是需要结合着最开始的“你”来进行分析的。而不能独立分析。
ok了，总结一下NLP任务的特点在于：文本中词与词之间是有关联的。

循环神经网络

循环神经网络流行原因

上一小节我们知道了NLP任务特点在于：文本中词与词之间是有很大关联的，这就意味着你如果要想解决好NLP任务，在学习每一个词的信息的时候，就要充分考虑其周边的其他词（上下文），因为他们之间会有似有若无的联系。而就是因为这一个特点，给传统的神经网络下了死刑，因为传统神经网络输入的特征与特征之间是没有联系，模型在输入的时候一般都是独立的去考虑问题。自然就不能充分捕获每一个词的信息了，自然对于上层的情感分类等任务自然效果就不会那么好了。而这也就是RNN系列（LSTM、GRU等）兴起的原因，因为RNN网络结构的特殊性，导致在学习某个词的信息的时候，就会充分考虑过去时刻出现的词的信息。这不就契合了NLP任务的特点了嘛。所以在Transformer没出现之前，RNN系列算是统治了NLP领域了。关于RNN的详细内容，我在之前还写过一片博客，感兴趣可以去看看：从RNN到LSTM

循环神经网络缺点

虽然RNN系列在学习词的信息的时候也充分考虑到了过去时刻的每一个词的信息，但是因为它计算原理的特点，导致它出现了一些难以处理的缺点：

1. 处理长序列文本很困难，很难充分捕获长文本的信息，例如句尾的词很难充分考虑到句头出现词的信息；
2. 无法并行计算，因为后一个时刻是依赖前一时刻的结果，自然就无法并行计算了；
3. 训练时间长，且训练难以收敛，这是因为rnn在学习下一个时刻出现的词的信息的时候是需要考虑前一时刻出现的词的信息的，而前一个时刻出现的词又依赖前前时刻的信息了，这就成了一个递归了。而递归你可以简单的理解为它就类似一个深度的神经网络，而网络加深，自然训练时间就会变长，同时在反向梯度计算的时候，容易出现梯度弥散，自然难以收敛。

所以这就给了Transformer来革命的机会，Transformer也会一一的解决RNN系列的这些缺点。

transformer架构

整体架构（编码器-解码器）

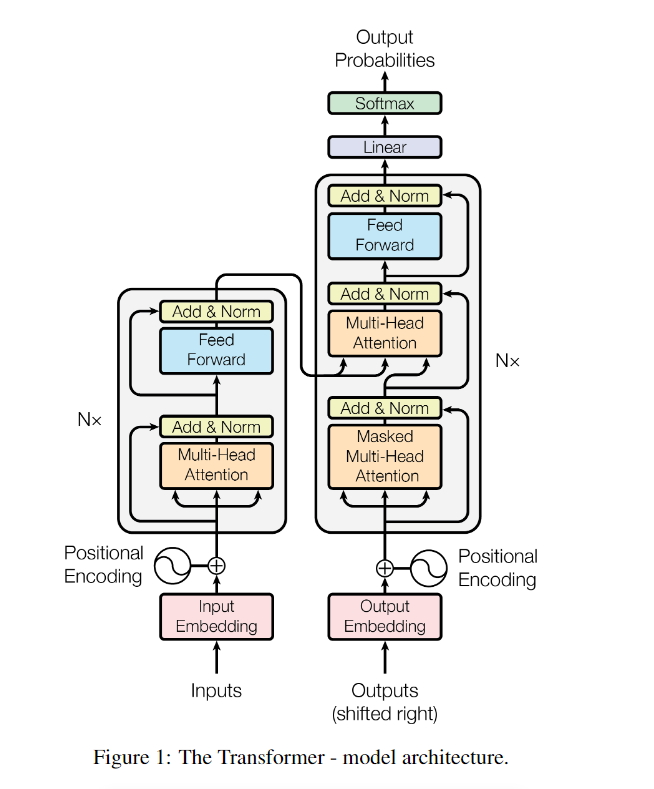
上一节介绍了，截止Transformer之前，RNN系列基本上已经统治了NLP领域了，基本上NLP的任务都会基于循环神经网络或者它的变体去做，但是又不单纯的用循环神经网络，而是基于循环神经网络去架构一个encoder-decoder模型，尤其是在机器翻译领域。而过往的事实证明这个encoder-decoder架构在文本翻译、摘要总结等的任务上都实现了sota。所以Transformer也秉承了这一点，整体上采用encoder-decoder结构。只是这个encoder-decoder结构下的原子结构不是rnn，而是self-attention(自注意力)+前馈神经网络。下面是原论文的模型结构，左侧是编码器、右侧是解码器，后面我们会逐个来讲解这个架构内容。

自注意力（self-attention）

因为transformer是基于自注意力机制架构的，所以就要先了解自注意力。下面我们一步步引出这个结构。我们还是以句子：你真的很狗阿,这句话的学习为例。

传统NLP解决方案

在传统的神经网络中，大致的解决方案如下图所示：

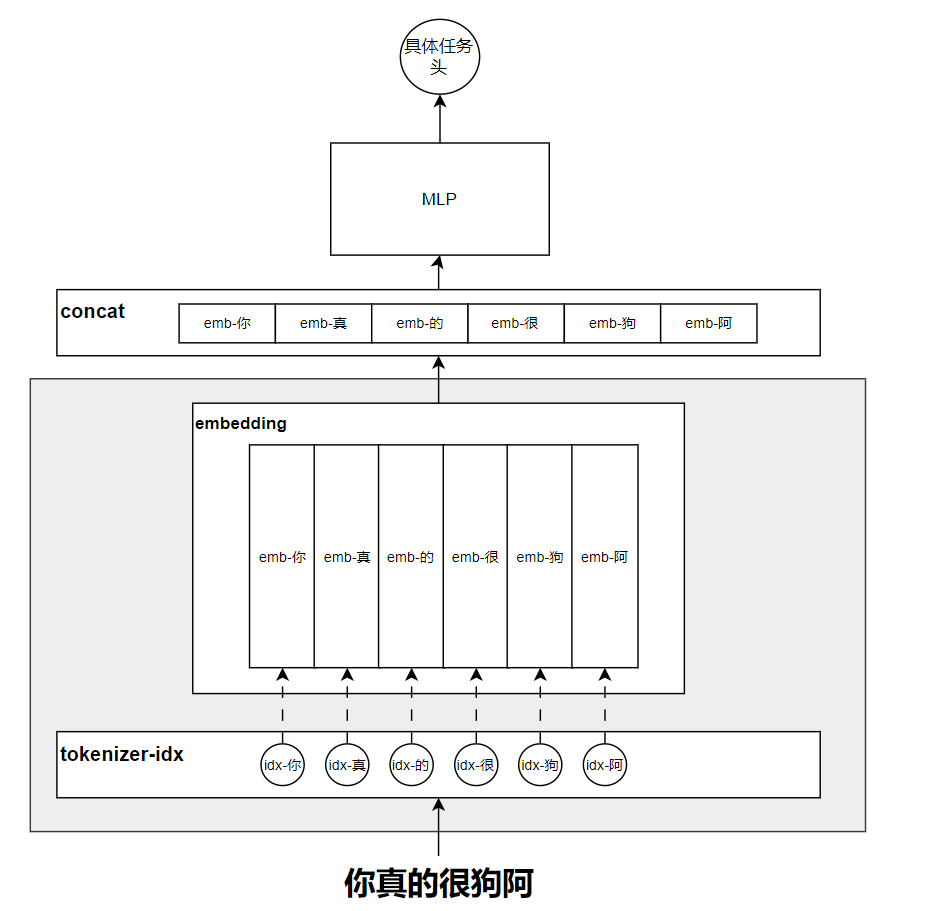
首先对于上面的网络，可以看作两大部分：

1. 阴影部分可以看作是对token的embedding学习和构建；
2. 阴影部分之上的可以认为是具体的网络设计。

对整个网络的运行步骤进行总结一下：

1. 将利用tokenrizer分词器将“你真的很狗阿”这句话切分为token级别，同时将切分后的每一个token映射到一个具体的id。
2. 构建一个可学习的embedding矩阵，这个矩阵大小取决于我们总的词库切分出来的总的token数，并不只是这句话仅有的这几个词切出来的token数。总之每一个token对应一个可学习的embedding向量。
3. 将“你真的很狗”这句话对应的embedding向量取出来，进行拼接，当然也可以是对应位置的加和，或者是其他操作，最常用的是横向拼接。
4. 将concat拼接后的向量送入到MLP网络进行学习。

缺点

首先我们还是强调一下，每一个对应的embedding向量就是表示具体token的信息，那上面的这种传统解决方案来说，每一个embedding是独立的。这就和我们最开始强调的“NLP任务特点”不契合了。所以在图中的阴影部分（用于学习token的embedding）就是我们首先要考虑改进的地方。

改进思路

在NLP任务特点的章节表明，每一个词都似有若无的和它前后的词（也称为上下文）是有联系的，那要完成好NLP任务，就不能像传统方法一样独立的考虑每一个词或者token的信息。而是要综合考虑上下文的信息，那如何考虑呢？最直觉的方法就是将上下文的信息叠加到当前token上，叠加方法中最简单的就是加和了。大致如下图所示：

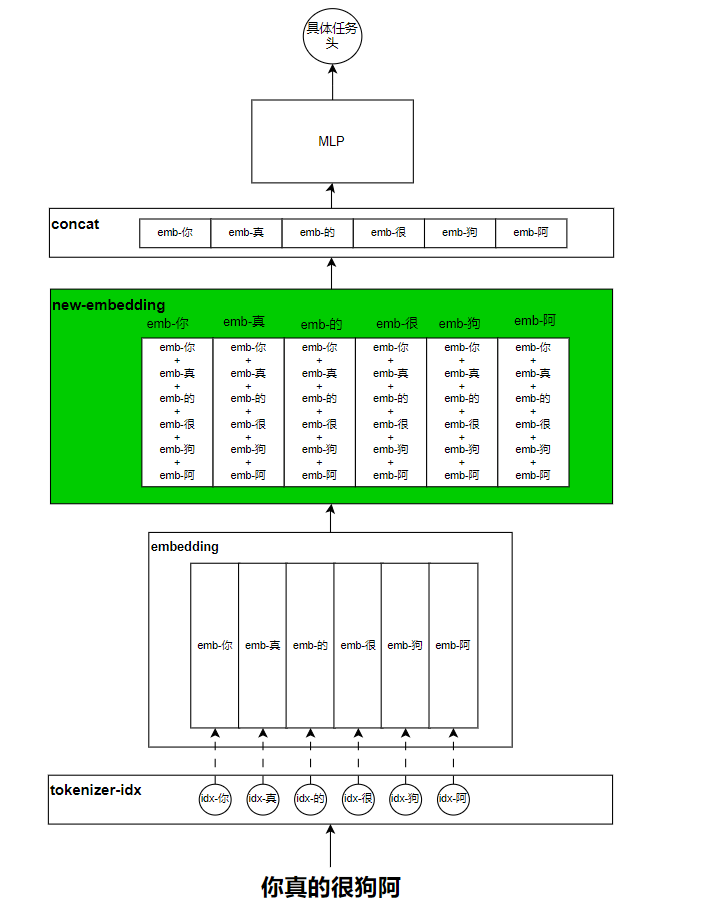
绿色的地方就是我们改进的地方，但是这就有一个非常大的问题，那就是融合上下文之后的每一个token的新embedding信息都一样了，这显然是不对的，因为不具有区分性了，那又该如何改呢？

首先我们分析一下，这种简单加和的本质是因为我们将上下文的token对当前token的影响程度都看成是一样的，且影响权重都是1。我简单给一个公式：

$newem{b}_{你}=w_0\ast em{b}_{你}+w_1\ast em{b}_{真}+w_2\ast em{b}_{的}+w_3\ast em{b}_{很}+w_4\ast em{b}_{狗}+w_5\ast em{b}_{阿}$
其他的词的的emb的计算类似。而简单加和的本质就是将所有的w参数都看作是1，这个w可以看作是上下文的每一个token对当前token的影响程度。但是，上下文的token对当前token的影响程度显然是不一样的

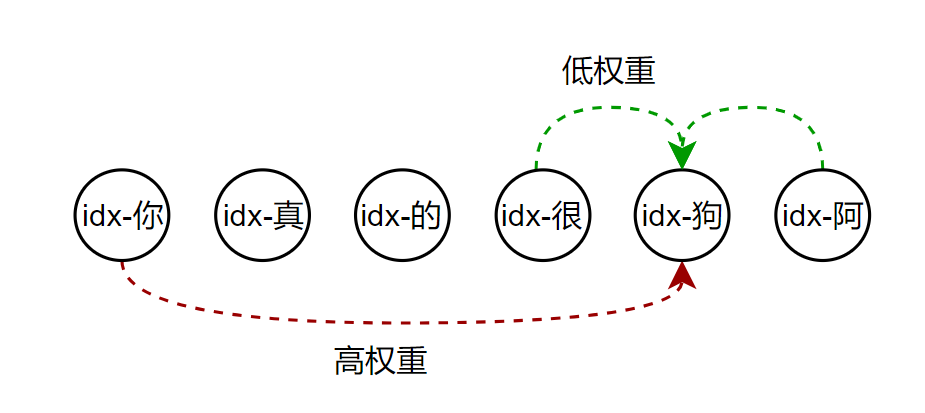
就拿这句话来说，如果要把握住“狗”这个词的具体含义，“你”这个词对他的影响程度是大于其他词对他的影响程度的。所以原始公式中的权重 $w$ 应该不能同等的看作是1，那具体是多少呢？按照以往神经网络的处理习惯上，这个 $w$ 的权重我们可以让模型自己去学习。到这里或许我们可以回想一下word2vec的原理，之前我写过的一篇：word2vec的原理和难点介绍(skip-gram,负采样、层次softmax)的博客中讲到，模型训练完之后得到了词的embedding矩阵，而词与词的embeding向量的点积计算的结果可以间接性的表示词与词之间的相似度。那放到我们现在的问题中，我们同样可以将token与token对应的embedding的向量点积看作是token与token之间的影响程度，同时这里embedding是不断学习的，那自然点积结果就是不断变化学习的，这也就实现了我们的愿望：动态学习$w$权重。我们可以稍微绘制一个图看一下：

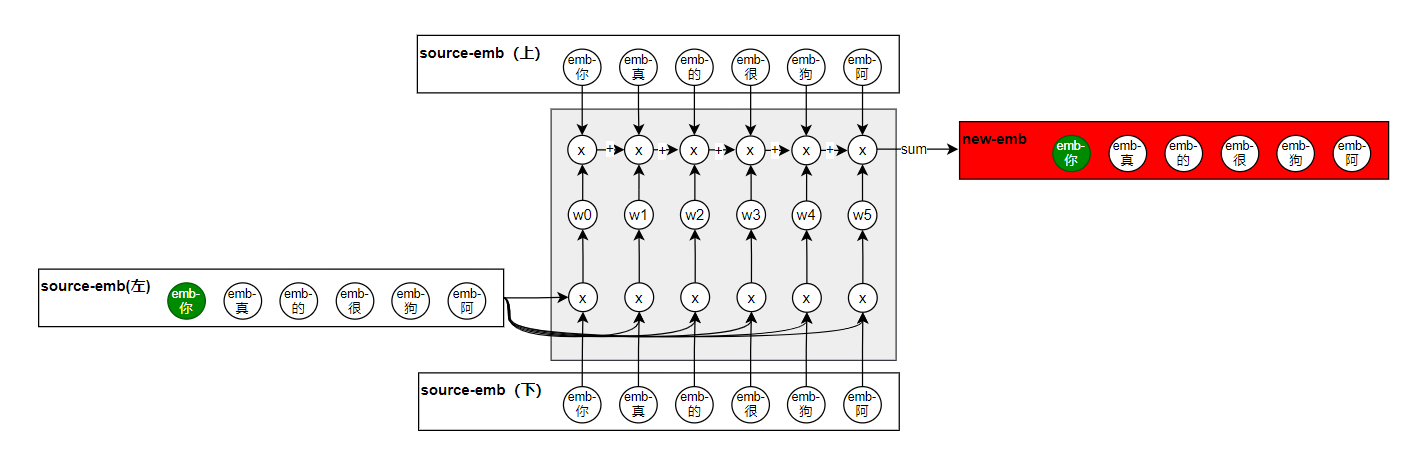
这里的三个emb的输入都是一样的，source-emb(左)和source-emb(下)用于计算出权重$w$，结合着我最初的给公式来看这个图，就很清晰了。其实到这里，看似是已经实现了我们的诉求了，但是你细看这个结构，你会发现并没有可训练的参数，当然你可能会说，输入的三个embding都是可以学习的参数，确实在这个场景下这三个emb是可学习，但是你想一下，如果你输入的特征本身就是数值型特征，那也就不会有emb了，这样整个网络就没有可学习的参数了，所以为了解决这个问题，分别在三个emb矩阵输入的地方都加入了linear层：

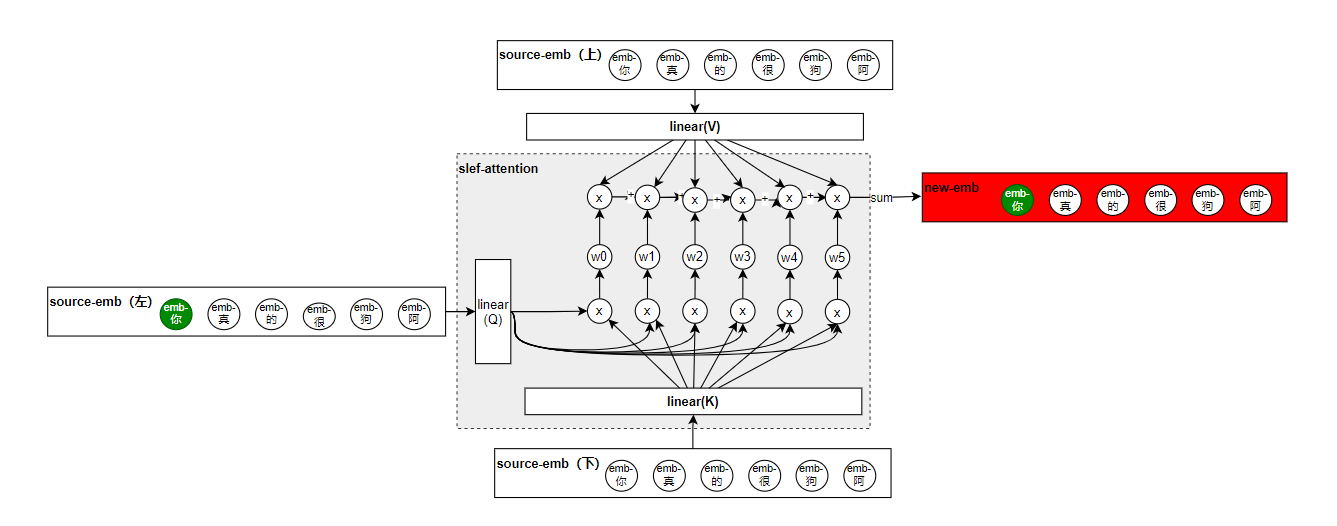
这样加入了三个linear层之后，就有可学习的参数了，这三个层我们分别叫它query(Q)，key(K)和value(V)。其中涂色的地方就是self-attention的雏形。为了看懂这个图，下面举例子讲解一下：

计算“你”的新embedding时：

1. 计算其他词对“你”的影响权重（向量点积）

	你（key）	真（key）	的（key）	很（key）	狗（key）	阿（key）
你（query）	w00	w01	w02	w03	w04	w05
真（query）

2. 将计算得到的权重与对应的token的value向量进行相乘，然后加和得到新的embedding向量

$$endem{b}_{你}=w00\ast em{b}_{你}+w01\ast em{b}_{真}+w02\ast em{b}_{的}+w03\ast em{b}_{很}+w04\ast em{b}_{狗}+w05\ast em{b}_{阿}$$

计算“真”的新embedding时：

1. 计算其他词对“真”的影响权重（向量点积）

	你（key）	真（key）	的（key）	很（key）	狗（key）	阿（key）
你（query）
真（query）	w10	w11	w12	w13	w14	w15

2. 将计算得到的权重与value向量进行相乘，然后加和得到新的embedding向量

$$endem{b}_{真}=w10\ast em{b}_{你}+w11\ast em{b}_{真}+w12\ast em{b}_{的}+w13\ast em{b}_{很}+w14\ast em{b}_{狗}+w15\ast em{b}_{阿}$$

以上就是self-attenion的大致原理，但是还是和原文给出的self-attenion的结构是不一样的：

对比一下发现，多了Scale、Mask、和SoftMax，首先Mask忽略掉，后边讲解码器的时候我会讲。

那么这个Attention的公式呢就可以归结为下面的这个了：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

SoftMax是很好理解的，做一个归一化的处理，问题就在于这个Scale，Scale的做法呢就是在QK点积后除以QKV（他们三个的维度是一样的）的维度的根号，为什么要除以这个维度，这就要说到注意力的种类，根据注意力的计算形式，会把注意力分为加性注意力和乘性注意力，而我们这里呢就属于乘性注意力，而因为当下的很多矩阵计算框架中，对乘积的计算速度优化更好，所以作者呢就选择了用乘性注意力，在使用过程中他们发现，如果qkv的维度较小的时候，这两种注意力的最终效果都是差不多的，但是当维度变大之后，乘性注意力效果就变差了。他们猜测是因为维度变大之后，乘积的结果也跟着变大，导致最后梯度计算的时候出现了问题，所以就除以一个维度的根号值，这就是Scale。最终的效果如下，大家可以和上面的原文中的图对比来看。

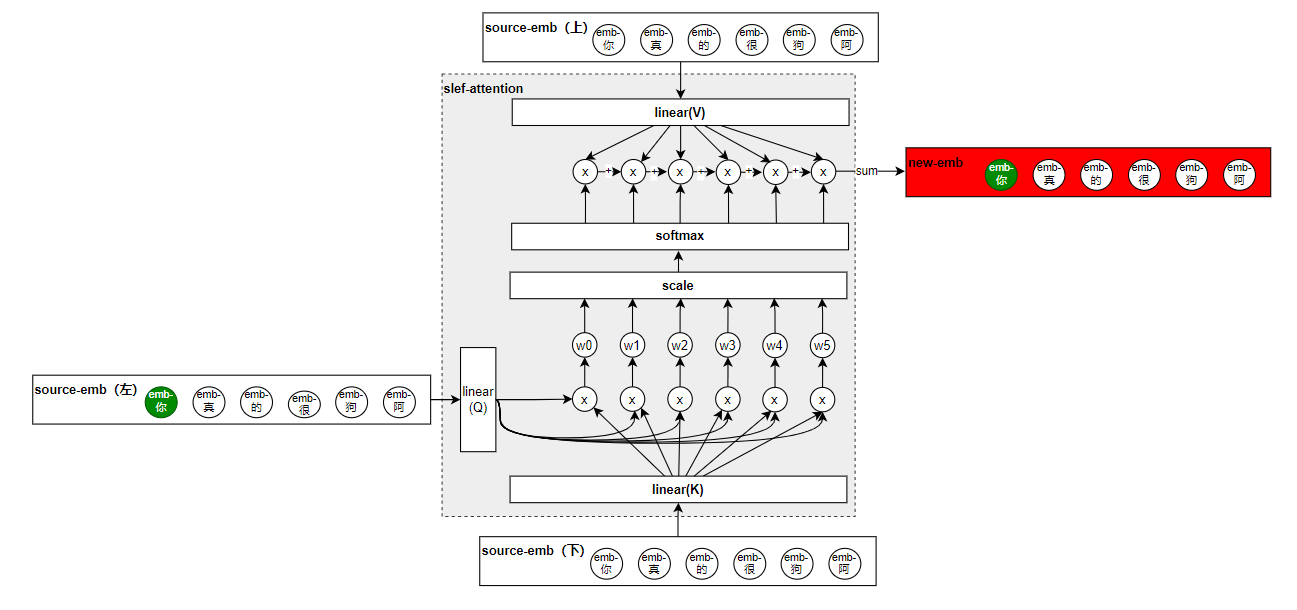
多头注意力（Multi-Head Attention）

上面已经讲明白了self-attention,而Multi-Head Attention就是横向的多个self-attention叠加，这么做的出发点是在于：希望模型从多个维度和层面去学习token的信息，比如说“你真的很狗阿”，这个“狗”字，我们希望从多个维度去把握，好比你可以理解为，有一个self-attention是纯从动物维度去学习这个token的信息的，而另一个self-attention则是从人类角度去学习的。这就是多头注意力的出发点。最后将每一个self-attention执行结果进行concat送入到一个linear层就ok了。

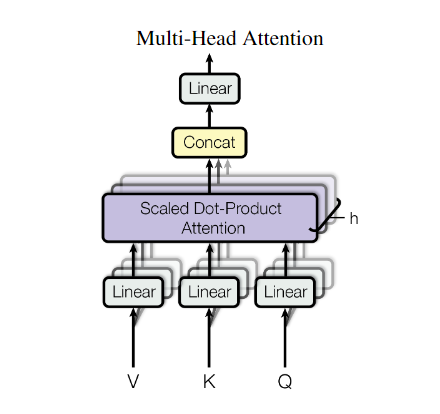
注：结合着上图来看，以及按照我讲解的原理来说，有多少个头，就代表着有多少套（QKV），也就是表示应该有多少套Linear层，但是实际的实现中，这样做参数会非常大，难以训练，我们只会创建一套QKV层，然后均分出几份作为不同的注意力头的QKV。

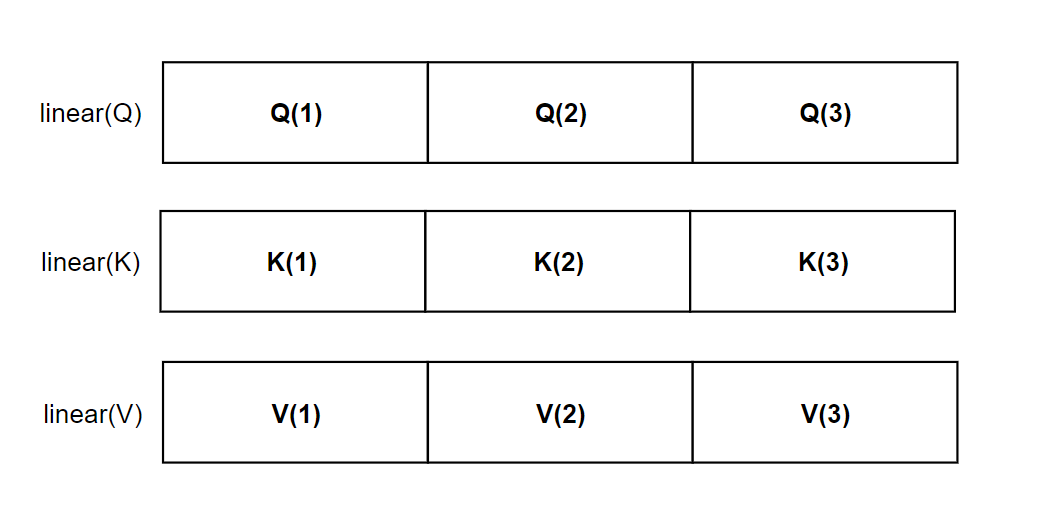
要实现均分，也就产生了一个严格的要求：

1. 也就是QKV的维度d_model要能够整除多头注意力的头数h

这一点要牢记，这是代码实现时候的细节点。在transformer这篇文字中，头数h=8。

Encoder部分

还是老样子，我们先不看论文中的结构，我们看看最开始那个网络：

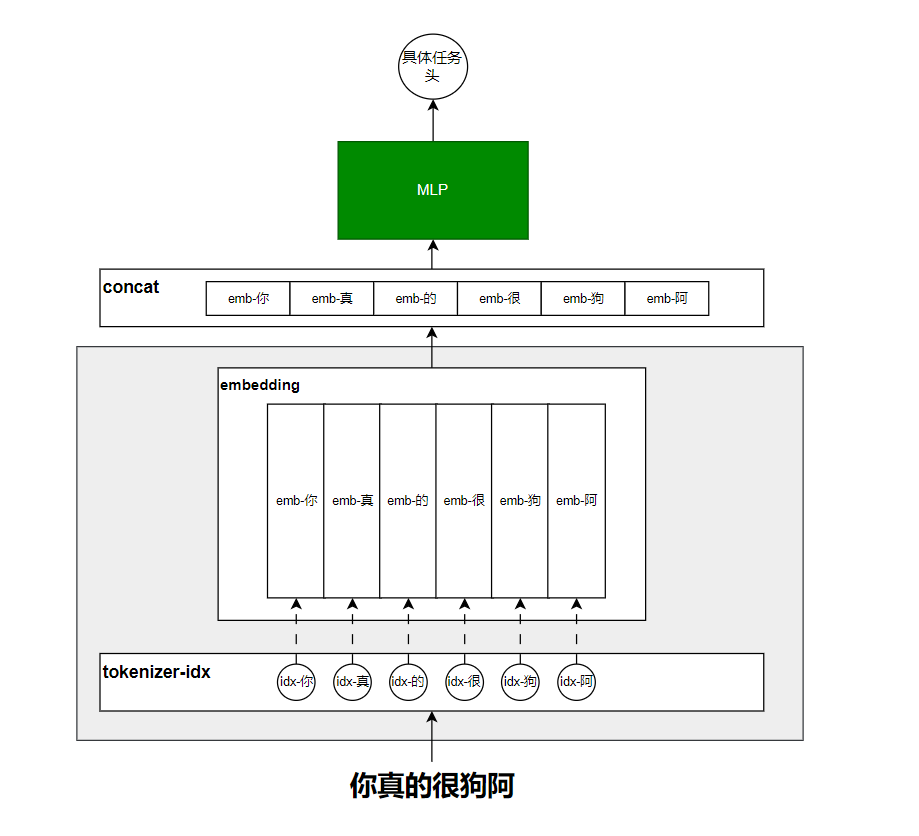
我们前面花了很大力气讲的self-attention和Multi-Head Attention其实就是在改造灰色阴影部分，这部分其实你可以认为只是在处理embedding问题，思考如何得到一个包含上下文的token的新的embedding而已，而蓝色的部分才是真正要送入的网络。这个网络就可以五花八门了，你可以是传统的MLP，也可以是CNN等，而transformer也就是用了一个传统的两层MLP而已：

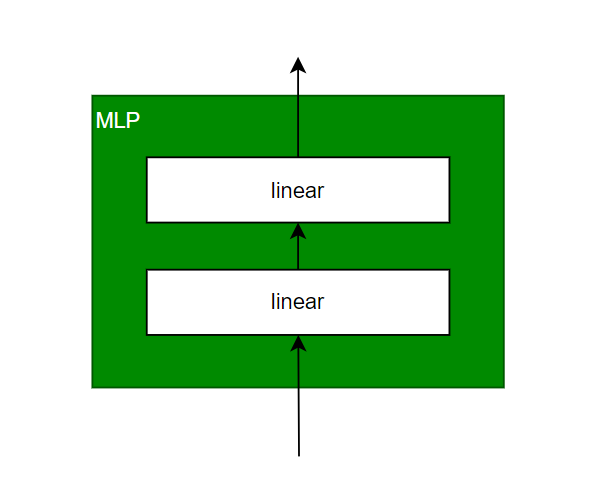
ok，transformer的整体结构就这么出来了，下面放一下原文中的结构图：

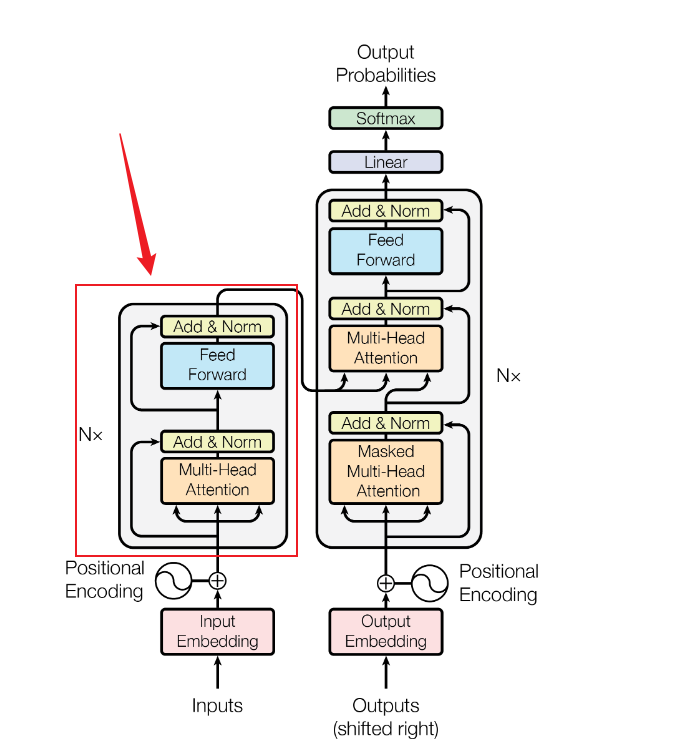
可以看得出来，我们已经把核心的骨干结构都讲出来了，而考虑到网络的收敛速度和平稳性，整体结构上利用了残差连接，同时呢多头注意力的输出和前馈神经网络的输出都用了一个LaryNorm进行了归一化处理。这就是图中的Add&Norm。

那就结束了，总结一下encoder部分的操作步骤：

1. 输入经过一个Multi-Head Attention得到新的融合了上下文的embedding，这个多头注意力整体利用残差网络结构连接。
2. 新的embedding经过LayerNorm进行归一化处理
3. 继续将LayerNorm结果送入到前馈神经网络（两层MLP），整体结构同样采用残差连接
4. MLP的结果送入到LayerNorm进行归一化处理。

大概的一个encoder的原子结构就是这样子了。transformer就是复制了6个这样的结构，作为encoder。

注：通过上面的分析，我觉得需要注意的点在于：

1. 整体结构是先残差计算，然后LayerNorm，这个别搞反了。
2. 整体分析下来，其实网络可调的超参并不多，在多头注意力部分，可调的就是QKV的维度，在前馈神经网络可调的就是隐藏层的维度（这里考虑的是不更改网络的任何结构，包括MLP的层数）。在transformer原始实现中，QKV的维度d_model被设置为了512，前馈神经网络的隐层维度d_ff被设置为了2048

Decoder部分

decoder的结构其实和encoder部分的结构是很类似的，只是在最底部多了一个Masked Multi-Head Attention。

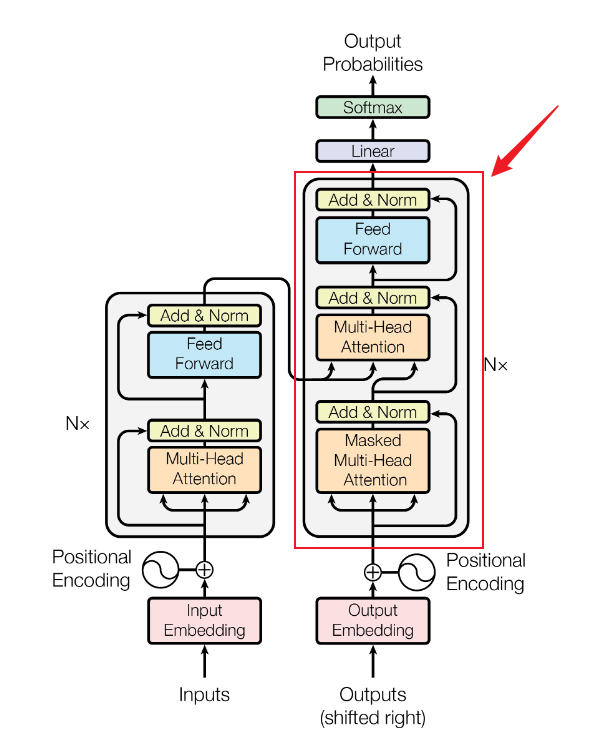
提出这篇文章的时候，作者们主要是在关注机器翻译问题，所以我们也就拿翻译来举个例子：

源语言	目标语言
你真的很狗阿	You’re such a jerk

对于这个任务，我们会将源语言丢到编码器学习，然后翻译出目标语言，而目标语言的翻译就是一个词语接龙的过程，翻译出的token会重新输入到解码器中，用于后面的token的生成。这也就表明，我们在训练transformer的时候，解码器部分，我们不希望让token看到未来的信息。比如在预测such的时候，我只希望它看到you are两个词，在预测a的时候，只希望看到you are such这几个词。对于未来的token，我们不需要加入这部分上下文的信息。那该如何做呢？首先我们self-attentionl的qk来计算出注意力分数：

	You（key）	are（key）	such（key）	a（key）	jerk（key）
You（query）	w00	w01	w02	w03	w04
are（query）	w10	w11	w12	w13	w14
such（query）	w20	w21	w22	w23	w24
a（query）	w30	w31	w32	w33	w34
jerk（query）	w40	w41	w42	w43	w44

接下来要根据公式和注意力分数计算出新的embedding了,为了说明例子，我直接从are举例：

$$newem{b}_{are}=w10\ast em{b}_{you}+w11\ast em{b}_{are}+w12\ast em{b}_{such}+w13\ast em{b}_a+w14\ast em{b}_{jerk}$$

在这个计算公式中，为了不融入未来token的信息（such、a、jerk）。我们的做法就是将对应的权重变为0，那如何变为0呢，这个就要了解softmax的公式了，因为这个qk计算得到的权重分数w最终是要经过softmax计算的。
$$Softmax(x)=\frac{e^{x_i}}{{\sum }_i^{}{e}^{x_i}}$$

你可以认为$x_i$是qk计算后再scale的分数，最后再经过softmax进行计算，为了让最终的softmax值为0，那输入的$x_i$就应该为负无穷，因为e的负无穷次方约等于0。所以我们只需要在前面qk点积计算的时候将未来的token的分数变为负无穷就ok了。

	You（key）	are（key）	such（key）	a（key）	jerk（key）
You（query）	-inf	-inf	-inf	-inf	-inf
are（query）	w10	-inf	-inf	-inf	-inf
such（query）	w20	w21	-inf	-inf	-inf
a（query）	w30	w31	w32	-inf	-inf
jerk（query）	w40	w41	w42	w43	-inf

上面就是我们要实现的效果，而为了实现这个效果，通常我们会建立一个同等维度的矩阵，叫Mask矩阵

0	0	0	0	0
1	0	0	0	0
1	1	0	0	0
1	1	1	0	0
1	1	1	1	0

到时候是根据qk计算生成一个分数矩阵，然后再建立一个同等维度的Mask矩阵，这个矩阵的上三角都是0，然后我们会根据Mask矩阵的0和1情况，在分数矩阵中将0对应的位置更改为负无穷，这就是Mask的由来。最后进行softmax的时候，这些位置的权重就会变为0了。ok关于decoder的核心就这么点了。

注：大体结构差不多都讲完了，同样decoder需要注意1点：

1. 第二个多头注意力的KV是来自encoder的输出的。Q是来自上一个Masked Multi-Head Attention的输出。
2. 整体的decoder也是6层。

数据输入

搞定了整体的模型结构，接下来我们就讲解一下输入了，而输入部分就是token的embedding编码和token的位置编码之和。

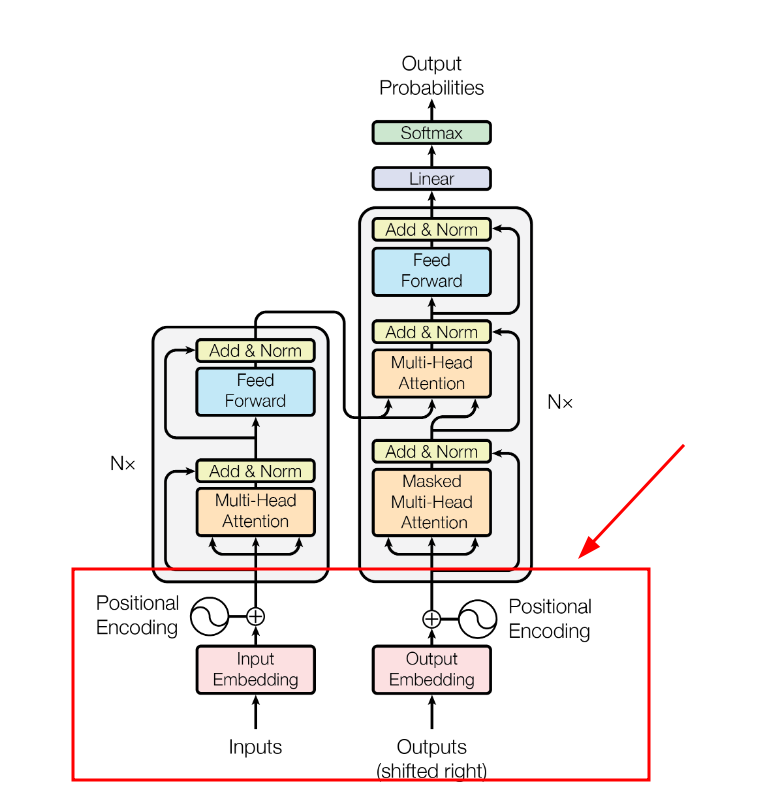
token的embedding编码

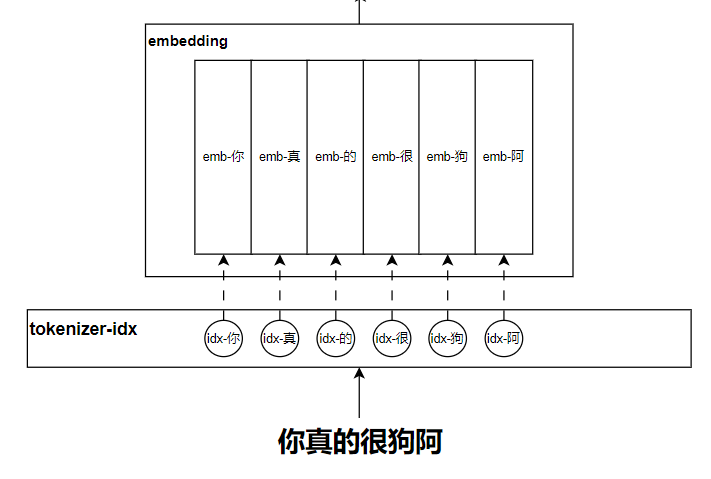
在讲解self-attention的时候，我们就已经提到了embedding作为输入了，这里简单讲讲这个embedding吧。
我们在做NLP任务的时候，最原始的信息肯定就是文本，但是输入到模型计算的时候一定得是一组数字或者是一组向量，所以通常会利用tokenizer分词器把长文本切分为多个token，并把每个token映射到一个对应的id，然后每一个id再映射到一组向量上。而这组向量就作为这个token的表示，它是可学习的。这就是embedding。结合下图来理解理解吧：

绝对位置编码

原理

前面讲到了self-attention的特点就在于可以并行的加载token，这样会带来一个不好的地方在于它无法区分每一个token的位置了，就好比把所有的token都放到一个篮子里，根本没有顺序可言，但是文本的位置信息是很重要的，就好比你在做词性分析的时候，动词后面大概率名词。所以位置信息不能丢。在transformer论文中，利用了正余弦函数来表示位置编码，具体公式如下：

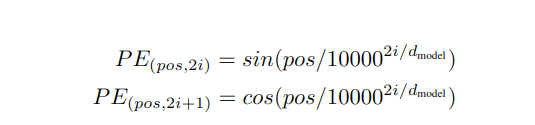
对变量进行必要的说明：

1. pos：token在句子中的位置
2. i：向量中的每一个值的位置
3. d_model：向量维度

因为token的位置编码是要和token的embedding编码相加的，所以位置编码的整体维度要和token的embedding的维度一样，这就是d_model：

而这个向量中的i则表示具体的空格的数字了，偶数位（2i）的计算则就利用第一个公式，奇数位（2i+1）的计算则利用第二个公式。

ok，这样位置编码向量就被计算出来了，而这种计算方法我们也称之为绝对位置编码，最终的模型输入就是一整句话的token向量，而每一个token的向量表示都是token的embedding编码和对应位置编码的和。

绝对位置编码优点

最后我想强调一下就是，在绝对位置编码上主要是为了引入位置信息，也就是公式中的pos，按理来说用什么公式都可以，只要有关于pos的计算就可以，但是为什么整体要用sin和cos呢？

因为sin和cos是可以互相转换的，那么我就讲讲sin。首先我们来看一个关于sin四则运算的公式:

$$sin(pos+k)=sin(pos)cos(k)+cos(pos)sin(k)$$

这里的$pos+k$表示的是一个位置，$pos$也是一个位置，那$k$就是他们之间的相对位置距离。通过展开来看，我们是可以计算得到cos（k）和sin（k）的值，也就是说利用sin的这种方式，是可以学习到一些相对位置的信息的，而相对位置的学习一定程度上决定了模型的外推能力。这就是选择sin的原因。同时还有一个好处在于，这些位置编码是一次性计算出来的，根本不需要学习，这就给模型学习减少了很多的压力。

同时呢，transformer作者们也试过像token的embedding编码这样将位置也进行embedding编码，让他们变得可学习，但是他们发现最终效果和sin这种差不多。既然效果差不多，而embedding的形式要引入很多学习的压力，所以他们选择了第一种。但是OpenAI在GPT1和GPT2中，他们却用了这种可学习的embedding形式，这就是我想不明白的地方。

模型训练

训练数据集

在原论文中，选择了WMT2014的英德数据和英法数据，主要是做翻译任务。

硬件

原文用了8卡P100的GPU机器

训练参数

1. 优化器采用Adam，其中参数β1 = 0.9,，β2 = 0.98 ， ε = 10−9.
2. 学习率动态变化，具体公式如下，step_num是训练步数，warmup_steps=4000：
   

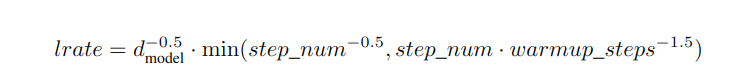
总结

最后我们对这篇文章进行一下总结

1. transformer整体采用encoder-decoder结构
2. encoder结构采用Multi-Head Attention+两层前馈神经网络结构，两个结构整体上采用残差连接形式。总共有6个这样的块组成encoder
3. decoder结构采用Masked Multi-Head Attention+Multi-Head Attention++两层前馈神经网络结构，三个结构整体上采用残差连接形式。总共有6个这样的块组成decoder
4. d_ff维度为2048，d_model=512，h=8
5. 输入采用embedding编码+绝对位置编码
6. 优化器采用Adam，其中参数β1 = 0.9,，β2 = 0.98 ， ε = 10−9.
7. 学习率动态可调

从整体的结构来看，self-attention的结构并不需要多深，就可以实现对上下文信息的深度融合，这也就表明它可以比RNN训练得快，同时它可以并行的加载数据，而RNN是不可以的，这样速度更快。等于说transformer就是解决了RNN系列的一些弊端，也就从此刻开始，transformer取代RNN系列，占据NLP的铁王座地位。

transformer的缺点

以上把所有的transformer知识都讲解了一下，但是凡事总会有优缺点，而transformer最大的缺点就在于它的位置编码，它采用绝对位置编码的形式来引入位置信息，以假设的形式猜测sin这种模式可以引入相对位置信息。但是整体的外推能力并不强，这就是早期的大模型为啥生成的最长文本都很短，后来的大佬们发力点就在位置编码上，诸如现在的RoPE，连transformer作者们也意识到这一点，所以他们在后一年（2018-07）也改进了位置编码，接下来我就会读一下这篇文章，尽情期待。

ok，整体分析就到这，也推荐大家阅读阅读原文：Attention Is All You Need