516. 最长回文子序列
给你一个字符串
s,找出其中最长的回文子序列,并返回该序列的长度。子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab" 输出:4 解释:一个可能的最长回文子序列为 "bbbb" 。
示例 2:
输入:s = "cbbd" 输出:2 解释:一个可能的最长回文子序列为 "bb" 。
提示:
1 <= s.length <= 1000
s仅由小写英文字母组成
1.
回文串子序列.
[i,j]区间最长回文子序列,如果s[i]==s[j],dp[i][j]=dp[i+1][j-1].
如果s[i]!=s[j],dp[i][j]=max(dp[i+1][j],dp[i][j-1]).
2.
利用记忆化递归填表,可以很快处理边界,不需要考虑填表顺序.
边界情况,i==j时,renturn 1.
i>j时,return 0.
class Solution {
public:
string s; // 储存输入字符串
int n; // 字符串长度
vector<vector<int>> dp; // 动态规划数组,dp[i][j]表示从第i到第j个字符之间的最长回文子序列长度
void solveinit() {
n = s.size(); // 获取字符串长度
dp.clear(); // 清空动态规划数组
dp.resize(n, vector<int>(n, -1)); // 初始化动态规划数组,全部置为-1
}
int dfs(int i, int j) { // 递归函数,用于计算从第i到第j个字符之间的最长回文子序列长度
if (i > j) { // 如果i大于j,说明越界了,返回0
dp[i][j] = 0; // 将dp[i][j]置为0
return dp[i][j]; // 返回0
}
if (i == j) { // 如果i等于j,说明只有一个字符,是回文子序列,返回1
dp[i][j] = 1; // 将dp[i][j]置为1
return dp[i][j]; // 返回1
}
if (dp[i][j] != -1) // 如果dp[i][j]不为-1,说明已经计算过,直接返回结果
return dp[i][j]; // 返回dp[i][j]
if (s[i] == s[j]) { // 如果第i个字符和第j个字符相同
dp[i][j] = dfs(i + 1, j - 1) + 2; // 则最长回文子序列长度等于去掉两端字符后的子序列长度加2
} else { // 如果第i个字符和第j个字符不相同
dp[i][j] = max(dfs(i, j - 1), dfs(i + 1, j)); // 则最长回文子序列长度等于去掉第i个字符后的子序列长度和去掉第j个字符后的子序列长度的最大值
}
return dp[i][j]; // 返回dp[i][j]
}
int longestPalindromeSubseq(string _s) { // 主函数,求最长回文子序列的长度
s = _s; // 将输入字符串赋值给成员变量s
solveinit(); // 初始化
for (int i = 0; i < n; i++) { // 遍历字符串的所有子序列
for (int j = i; j < n; j++) {
dfs(i, j); // 计算从第i到第j个字符之间的最长回文子序列长度
}
}
return dp[0][n - 1]; // 返回整个字符串的最长回文子序列长度
}
};
二叉树
描述
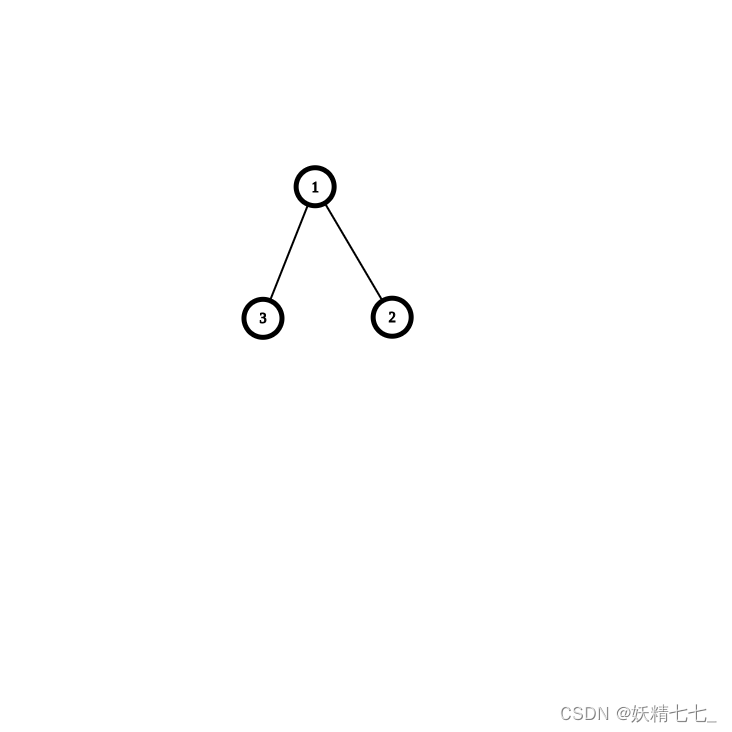
小强现在有nn个节点,他想请你帮他计算出有多少种不同的二叉树满足节点个数为nn且树的高度不超过mm的方案.因为答案很大,所以答案需要模上1e9+7后输出. 树的高度: 定义为所有叶子到根路径上节点个数的最大值.
例如: 当n=3,m=3时,有如下5种方案:
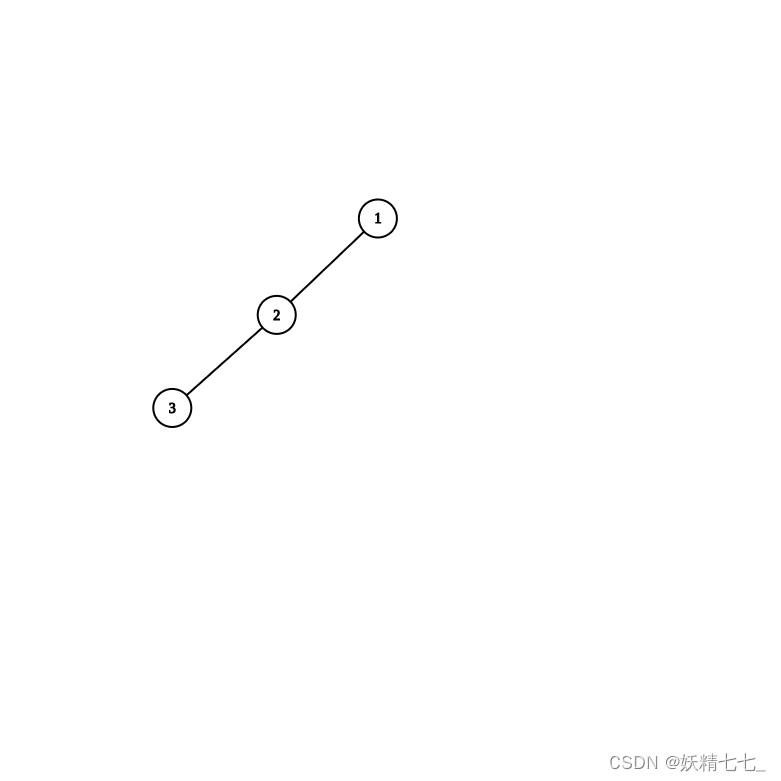

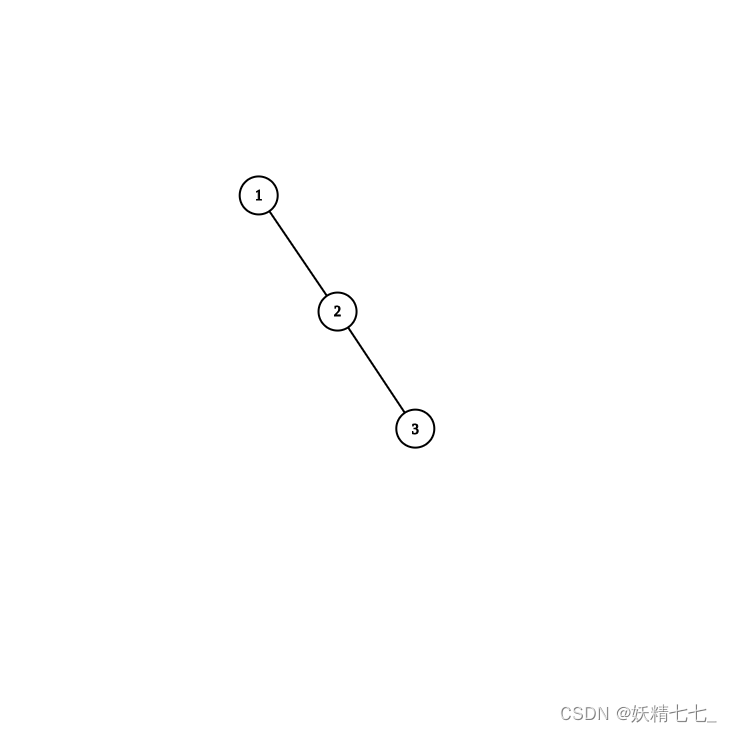

数据范围:1\le n,m\le 50\1≤n,m≤50
进阶:时间复杂度O(mn^2)\O(mn2) ,空间复杂度O(nm)\O(nm)
输入描述:
第一行输入两个正整数nn和mm. 1\leq m \leq n \leq 501≤m≤n≤50
输出描述:
输出一个答案表示方案数.
示例1
输入:
3 3
复制
输出:
5
复制
示例2
输入:
3 2
复制
输出:
1
复制
示例3
输入:
4 3
复制
输出:
6
复制
1.
集合,拿一个元素当作是头节点,还剩下n-1个节点,枚举左边节点数量,分布乘法.
#if 1
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using p = pair<ll, ll>;
int dx[] = { 1, -1, 0, 0 }; // 定义上下左右四个方向的增量数组
int dy[] = { 0, 0, 1, -1 }; //
const int MOD = 1e9 + 7; // 取模值
// 输入参数变量
int n, m;
// 存储输入变量
// 自定义变量
vector<vector<ll>> dp; // 动态规划数组,dp[i][j]表示节点数为i,高度不超过j的方案数
// 输入参数+存储输入变量
void init() {
}
// 初始化自定义变量
void solveinit() {
dp.clear(); // 清空动态规划数组
dp.resize(n + 1, vector<ll>(m + 1, -1)); // 初始化动态规划数组,全部置为-1
}
// 计算方案数的递归函数
ll dfs(int n, int m) {
if (n == 0) { // 如果节点数为0,返回1
dp[n][m] = 1;
return dp[n][m];
}
if (m == 0) { // 如果高度为0,返回0
dp[n][m] = 0;
return dp[n][m];
}
if (dp[n][m] != -1) return dp[n][m]; // 如果已经计算过,直接返回结果
ll ans = 0;
for (int i = 0; i < n; i++) { // 遍历左子树节点数
ans = (ans + (dfs(i, m - 1) * dfs(n - 1 - i, m - 1) % MOD)) % MOD; // 计算方案数并取模
}
dp[n][m] = ans % MOD; // 缓存结果
return dp[n][m];
}
// 解决问题
void solve() {
solveinit(); // 初始化
cout << dfs(n, m) << endl; // 输出方案数
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
while (cin >> n >> m) { // 循环读入数据
init(); // 输入参数处理
solve(); // 解决问题
}
}
#endif // 1
329. 矩阵中的最长递增路径
给定一个
m x n整数矩阵matrix,找出其中 最长递增路径 的长度。对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:
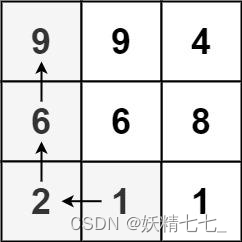
输入:matrix = [[9,9,4],[6,6,8],[2,1,1]] 输出:4 解释:最长递增路径为 [1, 2, 6, 9]。示例 2:
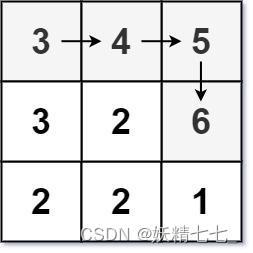
输入:matrix = [[3,4,5],[3,2,6],[2,2,1]] 输出:4 解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。示例 3:
输入:matrix = [[1]] 输出:1
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 2(31)1
暴力dfs搜索
1.
暴力递归搜索,超时.
class Solution {
public:
vector<vector<int>> mat; // 存储输入矩阵
int ret; // 最长递增路径的长度
int path; // 当前路径长度
int dx[4]={1,-1,0,0}; // 定义四个方向的增量数组
int dy[4]={0,0,1,-1}; //
int n,m; // 矩阵的行数和列数
// 初始化函数
void solveinit() {
ret=0; // 初始化最长递增路径长度为0
n=mat.size(); // 获取矩阵的行数
m=mat[0].size(); // 获取矩阵的列数
}
// 深度优先搜索函数,用于寻找最长递增路径
void dfs(int i,int j){
path++; // 当前路径长度加1
ret=max(ret,path); // 更新最长递增路径长度
for(int k=0; k < 4; k++){ // 遍历四个方向
int x=i+dx[k]; // 计算下一个位置的行坐标
int y=j+dy[k]; // 计算下一个位置的列坐标
if(x>=0 && x<n && y>=0 && y<m && mat[x][y]>mat[i][j]){ // 如果下一个位置合法且值大于当前位置
dfs(x,y); // 继续搜索
}
}
path--; // 回溯,当前路径长度减1
}
// 主函数,找出最长递增路径的长度
int longestIncreasingPath(vector<vector<int>>& _matrix) {
mat = _matrix; // 将输入矩阵赋值给成员变量mat
solveinit(); // 初始化
for(int i=0;i<n;i++){ // 遍历矩阵中的每一个位置
for(int j=0;j<m;j++){
path=0; // 初始化路径长度为0
dfs(i,j); // 从当前位置开始深度优先搜索
}
}
return ret; // 返回最长递增路径的长度
}
};
记忆化递归填dp表
class Solution {
public:
vector<vector<int>> mat; // 存储输入矩阵
int ret; // 最长递增路径的长度
int path; // 当前路径长度
int dx[4] = {1, -1, 0, 0}; // 定义四个方向的增量数组
int dy[4] = {0, 0, 1, -1}; //
int n, m; // 矩阵的行数和列数
vector<vector<int>> dp; // 动态规划数组,dp[i][j]表示从位置(i,j)出发的最长递增路径长度
// 初始化函数
void solveinit() {
ret = 0; // 初始化最长递增路径长度为0
n = mat.size(); // 获取矩阵的行数
m = mat[0].size(); // 获取矩阵的列数
dp.clear(); // 清空动态规划数组
dp.resize(n,vector<int>(m,-1)); // 初始化动态规划数组,全部置为-1
}
// 深度优先搜索函数,用于寻找最长递增路径
int dfs(int i, int j) {
if(dp[i][j]!=-1) return dp[i][j]; // 如果已经计算过,直接返回结果
int ans=0; // 初始化当前位置的最长递增路径长度为0
for(int k=0; k < 4; k++){ // 遍历四个方向
int x=i+dx[k]; // 计算下一个位置的行坐标
int y=j+dy[k]; // 计算下一个位置的列坐标
if(x>=0 && x<n && y>=0 && y<m && mat[x][y]>mat[i][j]){ // 如果下一个位置合法且值大于当前位置
ans=max(ans,dfs(x,y)); // 更新最长递增路径长度
}
}
}
dp[i][j]=ans+1; // 缓存结果
return dp[i][j]; // 返回当前位置的最长递增路径长度
}
// 主函数,找出最长递增路径的长度
int longestIncreasingPath(vector<vector<int>>& _matrix) {
mat = _matrix; // 将输入矩阵赋值给成员变量mat
solveinit(); // 初始化
for (int i = 0; i < n; i++) { // 遍历矩阵中的每一个位置
for (int j = 0; j < m; j++) {
ret=max(ret,dfs(i, j)); // 计算从当前位置出发的最长递增路径长度
}
}
return ret; // 返回最长递增路径的长度
}
};
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!





![[python数据处理系列] 深入理解与实践基于聚类的过采样与欠采样技术:以K-Means为例](https://img-blog.csdnimg.cn/direct/521c0646370b4df4a2794cebf37068cc.png)