目录

力扣334. 递增的三元子序列

解析代码

---

力扣334. 递增的三元子序列

334. 递增的三元子序列

难度 中等

给你一个整数数组 nums ，判断这个数组中是否存在长度为 3 的递增子序列。

如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ，使得 nums[i] < nums[j] < nums[k] ，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,4,5]
输出：true
解释：任何 i < j < k 的三元组都满足题意

示例 2：

输入：nums = [5,4,3,2,1]
输出：false
解释：不存在满足题意的三元组

示例 3：

输入：nums = [2,1,5,0,4,6]
输出：true
解释：三元组 (3, 4, 5) 满足题意，因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6

提示：

• 1 <= nums.length <= 5 * 10^5
• -2^31 <= nums[i] <= 2^31 - 1

进阶：你能实现时间复杂度为 O(n) ，空间复杂度为 O(1) 的解决方案吗？

class Solution {
public:
    bool increasingTriplet(vector<int>& nums) {

    }
};

---

解析代码

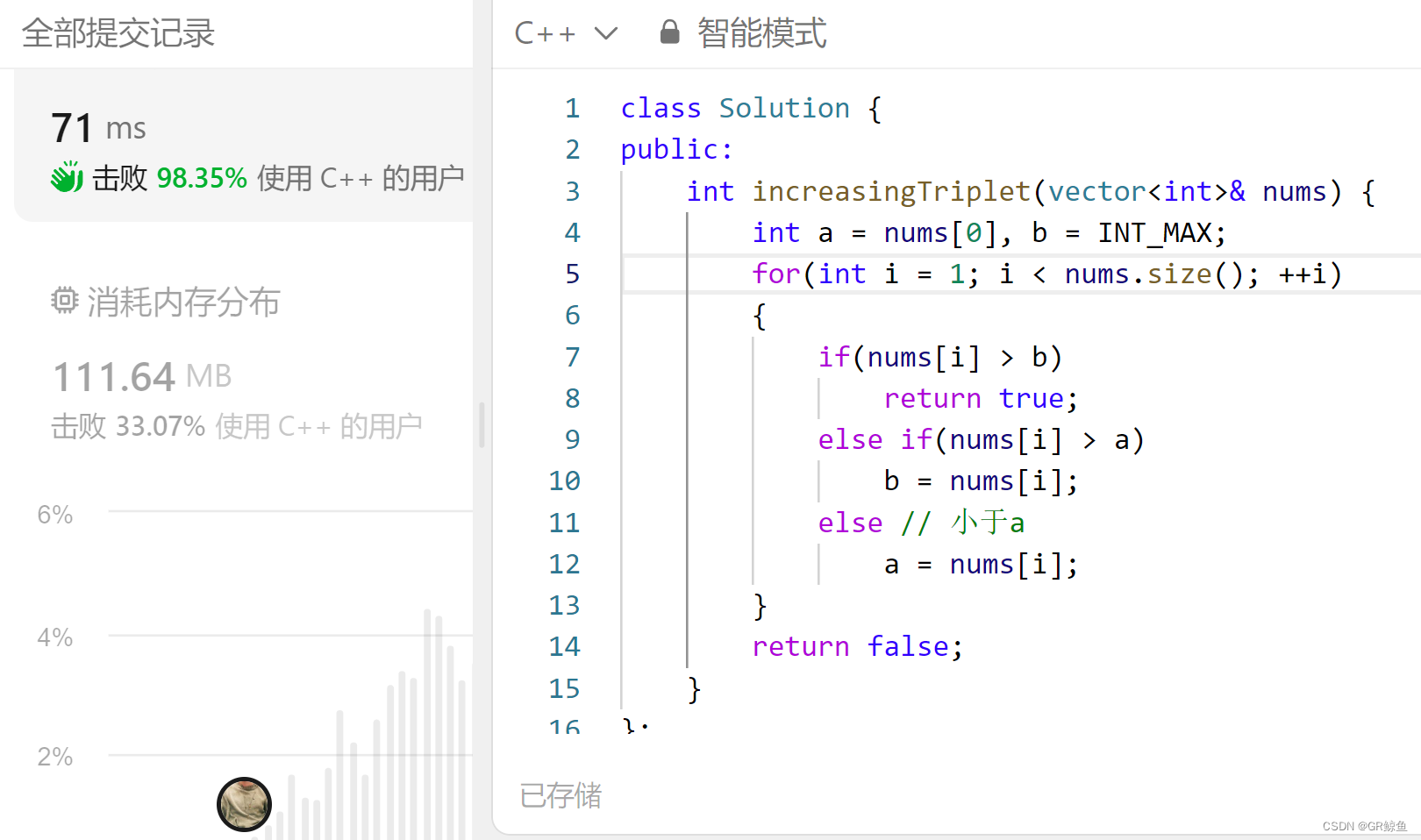
        贪心策略： 力扣300. 最长递增子序列的简化版。 不用一个数组存数据，仅需两个变量即可。也不用二分插入位置，仅需两次比较就可以找到插如位置。

class Solution {
public:
    int increasingTriplet(vector<int>& nums) {
        int a = nums[0], b = INT_MAX;
        for(int i = 1; i < nums.size(); ++i)
        {
            if(nums[i] > b)
                return true;
            else if(nums[i] > a)
                b = nums[i];
            else // 小于a
                a = nums[i];
        }
        return false;
    }
};