本文内容来源是B站——忠厚老实的老王,侵删。
三个坐标系和一些有关的物理量

使用 frenet坐标系可以实现将车辆纵向控制和横向控制解耦,将其分开控制。使用右手系来进行学习。

一些有关物理量的基本概念:


运动学方程
建立微分方程
主要是弄清前轮转角δf如何影响侧向位移和航向角?

运动学模型是不考虑轮胎变形,适用于轮胎变形较小的情况下,比如说低速时;动力学模型是考虑轮胎变形的因素。
运动学方程的建立如下:

上面的式子只体现了质心速度v对φ、X、Y的影响,没有体现前轮转角对X、Y、φ的影响,需要进一步的推导,最后一个式子是一个理论力学的知识,也就是一个刚体的角速度等于该刚体的线速度比线速度到速度瞬心的距离。严格来说V/R应该是航向角速度,也就是φ点+β点=V/R,但是运动学方程中默人β点是0,所以运行学方程假设过多,它也只适合低速情况下,高速情况不适用。
由正弦定理可得:

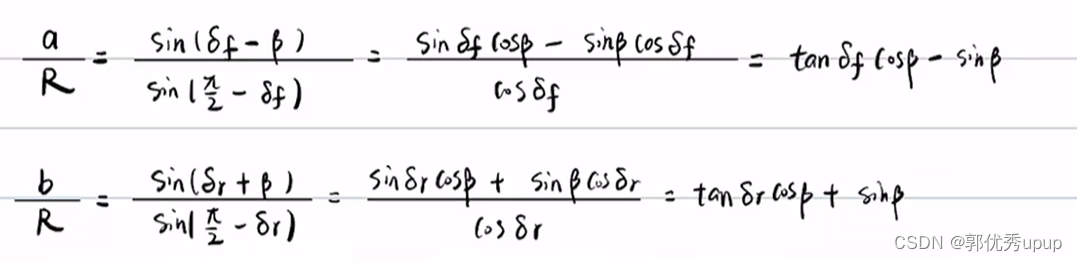
由于质心的位置是变化的,所以a和b的值也是不固定的,使用轴距L来表示R与δf和δr的关系。
经过 化简之后方程如下:
化简之后方程如下:
最终有:

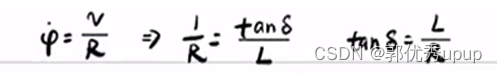
运动学方程只有在使用tanδ =L/R时需要或者坐标变换时需要,一般用不到,因为其简化过多。适合低速时,因为低速时轮胎变形不大,但高速时必须要考虑轮胎变形的影响。

由上图也可以看出在运动学方程中,纵横向控制是耦合在一起的,不能解耦控制。
动力学方程
frenet坐标系
特点:考虑了轮胎的动力学特性;选取frenet坐标系时,可以将纵向控制和横向控制进行解耦。
首先frenet坐标系方程如下:

上式子中使用了tanδ =L/R, 这个是由运动学方程推导而来,但在这里也依然适用,因为一般和横摆角相比,质心侧偏角都很小,因为质心侧偏角很大时车辆处于一种很危险的工况,不太可能会发生。
最后可以看出在frenet中纵向控制是可以解耦的(因为aτ只和速度v有关),而横向控制时是不能解耦的(因为an与v有关)。但当纵向控制稳定后,v几乎是不变的,此时an也只与δ有关。
此时的目标变成:将动力学方程和frenet坐标结合在一起就可以实现纵横向解耦控制。

上式子将纵向位移设置成是s,横向位移设置成d,aτ和s一个简单的二阶导数关系,也即使纵向控制相对简单,但是横向控制和方向盘转角不是简单的导数关系。![]() 的关系在汽车理论中详细的解释,但是是在车辆坐标下建立起来的,所以接下来的任务第一步:在车辆坐标系下建立车辆动力学模型得到
的关系在汽车理论中详细的解释,但是是在车辆坐标下建立起来的,所以接下来的任务第一步:在车辆坐标系下建立车辆动力学模型得到![]() ,第二步:再建立y和d的关系实现坐标变换到frenet坐标系中。第三部:最终得到
,第二步:再建立y和d的关系实现坐标变换到frenet坐标系中。第三部:最终得到![]() 的关系。
的关系。
第一步:二自由度车辆动力学模型
二自由度车辆动力学模型假设前轮转角δ较小,假设vx是一个常数,也就是它不管纵向控制,只管横向控制。
推导图文如下:





如下可以得到状态空间方程:其中符号和书中略有不用,请类比:(其中使用了β≈vy/vx)这里将前轮转角作为输入,车身速度和横摆角速度作为状态空间。
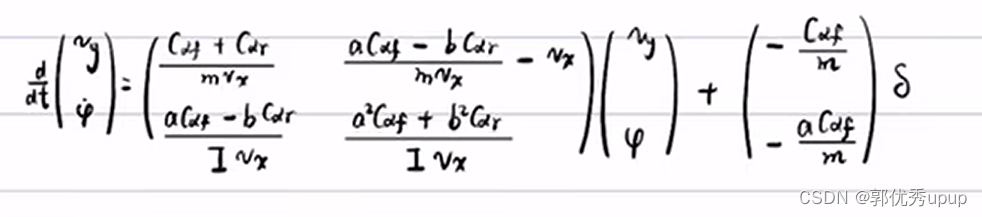


至此得到车辆二自由度运动学微分方程,以及其状态空间的表达形式。 可以反映出前轮转角怎样影响侧向速度和横摆角。
第二步:坐标变化

这里的u是前轮转角,在某一时刻规划得Xr以及![]() 都是已知的,并且
都是已知的,并且![]() 动力学方程也是已知的,最终会得到一个关于误差的微分方程,控制目标就是选择一个合适的u使得X和Xr尽量接近。
动力学方程也是已知的,最终会得到一个关于误差的微分方程,控制目标就是选择一个合适的u使得X和Xr尽量接近。
选择合适的代价函数使得误差最小:
例如一下三种选择:
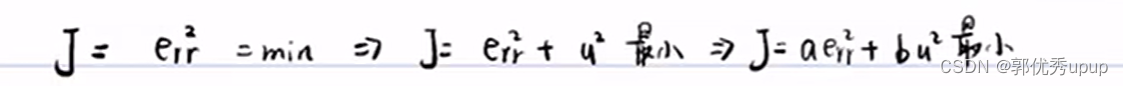
第一个是简单的使得误差最小,第二个是是的误差最小的同时也使得输入代价u最小;第三个是对误差和输入的各个分量配以权重。可将第三个代价函数(LQR)简化写成以下形式:

![]() 详细转换过程解析,需要注意的是
详细转换过程解析,需要注意的是![]() 是在自然坐标系上的:
是在自然坐标系上的:
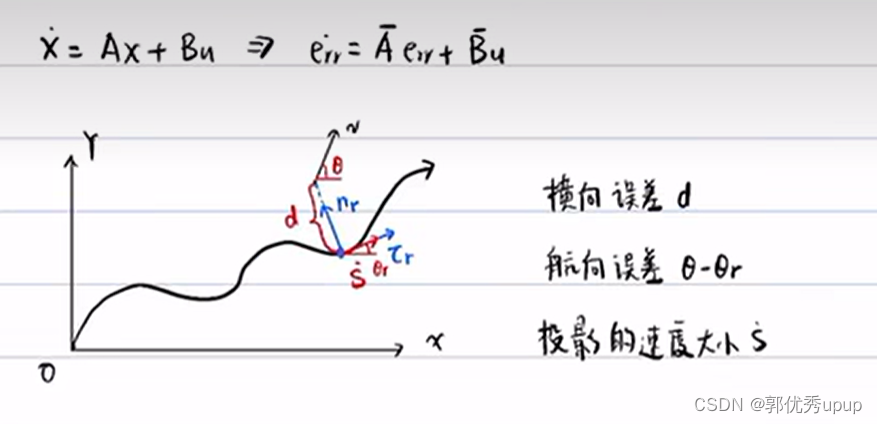
注:v是车身质心的速度,投影速度大小是S点,实际速度大小是v,这是代表速度大小,不代表速度方向,方向是横向控制的问题,方向由航向误差直接决定。这里的学习只考虑横向控制(也就是只考虑航向误差)。
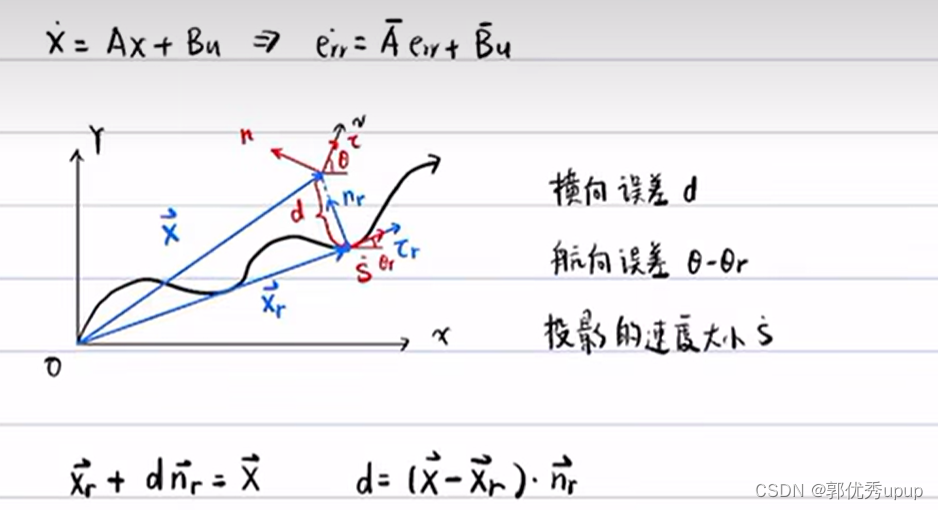
注:v是质心速度,θ是质心速度与绝对坐标系X轴的夹角也就是航向角,车身坐标系x轴是沿着车辆横摆角方向,τ是沿着质心速度v的方向。τ和车辆坐标系x轴差了一个质心侧偏角。蓝线X是车辆的实际位置和O的距离(车辆的真实位矢),Xr是参考点和O的距离(投影位矢)。
其中d是一个标量,不是一个向量,它和状态空间中的变量车身的侧向速度和横摆角速度没有直接关系。此时想将d与状态空间方程联系起来,对d进行求导运算。求导时需要注意nr不是一个常向量,它的大小是1,但是方向是随着轨迹的变化而变化。
向量位移分量的基本概念:
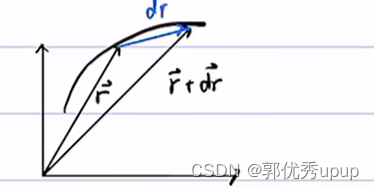
上图初始位矢是r,经过dt的时间它的位矢是r+dr,根据向量的三角形法则,dr就是蓝色的线。
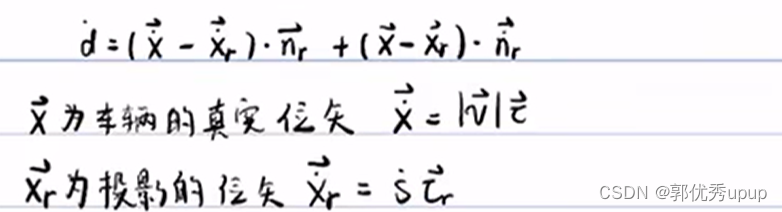
向量求导基本概念解释如下:

上图中最后的等式是dr与ds大小趋近于相等,也就是说它两是等价无穷小, 其中τ是r的切线方向的单位向量。
可以进一步的写成如下:

同样的对于nr来说一样有:

其中ds/dt是s点,其中dnr/ds要根据向量微积分frenet公式![]() (其中k是曲率)进行变换,带入可得
(其中k是曲率)进行变换,带入可得![]() 。进一步将d点化成下面这样,其中τr和nr向量垂直,内积是0,x-xr就是nr乘d,结果如下:
。进一步将d点化成下面这样,其中τr和nr向量垂直,内积是0,x-xr就是nr乘d,结果如下:

由 可进一步得到
可进一步得到![]() ,这样就可以建立起来d点与v、θ和θr之间的关系。
,这样就可以建立起来d点与v、θ和θr之间的关系。
算S点,还是使用式子![]() 这个关系来求,两边进行求导可得:
这个关系来求,两边进行求导可得:
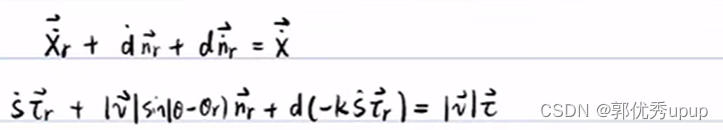
对其进行两边同时点乘以τ可得(τ·τ=1;τ·n=0):

最终可得:

这两个公式十分重要,无人驾驶理论的起点,其中θ是航向角,但是上面的公式和vy还有φ没有直接联系,将θ=φ+β带入可得:


使用同样的方法可将s点也化成与vx和vy的形式,但是s点是纵向控制的内容。到这里就已经将d与φ和vy联系起来了。
d是横向误差,![]() ,因为航向误差应该是θ-θr,也就是φ+β-θr,但这里φ是横摆角。
,因为航向误差应该是θ-θr,也就是φ+β-θr,但这里φ是横摆角。
可以将上面的公式改写成下面这样:
![]() 这里假设vx是一个常数。
这里假设vx是一个常数。
![]() 这里将θr两点是一个较小量,可以将它省略去,因为一般道路的曲率很小,
这里将θr两点是一个较小量,可以将它省略去,因为一般道路的曲率很小,![]() ,不会特别曲折,所以对于θr我们只考虑到一阶导数位置,二阶可以直 接判断它是一个较小量忽略。可进一步引出下面的微分方程组:
,不会特别曲折,所以对于θr我们只考虑到一阶导数位置,二阶可以直 接判断它是一个较小量忽略。可进一步引出下面的微分方程组:
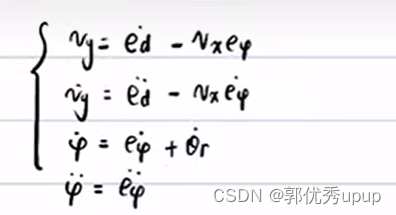
将上面的微分方程组带入到之前推导出来的二自由度车辆动力学模型中可得:\


上面的两个方程就是把原来和vy与φ有关的车辆动力学方程转化成误差的微分方程。将其简写成以下这样的形式,写成线性微分方程组的形式:


这样就通过坐标变换和车辆动力学方程将误差微分方程组建立起来了。

使用LQR对建立的模型对模型进行控制
下面使用一个离散型的LQR来选出一个合适的u使得误差最小,如下:

使用dlqr就延伸出来两个问题:

离散化的方法有:①向前欧拉法;②中点欧拉法 ;
(1)向前欧拉法

不同的方法对ξ的解释不同,如下:
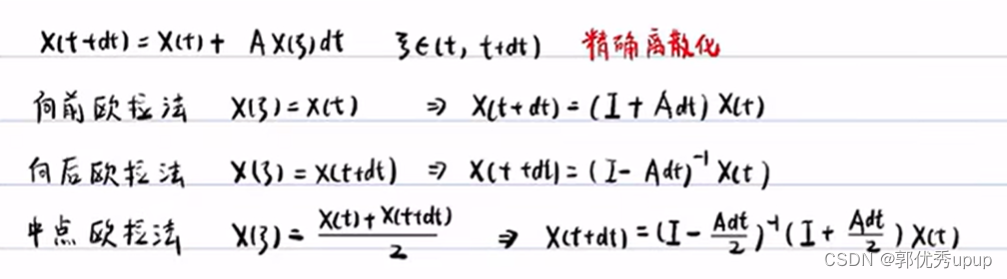
向前欧拉法认为X(ξ)=X(t);向后欧拉法认为X(ξ))=X(t+dt); 中点欧拉法认为是X(ξ)=[X(t)+X(t+dt)]/2。其中中点欧拉法精度要比向前和向后精度要高一点。
回到本例子中,X(ξ)使用中点欧拉法,u(ξ)使用向前欧拉法,因为u(t+dt)未知。如下:

最后一步中u(t)的系数中省略了![]() ,是因为dt时间间隔是一个较小量,这样可以简化运算,进一步可以将上式子写成如下形式:
,是因为dt时间间隔是一个较小量,这样可以简化运算,进一步可以将上式子写成如下形式:
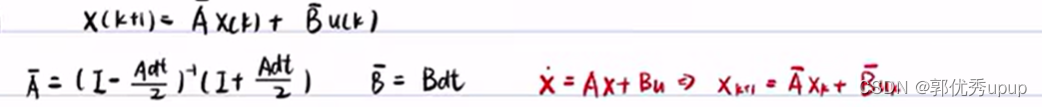
系统离散后的方程如上式子。下面使用dlqr进行求解

这里的A对应于上面的A杠,B对应于上面的B杠。将∞写成n,使n趋于∞,具体做法如下:

这里没有没有Un的转置乘以R再乘以Un的原因是由约束决定的,Xn就是要比Un多一项,如下:
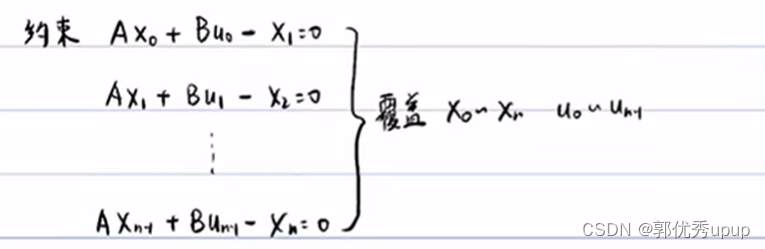
理解了为什么没有 Un的转置乘以R再乘以Un,使用拉格朗日乘子法写出最终的代价函数,如下:
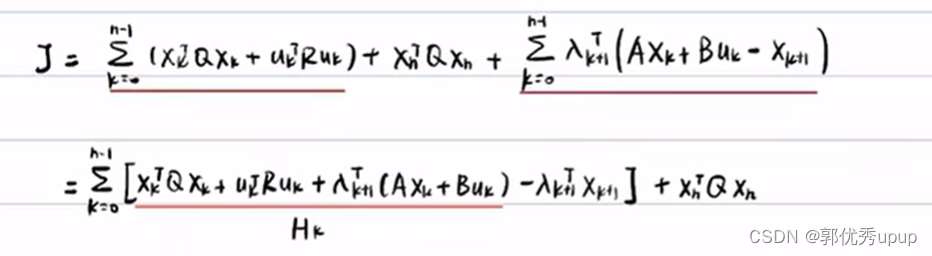

代价函数对各变量求偏导,有:

最终算出得到的是:

上面的式子由式②中R和B已知,但是λk+1未知,如果算出λk+1已知,那么就可以求出uk。由式④中可可知λn和Xn有关,Xn是已知的,那么λn也就已知了,可由式③和式①逆推出λn-1,是最从最末端n往前逆推的。逆推关系如下:
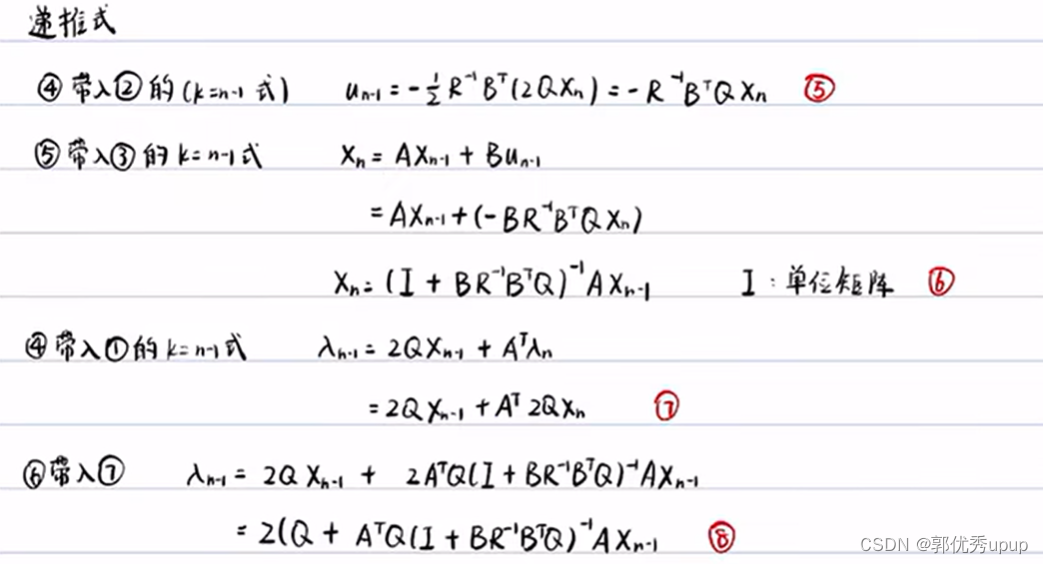
将⑧式与④式进行比较,可以发现⑧式也可以写成![]() 的形式。
的形式。
![]() 可以将求解λk的问题转换成求解Pk的问题。因为由式②可知uk和λk+1直接相关,只要求出Pk+1,就可以求出λk+1,进而求出uk。接下来求Pk。
可以将求解λk的问题转换成求解Pk的问题。因为由式②可知uk和λk+1直接相关,只要求出Pk+1,就可以求出λk+1,进而求出uk。接下来求Pk。

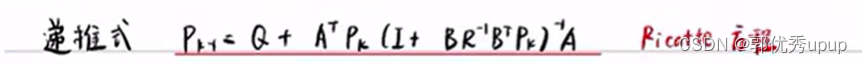
黎卡提方程在迭代几十次之后一般就会收敛与某一个常值,对于求解是很有帮助的,不用迭代无数次。也就是迭代一定次数后,黎卡提方程实际上是
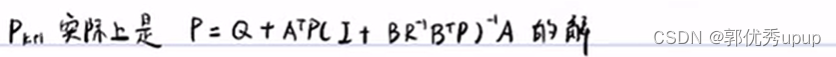
由上面的黎卡提方程可知:Pn=Q,再由Pn进而递推到Pn-1,依次类推。Pk得到后,Uk就已知了:
所以最终步骤是P先取初值Q,在带到黎卡提方程中进行迭代,P收敛之后再将其带入到u的表达式中![]() ,其中K=
,其中K=![]() 。
。
在matlab中lqr的包是![]() 。输入是A、B、Q、R,就可以计算出k、S、E。在有的书上黎卡提是写成
。输入是A、B、Q、R,就可以计算出k、S、E。在有的书上黎卡提是写成 ,它其实是和上面的黎卡提方程式一样的,可根据矩阵求逆引理转换:
,它其实是和上面的黎卡提方程式一样的,可根据矩阵求逆引理转换:

一般推荐使用下面的黎卡提方程,也就是![]() ,因为使用这个形式的黎卡方程后半部分(R+BTPB)-1是一个1×1的矩阵求逆,但是使用上面的黎卡提方程,也就是
,因为使用这个形式的黎卡方程后半部分(R+BTPB)-1是一个1×1的矩阵求逆,但是使用上面的黎卡提方程,也就是![]() ,这形式后半段(I+BR-1BTPk)-1是一个4乘4的矩阵,相对而言上面的1×1矩阵来说不好求逆。
,这形式后半段(I+BR-1BTPk)-1是一个4乘4的矩阵,相对而言上面的1×1矩阵来说不好求逆。
对LQR算法进行总结:

勘误:这里的k的值是: ![]()
LQR的核心就是求解黎卡提方程,求出P之后就可以求出最优的控制量U;如果系统是连续的,可以使用连续LQR算出K出来,也可以将这个连续系统离散化再使用离散LQR算出K值,这两个K值应该是非常接近,但是不可能完全一样。将u=-kx这样的控制称为全状态反馈控制。
前馈控制
这里加前馈控制是为了解决之前上面忽略掉的![]() Cθr点。没有前馈只有反馈控制的话,也就是只用LQR的话,如下:
Cθr点。没有前馈只有反馈控制的话,也就是只用LQR的话,如下:
只有LQR控制时,err和err点不可能同时为0,当P经过一定迭代次数后会稳定下来,u=-kx也是一个固定的值,此时err点=0,err≠0。引入前馈控制可以消除稳态误差。

由LQR引起的稳态误差是:
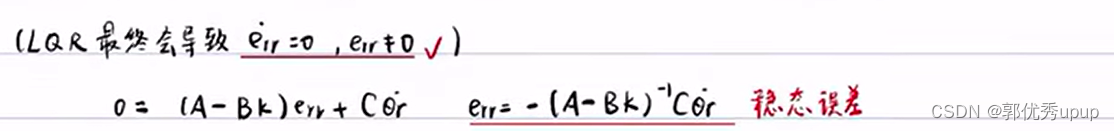
引入前馈控制后:
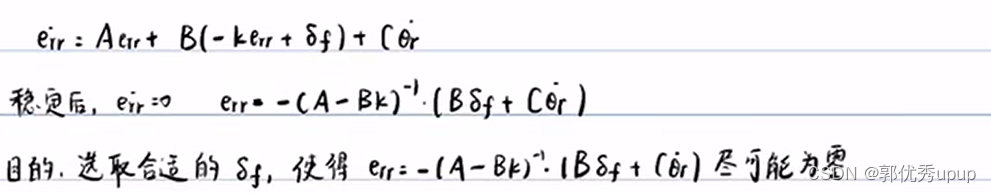
这里需要注意B是一个列向量,不能求逆,所以求解δf时不能简单的是·。可以借助数学软件进行求解。求解出来的err如下所示:
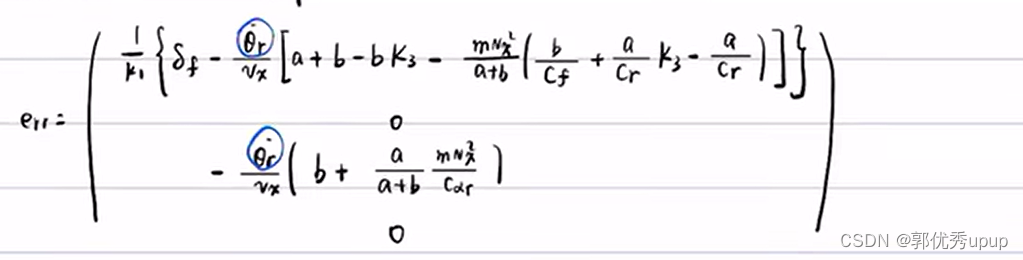
进而可以求解出来δf
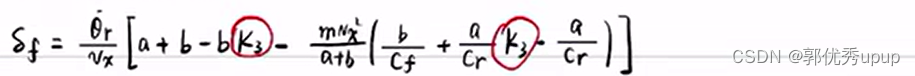
其中k3是反馈矩阵K=(k1,k2, k3, k4)中的k3,所以前馈δf的计算是依赖于反馈中的K矩阵,所以要先算反馈,再算前馈。
由上面求解出来的err矩阵可得:

可知eφ于δf和k的影响,也就是无论前馈和反馈取何值,eφ≠0。前面学习学习过eφ=φ-θr,它不是航向误差,航向误差是φ+β-θr,所以eφ=φ-θr的稳态误差应该是β。接下来要看这个式子是不是β。如下:

使用ed=φ-θr化简后有![]() 。
。
曲线曲率的定义是dθ/ds,![]() ,所以
,所以![]() ,在实际规划的路径中道路的曲率的绝对值是远远小于1,
,在实际规划的路径中道路的曲率的绝对值是远远小于1,![]() ,可对S点进行简化,
,可对S点进行简化,![]() (这里vy是一个小量,sineφ也是一个小量,相乘是一个高阶的小量,可以将其近似成0)。所以
(这里vy是一个小量,sineφ也是一个小量,相乘是一个高阶的小量,可以将其近似成0)。所以![]() ,再将其带入到eφ中可得:
,再将其带入到eφ中可得:

之前在上面讲过 ,无漂移时vy远远小于1,是一个较小量,如下:
,无漂移时vy远远小于1,是一个较小量,如下:

在将其带入到上一步改写的eφ当中去可得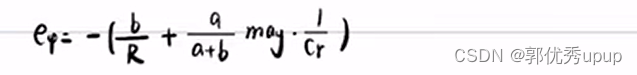
由以下关系进一步化简:

可进一步化简:
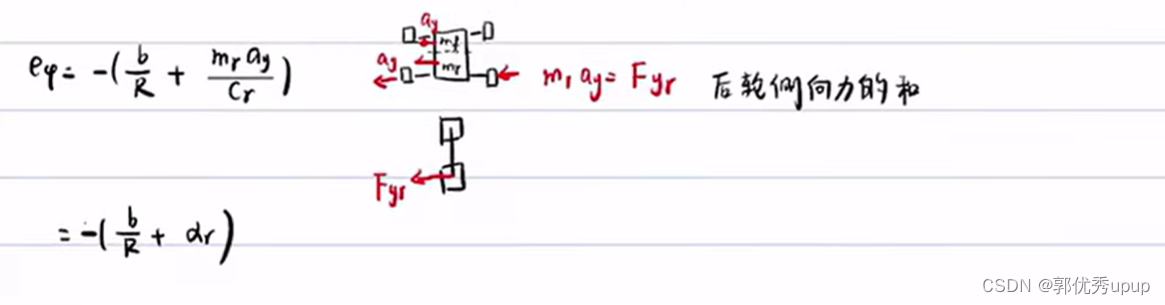
其中mr是车辆后半部分的质量,Fy是后轮侧向力之和。mray就是单个后轮的侧向力,Cr是侧偏刚度,所以αr是后轮的侧偏角。
还可以进一步化简:
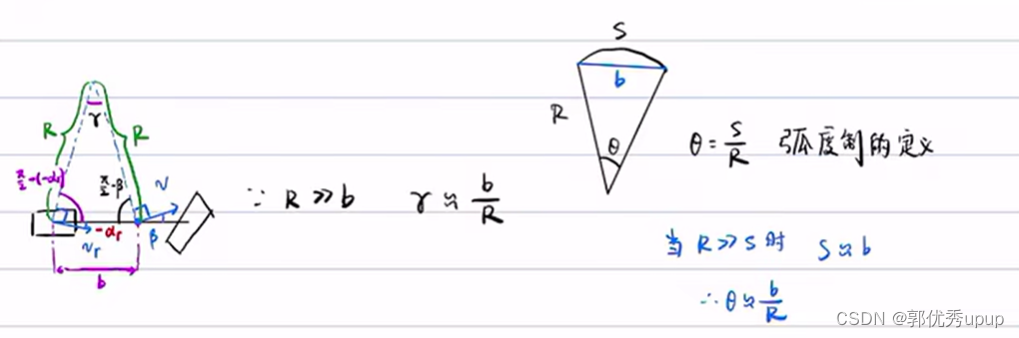
由于转弯半径很大,所以绿色部分可以近似看出是转弯半径,紫色的长度是后轴轴距到质心的距离,转弯半径是远远大于b的,所以γ=b/R,(弧度制定义)。
 至此证得eφ就等于-β。
至此证得eφ就等于-β。


所以只需要用前馈控制把横向误差ed趋近于0就可以,前馈δf就是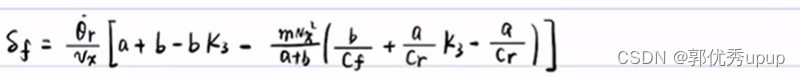
令θr=kvx可进一步化简:
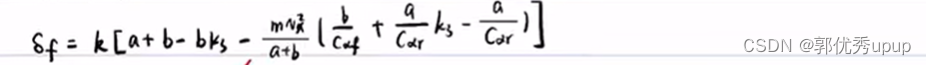
最后可以算出u:
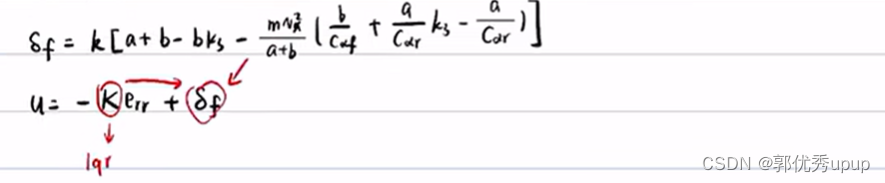
通过LQR和前馈控制就可以将横向误差控制为 。
。
离散轨迹的误差计算
由上一节可知各个横向误差的计算公式:
 从上面的式子可以看出计算误差时都需要知道投影点的信息,如下:
从上面的式子可以看出计算误差时都需要知道投影点的信息,如下:

剩下的几个自变量都是已知的,可以通过车辆的传感器获取到,如下:

所以只需要知道投影点信息就可以计算出误差:、

这里需要需要注意如果规划出来的路径是连续的,可能会导致投影点不唯一,如下:
如果轨迹比较简单,则投影点唯一,如图1和图2,如果规划出来的路径较为复杂时,投影点就可能不唯一:
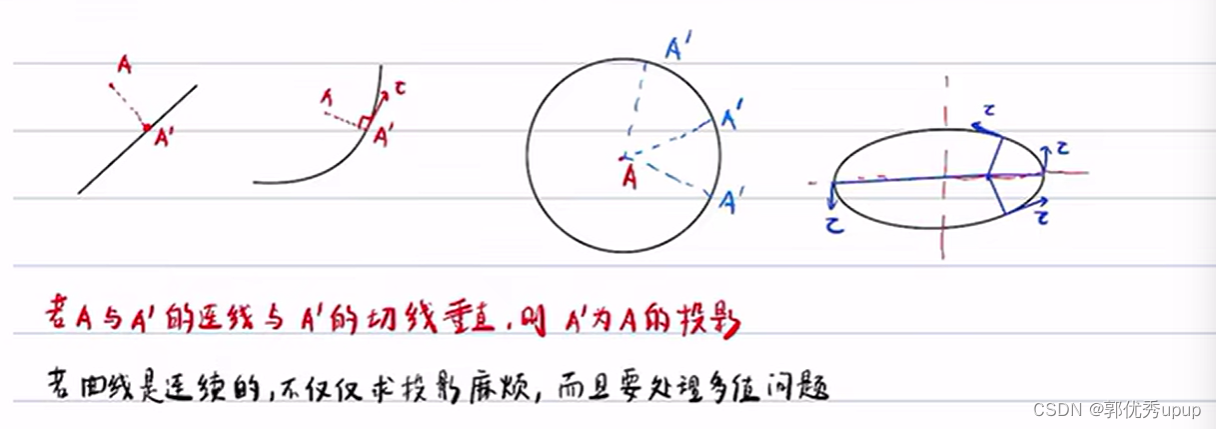
所以如果曲线是连续的话,求投影点可能会很麻烦,并且要处理多值问题,所以使用离散的规划点会容易很多,使用离散轨迹点的误差计算步骤如下:

每个离散的规划点上的信息(xm,ym,θm,km)都是已知的,所以x-xm这个向量是已知的,需要求的是ed。

τm轨迹切向的向量,坐标点位置是(cosθm,sinθm),nm轨迹法向的向量,坐标点位置是(-sinθm,cosθm)。ed近似于x-xm在法向方向上的分量,也就是向量x-xm在nm上的投影,计算方法就是[(x-xm)·nm]/|nm|,由于这里的nm是单位向量,其模为1,所以最终结果就是(x-xm)·nm。
es近似于x-xm这两个向量相减在切向方向上的分量。这种近似是在曲率等于0时,是没有误差的,意味着规划出的轨迹是直线的话,只需要很少的规划点,在曲率比较大的轨迹出需要比较密的规划点。



横向控制算法和流程图
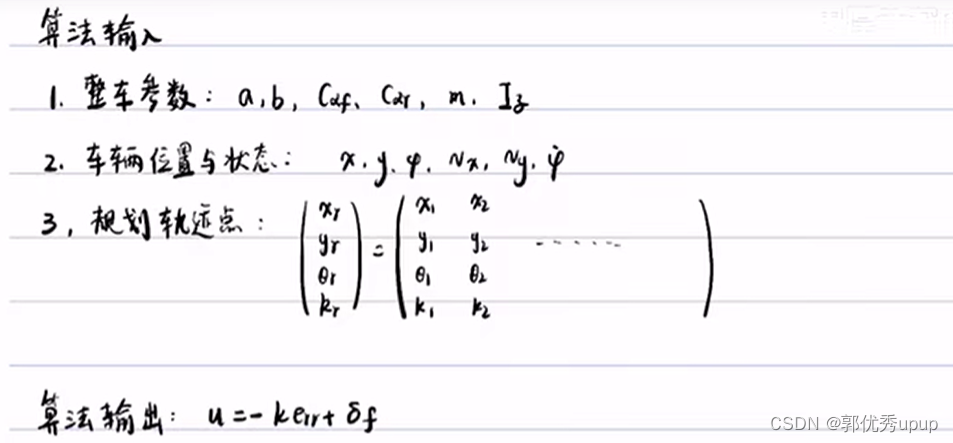

流程图如下:
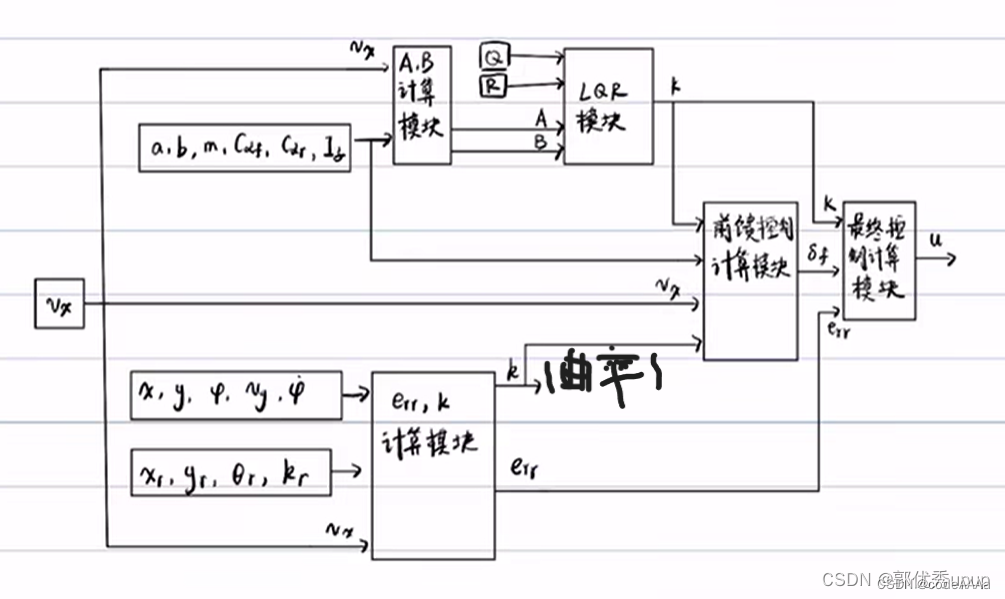
其中大K是LQR计算出来的K值,小k是真实的车在规划轨迹上的投影点的曲率。
具体的算法:



在自动驾驶实际应用中,对实时性要求很高,一般不是掉包计算出来的吗,都是查表查出来的,这是一种空间换时间的例子。 在低速情况下,轮胎的侧偏刚度变换不大,大K的计算主要考虑vx的值这个表就是一个一维的表(查vx算K,进而求解LQR),这个查表法同样适合高速情况,在高速情况下,轮胎侧偏刚度变换大,就需要考虑轮胎侧偏刚度和vx,此时就是根据vx和侧偏刚度来求解大K(表就是一个三维的表)。
第三步是重中之重:


其中容易出出错的是第九步,因为φ加上一个2π还是φ,θr加上一个2π还是θr,但是eφ加上2π就会出现一个很大的幅度,导致控制失效。
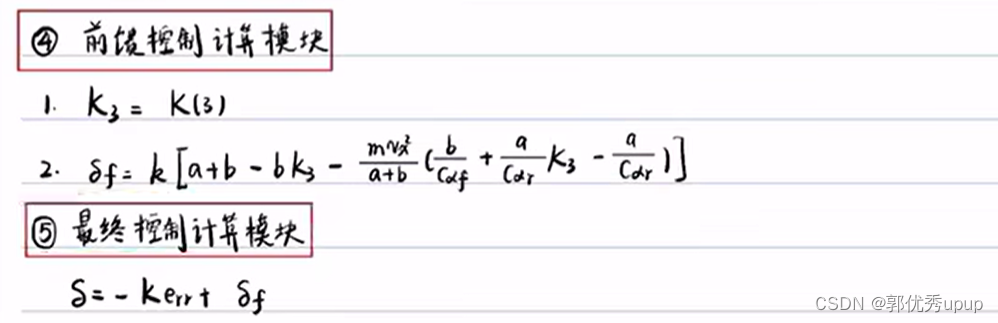
有了上面五个模块,还要有一个预测模块,因为车辆的运动本身会有惯性,还有就是例如下面的情况:
上面的第二种情况,算法控制是方向盘不会动,它只有在下一个时刻知道有误差时才会动方向盘,但是没有预测模块时,它在当前时刻是不会改变方向盘的转角的,所以算法控制时具有一定的滞后性。
当加了预测模块的算法框图:

其中小k是真实车在规划的轨迹上的投影点的曲率。K就是LOR计算出来的。
上述两种情况加了预测后,如下:

如果没有预测时,d不为零,那么u不等0,方向盘转角会发生改变,如果有预测,比如预测点是xpre,该预测点与轨迹重合,u=0,就不打方向盘。

绿色点是预测的点,此时预测点和规划的轨迹不重合,有距离d,所以会打方向盘。
预测算法写法:

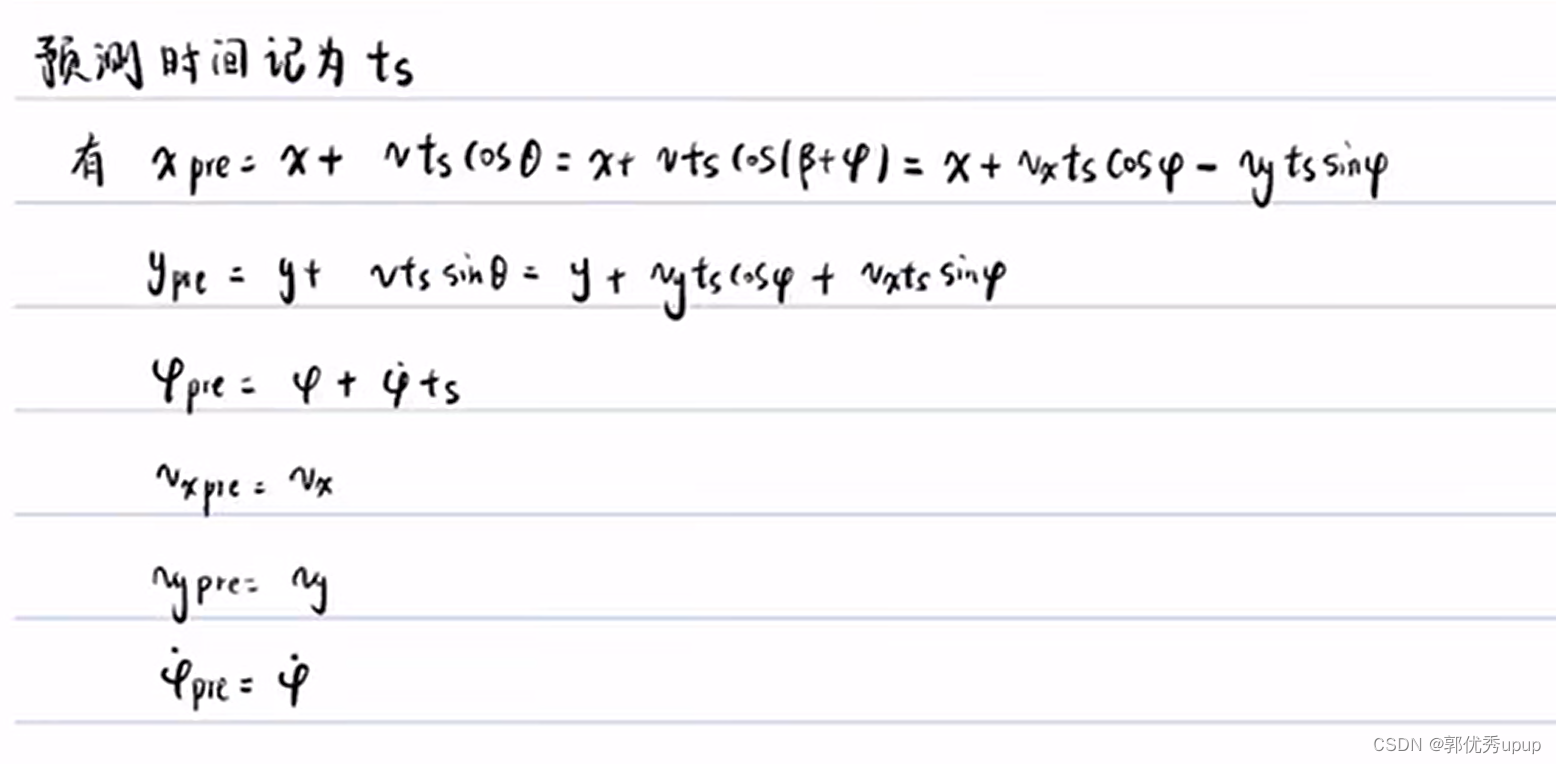




![[iOS]组件化开发](https://img-blog.csdnimg.cn/direct/f37a3b1d57174d01ae104218fa1b11d3.png)