两种类型的二叉搜索树

news2024/10/6 16:23:37

文章目录

  • 1.搜索二叉树的概念
  • 2.搜索二叉树的模拟实现
    • 2.1 搜索二叉树的结构
    • 2.2 插入
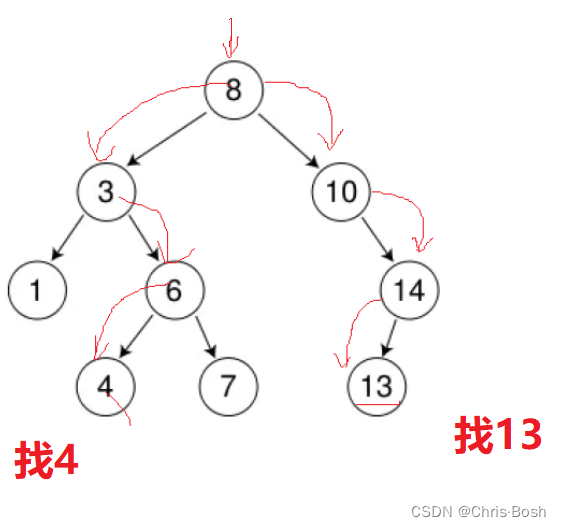
    • 2.3 查找
    • 2.4 删除
    • 2.5 中序遍历
    • 2.6 完整代码
  • 3.二叉搜索树的两种模型
    • 3.1 两种模型
    • 3.2 key_value模型搜索二叉树
  • 4.两种二叉树的测试

1.搜索二叉树的概念

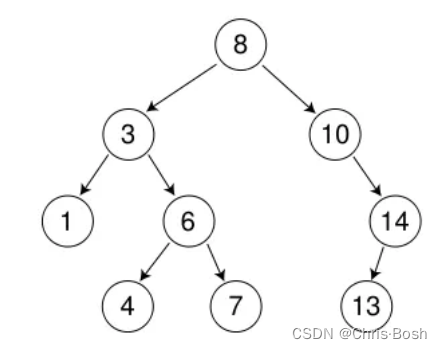
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:
①若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
②若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
③它的左右子树也分别为二叉搜索树
下面便是一个例子：
在这里插入图片描述

2.搜索二叉树的模拟实现

2.1 搜索二叉树的结构

template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}

2.2 插入

bool Insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}
			//找插入位置
			Node* parents = nullptr;
			Node* cur = _root;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					parents = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			//插入
			cur = new Node(key);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			return true;
		}

在这里插入图片描述

2.3 查找

bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return true;
				}
			}
			return false;
		}

在这里插入图片描述

2.4 删除

bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
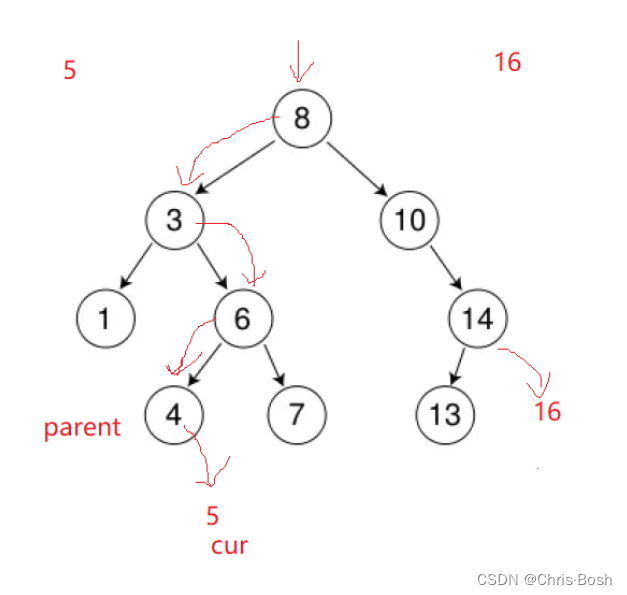
					//找到节点后准备删除，有三种情况
					//1.第一种情况
					if (cur->_left == nullptr)// 左为空，父亲指向我的右
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					//2.第二种情况
					else if (cur->_right == nullptr)// 右为空，父亲指向我的左
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{					
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
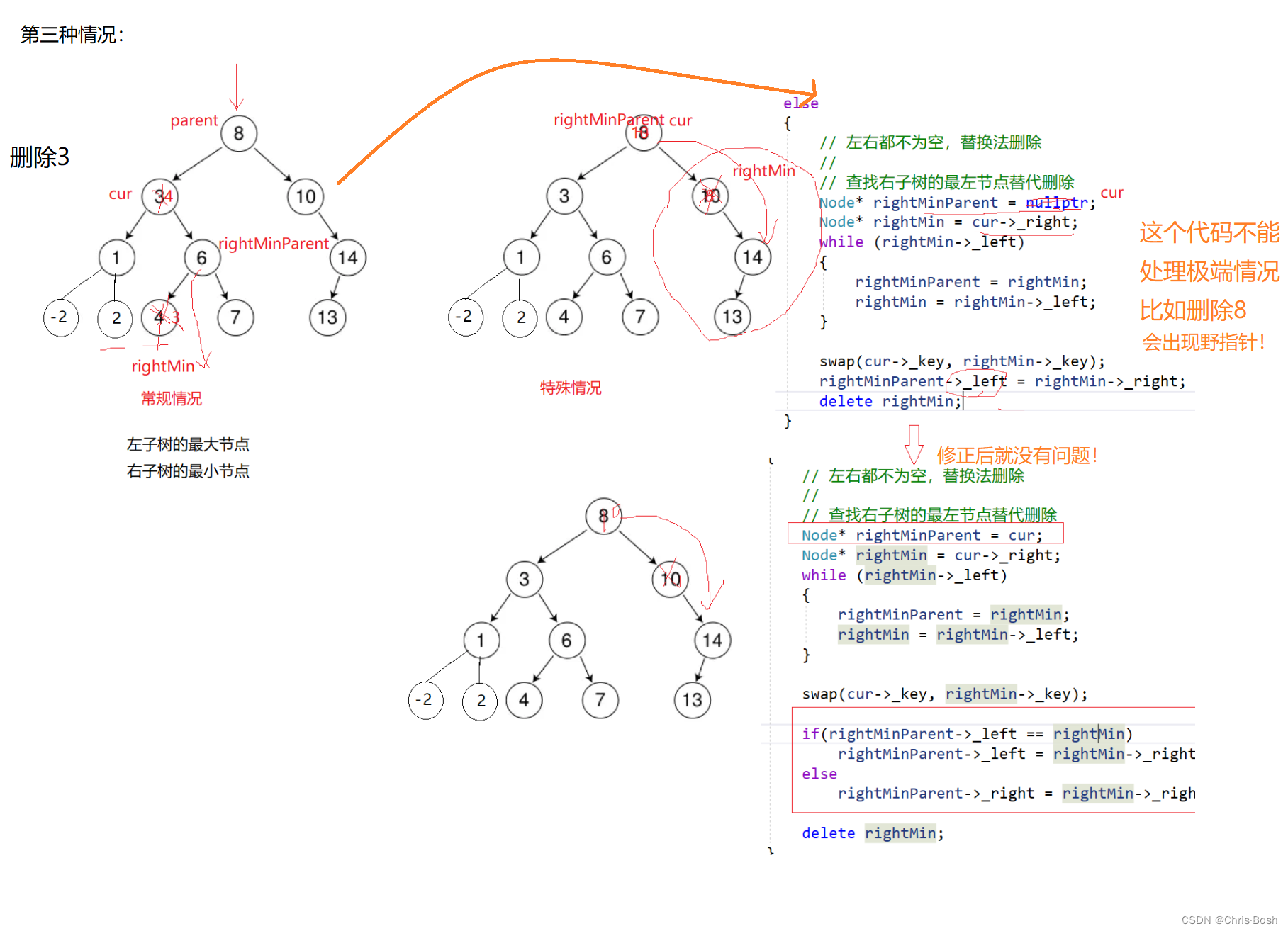
					//3.第三种情况
					else
					{
						// 左右都不为空，替换法删除
						// 查找右子树的最左(小)节点替代删除
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)//找右子树的最小节点
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						swap(cur->_key, rightMin->_key);
						if (rightMinParent->_left == rightMin)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;

						delete rightMin;
					}
					return true;
				}
			}
		}

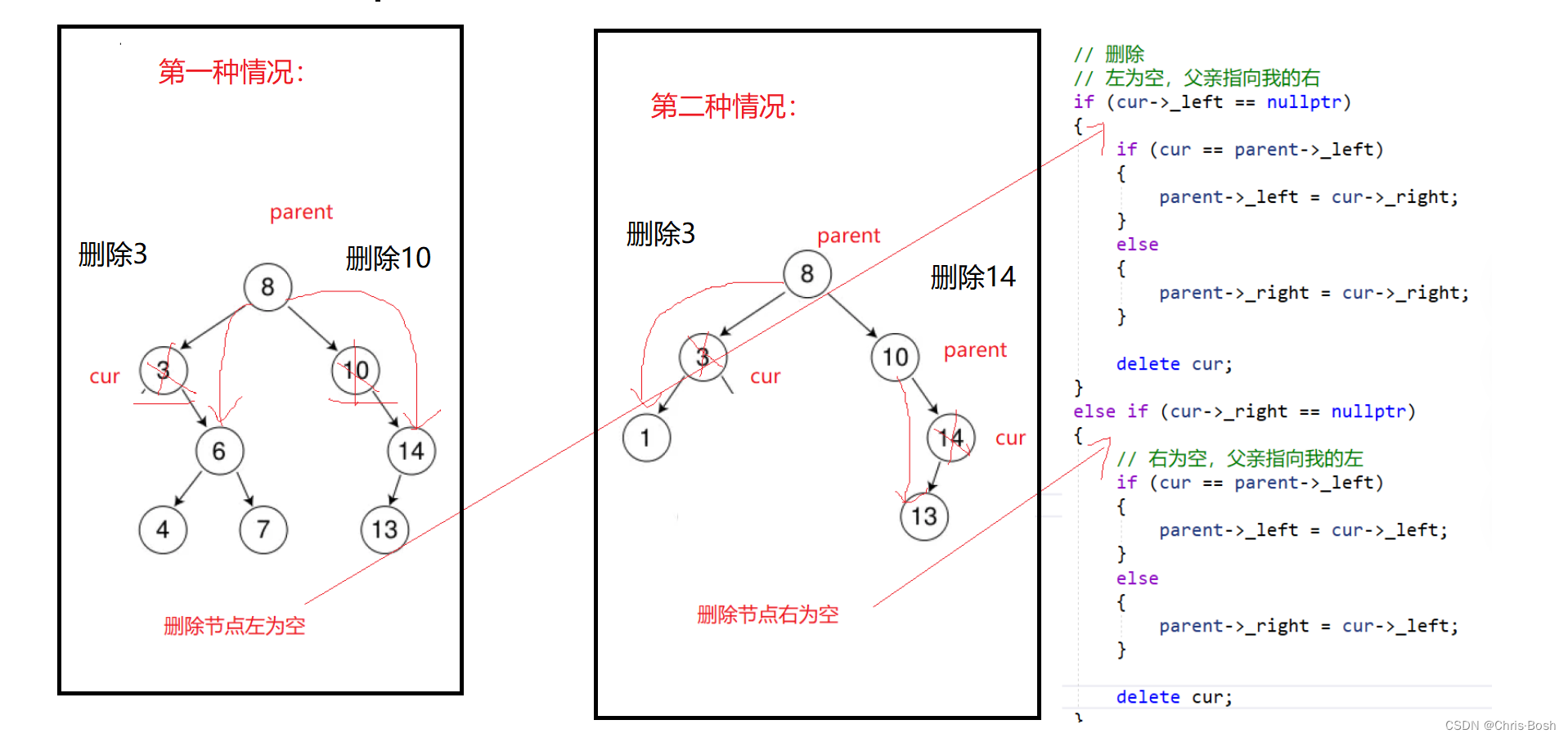
在这里插入图片描述

第三种情况替换遵守一个个规则： 替换要找左子树的最大节点 或者右子树的最小节点 在这里插入图片描述

2.5 中序遍历

        void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}

2.6 完整代码

#pragma once
#include<string>

namespace key
{
	template<class K>
	struct BSTreeNode
	{
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;

		BSTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};


	template<class K>
	class BSTree
	{
		typedef BSTreeNode<K> Node;
	public:
		bool Insert(const K& key)
		{
			if (_root == nullptr)
			{
				_root = new Node(key);
				return true;
			}
			//找插入位置
			Node* parents = nullptr;
			Node* cur = _root;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					parents = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}
			//插入
			cur = new Node(key);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			return true;
		}

		bool Find(const K& key)
		{
			Node* cur = _root;
			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return true;
				}
			}
			return false;
		}

		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur != nullptr)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					//找到节点后准备删除，有三种情况
					//1.第一种情况
					if (cur->_left == nullptr)// 左为空，父亲指向我的右
					{
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					//2.第二种情况
					else if (cur->_right == nullptr)// 右为空，父亲指向我的左
					{
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{					
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					//3.第三种情况
					else
					{
						// 左右都不为空，替换法删除
						// 查找右子树的最左(小)节点替代删除
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)//找右子树的最小节点
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						swap(cur->_key, rightMin->_key);
						if (rightMinParent->_left == rightMin)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;

						delete rightMin;
					}
					return true;
				}
			}
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}
			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}
	private:
		Node* _root = nullptr;
	};
}

3.二叉搜索树的两种模型

3.1 两种模型

①K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。

也就是上面的那种情况。

②KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。

2.1比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英
文单词与其对应的中文<word, chinese>就构成一种键值对；
2.2再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对

3.2 key_value模型搜索二叉树

#pragma once
#include<string>
#include<iostream>
using namespace std;


namespace key_value
{
	template<class K, class V>
	struct BSTreeNode
	{
		BSTreeNode<K, V>* _left;
		BSTreeNode<K, V>* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}
	};

	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}
			//找插入位置
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key, value);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}
			return true;
		}

		Node* Find(const K& key)//为了返回对应值value值的节点，要修改原来的bool类型
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}
			return cur;
		}

		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					// 删除
					// 左为空，父亲指向我的右
					if (cur->_left == nullptr)
					{
						//if(parent == nullptr)
						if (cur == _root)
						{
							_root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}

						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						//if(parent == nullptr)
						if (cur == _root)
						{
							_root = cur->_left;
						}
						else
						{
							// 右为空，父亲指向我的左
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}

						delete cur;
					}
					else
					{
						// 左右都不为空，替换法删除
						// 
						// 查找右子树的最左节点替代删除
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}

						swap(cur->_key, rightMin->_key);

						if (rightMinParent->_left == rightMin)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;

						delete rightMin;
					}

					return true;
				}
			}
			return false;
		}

		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << ":" << root->_value << endl;
			_InOrder(root->_right);
		}

		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

	private:
		Node* _root = nullptr;
	};
}

4.两种二叉树的测试

test.cpp:

#define _CRT_SECURE_NO_WARNINGS 1
#include "BStree(k).h"
#include"BStree(kv).h"

int main()
{
	key::TestBSTree1();
	cout << "-----------------------------------------------------------------" << endl;
	key_value::TestBSTree();
	return 0;
}

key搜索二叉树：

void TestBSTree1()
	{
		int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
		BSTree<int> t1;
		for (auto e : a)
		{
			t1.Insert(e);
		}

		t1.InOrder();

		//t1.Erase(3);
		t1.Erase(8);

		t1.InOrder();

		for (auto e : a)
		{
			t1.Erase(e);
			t1.InOrder();
		}
	}

key_value搜索二叉树：

void TestBSTree()
	{
		string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };
		// 统计水果出现的次
		BSTree<string, int> countTree;
		for (auto str : strs)
		{
			auto ret = countTree.Find(str);
			if (ret == NULL)
			{
				countTree.Insert(str, 1);
			}
			else
			{
				ret->_value++;
			}
		}
		countTree.InOrder();


		cout << "请输入英文单词，如果词典中有该单词，则输出该单词的中文；如果词库没有，则输出'单词拼写错误'\n";
		BSTree<string, string> dict;
		dict.Insert("insert", "插入");
		dict.Insert("erase", "删除");
		dict.Insert("left", "左边");
		dict.Insert("string", "字符串");

		string str;
		while (cin >> str)
		{
			auto ret = dict.Find(str);
			if (ret)
			{
				cout << str << ":" << ret->_value << endl;
			}
			else
			{
				cout << "单词拼写错误" << endl;
			}
		}
	}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1632612.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Canvas与艺术】 绘制五星红旗

【Canvas与艺术】 绘制五星红旗

【注意】 该图中五星定位和大小都是按 https://www.douyin.com/note/7149362345016380710 精确绘制的。 【成图】 【代码】 <!DOCTYPE html> <html lang"utf-8"> <meta http-equiv"Content-Type" content"text/html; charsetutf-8&q…
阅读更多...
[iOS]组件化开发

[iOS]组件化开发

一、组件化开发基础 1.组件定义 在软件开发中&#xff0c;一个组件是指一个独立的、可替换的软件单元&#xff0c;它封装了一组相关的功能。组件通过定义的接口与外界交互&#xff0c;并且这些接口隔离了组件内部的实现细节。在Swift语言中&#xff0c;组件可以是一个模块、一…
阅读更多...
Qt使用OPCUA

Qt使用OPCUA

假如想在Qt下使用OPCUA通讯&#xff0c;貌似大家都是倾向于使用【qtopcua】这个库。但是在Qt6之前&#xff0c;假如想使用这个库&#xff0c;还得自己编译&#xff0c;比较繁琐。假如想开箱即用&#xff0c;而且没有使用太复杂的功能的话&#xff0c;其实可以直接使用open62541…
阅读更多...
项目：使用LNMP搭建私有云存储

项目：使用LNMP搭建私有云存储

目录 项目&#xff1a;使用LNMP搭建私有云存储 准备工作 回复快照&#xff0c;关闭安全软件 上传软件 设置nextcloud安装命令权限 设置数据库 重启数据库 配置nginx 安装 内网穿透 cpolar的域名信任 项目&#xff1a;使用LNMP搭建私有云存储 准备工作 回复快照&a…
阅读更多...
Word插件开发

Word插件开发

VSTO是Visual Studio Tools for Office的简称&#xff0c;它是Microsoft Visual Studio的一个扩展&#xff0c;用于开发基于Microsoft Office平台的应用程序。VSTO提供了一套API和工具&#xff0c;使开发人员能够利用Visual Studio IDE来开发定制的Office解决方案。 在 Visual…
阅读更多...
MySQL中的数据类型及一些应用场景

MySQL中的数据类型及一些应用场景

1.6. 数据类型 MySQL的数据分为以下几个大类&#xff1a; 1. String Types 字符串类型 2. Numeric Types 数字类型 3. Date and Time Types 日期和时间类型 4. Blog Types 存放二进制的数据类型 5. Spatial Types 存放地理数据的类型 1.6.1. 字符串类型 最常用的两个字符串类…
阅读更多...
Odoo：世界排名第一的免费开源设备资产（EAM）管理系统介绍

Odoo：世界排名第一的免费开源设备资产（EAM）管理系统介绍

本文节选自Odoo亚太金牌服务机构【开源智造】所编写的《Odoo行业应用解决方案白皮书》如需获取完整的知识内容&#xff0c;请至开源智造官网免费获取。感谢网友一键三连&#xff1a;点赞、转发、收藏&#xff0c;您的支持是我们最大的前进动力&#xff01; 概述 实施全面的维护…
阅读更多...
免费语音转文字：自建Whisper，贝锐花生壳3步远程访问

免费语音转文字：自建Whisper，贝锐花生壳3步远程访问

Whisper是OpenAI开发的自动语音识别系统&#xff08;语音转文字&#xff09;。 OpenAI称其英文语音辨识能力已达到人类水准&#xff0c;且支持其它98中语言的自动语音辨识&#xff0c;Whisper神经网络模型被训练来运行语音辨识与翻译任务。 此外&#xff0c;与其他需要联网运行…
阅读更多...
AI 工具合集

AI 工具合集

以下工具来源于互联网&#xff0c;可能会失效&#xff0c;请参考使用 网红工具 名称链接说明GPT-4https://chat.openai.com/ 需要梯子&#xff0c;需要付费。功能最强大的聊天机 器人。 文心一言https://yiyan.baidu.com/welcome 国内版 GPT&#xff0c;需要申请账号。回答问…
阅读更多...
React的状态管理useState

React的状态管理useState

基础使用 useState 是一个 React Hook&#xff08;函数&#xff09;&#xff0c;它允许我们向组件添加一个状态变量, 从而控制影响组件的渲染结果和普通JS变量不同的是&#xff0c;状态变量一旦发生变化组件的视图UI也会跟着变化&#xff08;数据驱动视图&#xff09; useState…
阅读更多...
C++：常函数

C++：常函数

在C中&#xff0c;常函数&#xff08;const member functions&#xff09;是指在类的成员函数声明和定义中使用 const 关键字修饰的函数。常函数的存在主要是为了在类的实例上提供一种保证&#xff1a;该函数不会修改类的成员变量。 在类的成员函数声明中&#xff0c;如果函数…
阅读更多...
2024年CMS市场的份额趋势和使用统计

2024年CMS市场的份额趋势和使用统计

目前市面上有超过一半的网站都是使用CMS来搭建的&#xff0c;据不完全统计&#xff0c;现在大概有900多种CDM可供选择&#xff0c;以下是最常见的CMS的市场份额和使用率信息&#xff1a; 除了WordPress以外&#xff0c;Shopify和Wix也是比较流行的内容管理系统&#xff0c;尤其…
阅读更多...
面试集中营—ElasticSearch架构篇

面试集中营—ElasticSearch架构篇

一、为什么用ElasticSearch&#xff1f; 1、支持多种数据类型。它可以处理非结构化、数值和地理信息等多种类型的数据&#xff1b; 2、简单的RESTful API。ES提供了一个简单易用的RESTful API&#xff0c;使得它可以从任何编程语言中调用&#xff0c;降低了学习的曲线。 3、近实…
阅读更多...
HUST华科校园网自动登录

HUST华科校园网自动登录

HUST校园网开机自动登录&#xff0c;后台保活 校园网虽然有无感认证&#xff0c;但是每次还得弹出网页&#xff0c;再点击一次连接&#xff0c;还是挺麻烦的。而且对于一部分开机自启的联网app来说&#xff0c;每次开机后无网络可能导致某些应用功能出bug或者其他异常行为。因此…
阅读更多...
笃行致远，“易”往无前 | 易保全成立10周年啦

笃行致远，“易”往无前 | 易保全成立10周年啦

日月其迈&#xff0c;岁律更新。2024年4月28日&#xff0c;易保全迎来了10周岁生日。10年磨一剑&#xff0c;易保全创立至今&#xff0c;始终坚定自己的初心和使命&#xff0c;在时代的激流勇进中&#xff0c;以电子数据保全机构的身份与中国区块链共成长。 “创”说十年&…
阅读更多...
Blender常见操作

Blender常见操作

1.局部视图&#xff1a;Local View&#xff0c;也可称作Solo模式&#xff0c;按快捷键 “/”进入&#xff0c;在按退出&#xff0c;只显示选中的物体&#xff08;可多选&#xff09;&#xff0c;方便编辑 2.物体合并&#xff1a;Ctrl J 其中&#xff0c;当选中多个物体时&am…
阅读更多...
CSS border边框（理解网页边框制作）

CSS border边框（理解网页边框制作）

目录 一、border边框介绍 1.概念 2.特点 3.功能 4.应用 二、border边框用法 1.border边框属性 2.边框样式 3.边框宽度 4.边框颜色 5.边框-单独设置各边 6.边框-简写属性 三、border边框属性 四、border边框实例 1.创建带有阴影效果的边框&#xff1a; 2. 创建一个类似标…
阅读更多...
如何使用SOCKS5代理？

如何使用SOCKS5代理？

SOCKS5 是一个代理协议&#xff0c;在使用TCP/IP协议通讯的前端机器和服务器机器之间扮演一个中介角色&#xff0c;使得内部网中的前端机器变得能够访问Internet网中的服务器&#xff0c;或者使通讯更加安全。那么&#xff0c;SOCKS5代理该如何使用呢&#xff1f; 首先需要获取…
阅读更多...
Aiseesoft Blu-ray Player for Mac：蓝光播放器

Aiseesoft Blu-ray Player for Mac：蓝光播放器

Aiseesoft Blu-ray Player for Mac是一款功能强大且易于使用的蓝光播放器&#xff0c;专为Mac用户打造。它以其卓越的性能和简洁的操作界面&#xff0c;为用户带来了全新的高清蓝光播放体验。 Aiseesoft Blu-ray Player for Mac v6.6.50激活版下载 这款软件支持播放任何高质量的…
阅读更多...
2024年4月中国数据库排行榜：OceanBase再度登顶，KingBase稳步上升进前五

2024年4月中国数据库排行榜：OceanBase再度登顶，KingBase稳步上升进前五

春风劲吹&#xff0c;迎来了2024年4月中国流行度排行榜。纵观本月榜单&#xff0c;各家数据库产品你追我赶&#xff0c;名次呈现微妙变动&#xff0c;它们正以不可忽视的力量&#xff0c;推动着中国乃至全球的数据管理革新。在这春意盎然的四月&#xff0c;让我们继续关注这些数…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023