一. 直方图

方法1

	cv.calcHist(images, channels, mask, histSize, ranges=None, accumulate=False)
	参数:
		images: 输入图像，可以是单个图像或图像的列表
		channels: 
			计算直方图的通道
				对于灰度图像，该值为0
				对于RGB彩色图像，可以传递一个包含三个元素的数组 [0, 1, 2]，表示分别计算每个通道的直方图
		mask: 
			掩码图像，用于指定图像的哪个区域需要计算直方图
			如果不需要掩码，可以传递 None
		histSize:
			输出直方图的大小
				对于一维直方图，这是一个整数
				对于二维直方图，这是一个包含两个整数的元组
				对于三维直方图，这是一个包含三个整数的元组
		ranges: 
			可选参数，用于指定直方图的范围
			默认情况下，将使用图像的最小值和最大值
		accumulate: 
			可选参数，布尔值
				True:计算过程中将直方图累积到内部缓冲区中
	返回值：返回一个或多个计算出的直方图（取决于输入图像的数量）

方法2

	np.histogram(a, bins=10, range=None, normed=None, weights=None, density=None)
	参数:
		a: 输入数组
		bins: 可选参数，表示直方图的条形数（即分箱数量）,默认为10
		range: 
			可选参数，表示直方图的最小值和最大值范围，格式为 (min, max)
			如果未指定，则使用 a 的最小值和最大值
		normed: 可选参数，布尔值。
			 	如果为 True，则返回的直方图高度将归一化，使得直方图的面积为1
		weights: 
			可选参数，表示每个元素的重要性（权重）
			默认情况下，所有元素的权重都是1
		density: 
			可选参数，布尔值
			如果为 True，则返回的直方图高度将乘以 bins 的数量，使得直方图下的总面积等于1,这通常与 normed 一起使用
	返回值: 返回两个数组,即直方图的高度和区间边界的数组

方法3

	np.bincount(arr, weights=None, minlength=0)
	参数:
		arr:输入的一维整数数组
		weights:
			可选参数
			它是一个形状与arr相同的数组，用于给arr中的每个元素指定权重
				若提供了weights，则bincount将计算加权值的出现次数
		minlength: 
			可选参数
			指定了输出数组的最小长度
				若值 > 0的值，则当max(输入数组) < minlength时，输出数组将用0填充到指定的最小长度
	返回值:
		一个一维数组
			长度为max(arr)+1 / minlength(取决于哪个更大)

二. 掩码区域的直方图绘制

	1. 创建与原图一致的shape
	2. 创建mask区域
	3. 构建mask区域图像，cv.bitwise_and( )
	4. 计算直方图

三. 直方图均衡化

实际上一个比较好的图像像素点应该在某一范围内，而不是限制于某个特定的小范围，因此对像素的直方图可以进行拉伸操作

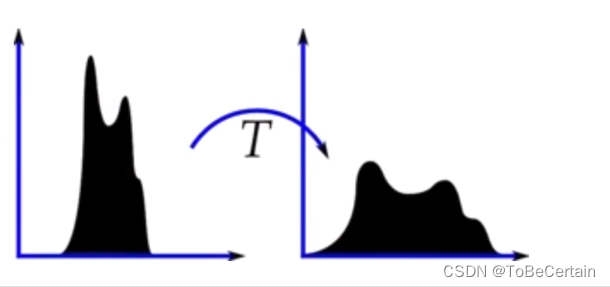
	比如：
	一个偏暗的图像，像素基本上都在较小的位置
		增大像素，图像变量

因此，直方图均衡化操作是一个提高图像对比度的方式

---

感谢阅读🌼
如果喜欢这篇文章，记得点赞👍和转发🔄哦！
有任何想法或问题，欢迎留言交流💬，我们下次见！
本文相关代码存放位置
    【Opencv 图像变换代码实现】

祝愉快🌟！

---