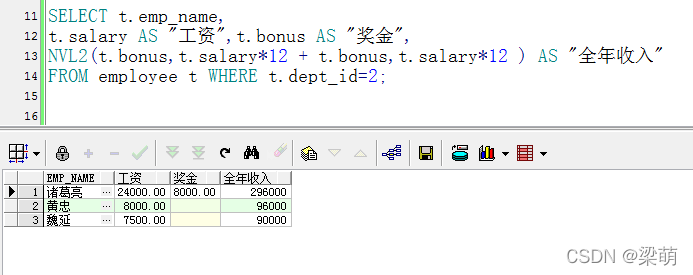
2-3树 -> 左倾红黑树
红黑树实际上是2-3树的一种基于BST的实现。普通二叉搜索树(BST)中的每一个节点,只有一个键,两条链接(两个子节点),这种节点被称为2节点。2-3树中,引入了一个3节点的概念,它含有两个键,三条链接。左链接指向的键都小于该节点,中链接指向的键介于该节点的两个键之间,右链接指向的键都大于该节点。同理我们可以构造出4节点、5节点,在这样的树中,空节点到根节点的距离都是相同的,这样的树就是一棵平衡的2-3搜索树。
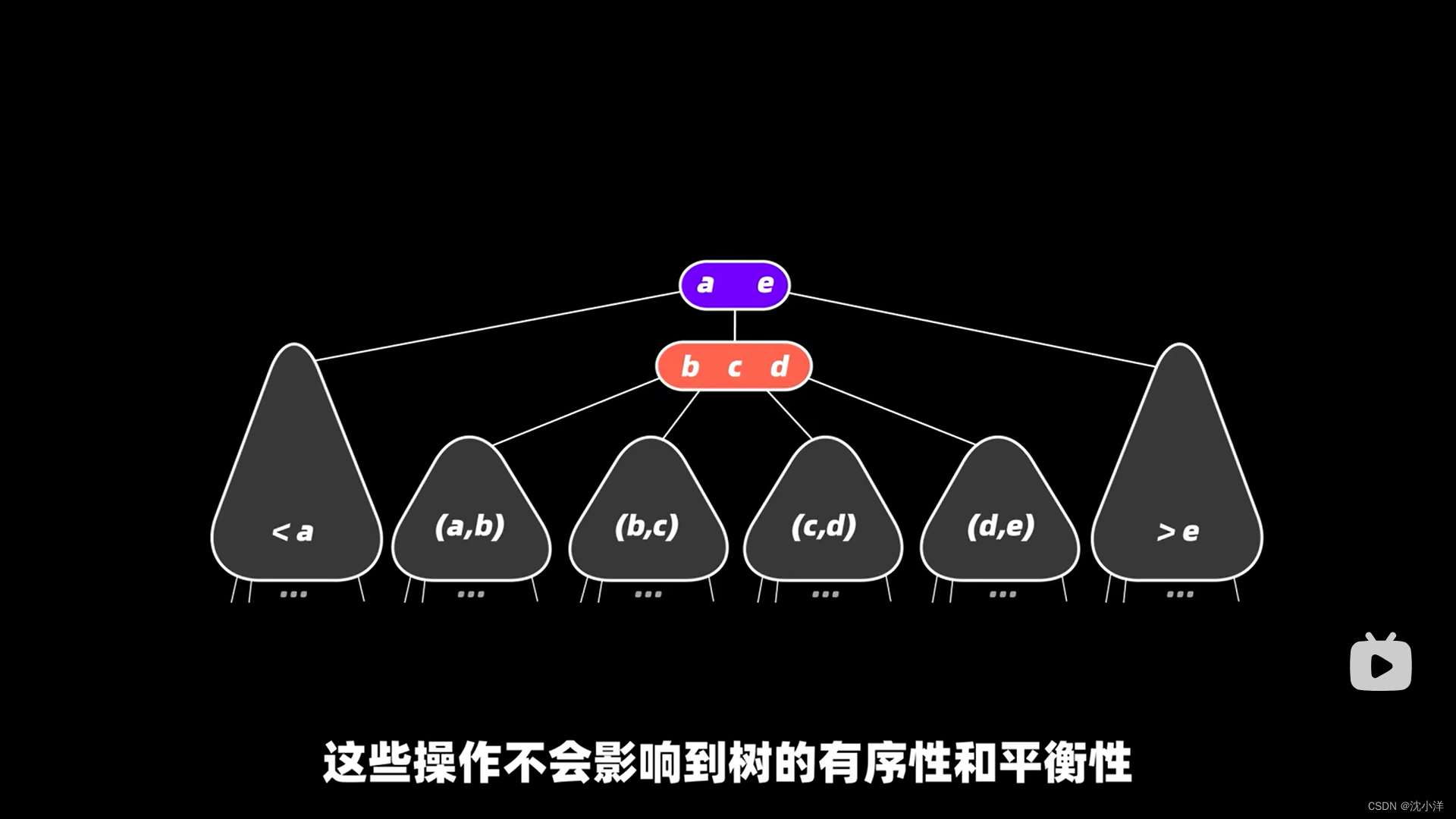
由于2-3树的新节点插入不是直接插入子节点,而是直接插入临近节点位置,然后判断是否需要拆分节点,拆分后向上合并节点,因此2-3树的生长方向是自底向上的,这也就保证了2-3树始终是平衡的。即使连续插入有序列表,生成出来的2-3树依然是高度平衡的。
节点的分解都在树的局部进行,因此分解操作不会影响树的平衡性和有序性。
2-3树实现的难点在于,它需要额外的数据类型来维护3节点,以及处理失衡的结构时,对不同类型的节点进行频繁的转换。
一种简化2-3树的思路
一种简化2-3树的思路是用2节点替换3节点,同时又能保持树的平衡性。
一棵标准2-3树
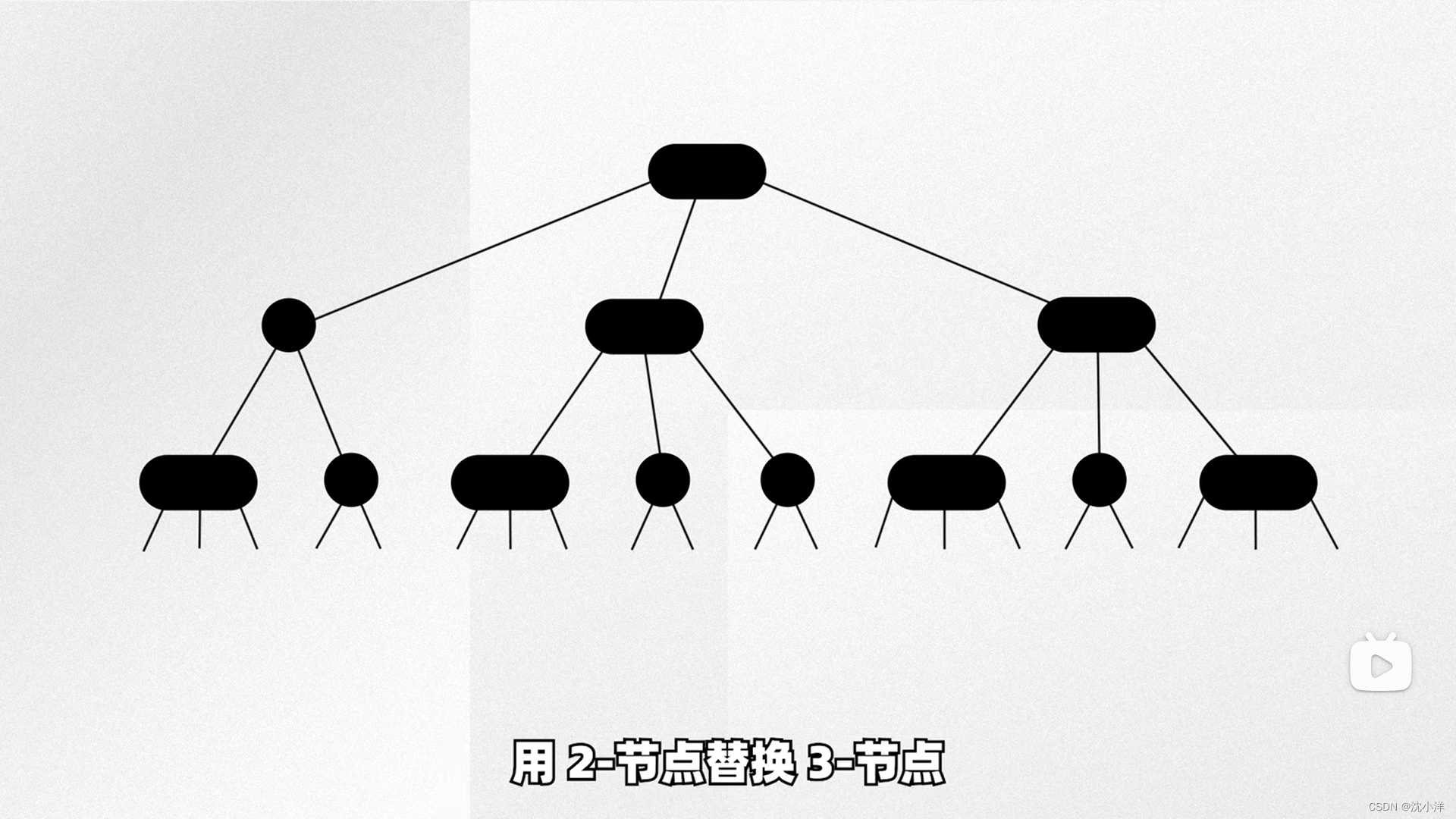
拆分3节点并标记左侧节点为红色
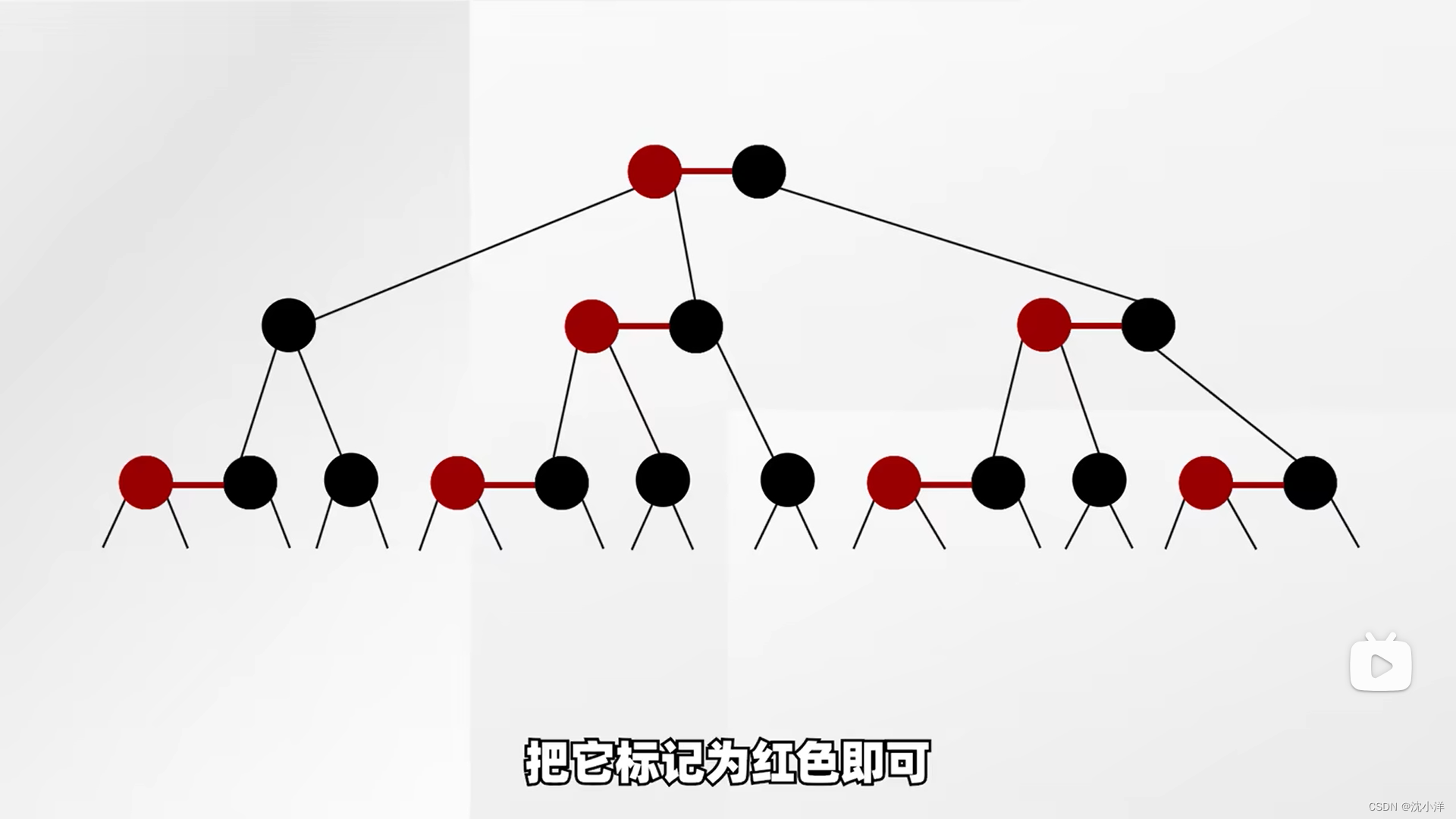
就得到了一棵红黑树(左倾红黑树)
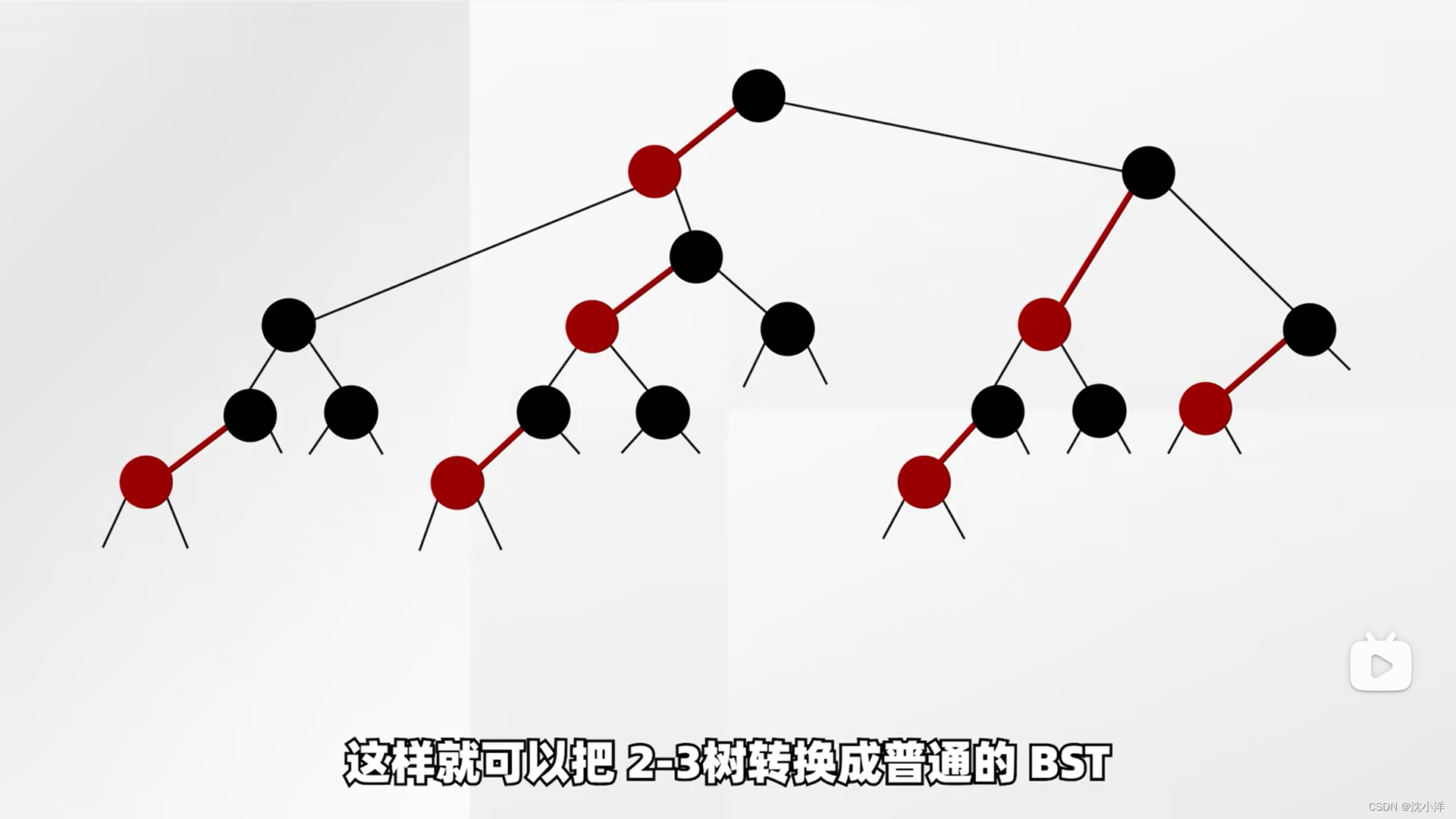
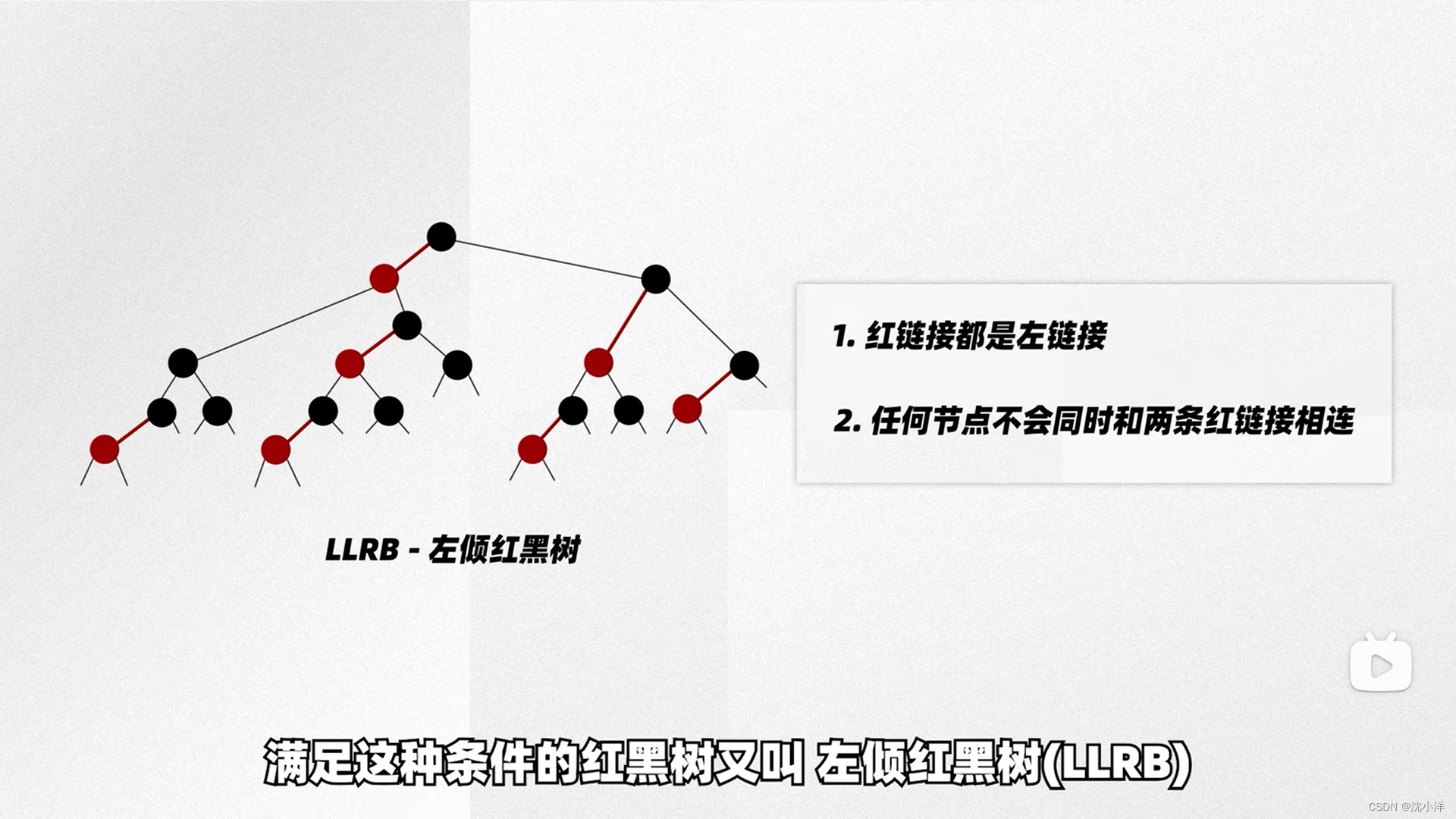
左倾红黑树
为了保证红黑树跟2-3树完全等价,我们需要以下定义:
- 红链接都是左链接
- 任何节点不会同时和2个红色节点相连
满足这2个条件的红黑树被称为左倾红黑树,它的实现相对标准红黑树更为简单。
红黑树的五条性质
- 节点是黑色或红色
- 根节点只能是黑色
- 所有叶子节点都是黑色(NIL)
- 不能出现连续的红色节点
- 任意节点到其每个叶子节点的每条路径都包含相同数量的黑色节点
若根节点为2节点,那其本身就是黑色节点,若根节点为3节点,那么黑色节点就是其中的较大元素,因此根节点总是黑色。
根据2-3树转化到红黑树的过程就可以很直观地看到,不会出现连续的红色节点,即使是基于2-3-4树实现的红黑树,4节点在红黑树中也是表现为一个黑色节点带两个红色子节点,因此一定不会出现连续的红色节点。
根据2-3树转化到红黑树的过程,可以看出红色节点总是依附黑色父节点而存在,因此在红黑树中只有黑色节点才真正贡献高度。2-3树本身具备高度平衡的特点,反映到红黑树中就是黑色节点完美平衡。
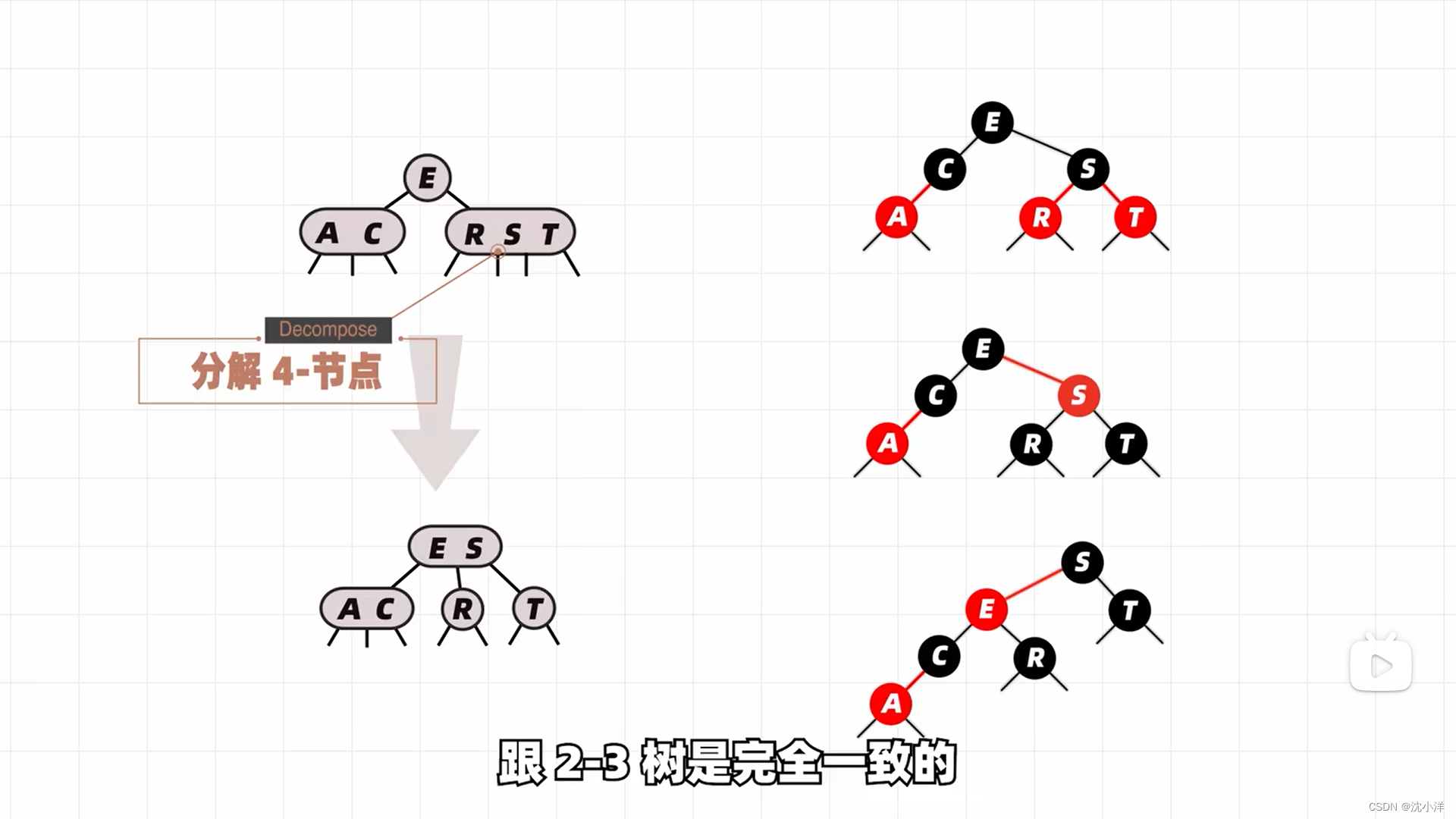
什么是4节点?
从结构上来看,简单理解,一个黑色节点带两个红色子节点就可以认为是一个4节点。下图是4节点分解的完整过程。
插入操作的3种情况
左倾红黑树的插入有三种可能的情况
情况1(出现左右两个红色子节点)
插入前黑父左边是红色节点,待插入节点比黑父大,插在了黑父的右边,此时出现右倾红节点。
注意,这种情况对应着2-3树中出现了临时4节点,我们在2-3树中的处理是将这个临时4节点分裂,左右元素各自形成一个2节点,中间元素上升到上层跟父节点结合。所以,我们在红黑树中的动作是,将原本红色的左右儿子染黑(左右分裂),将黑父染红(等待上升结合)。
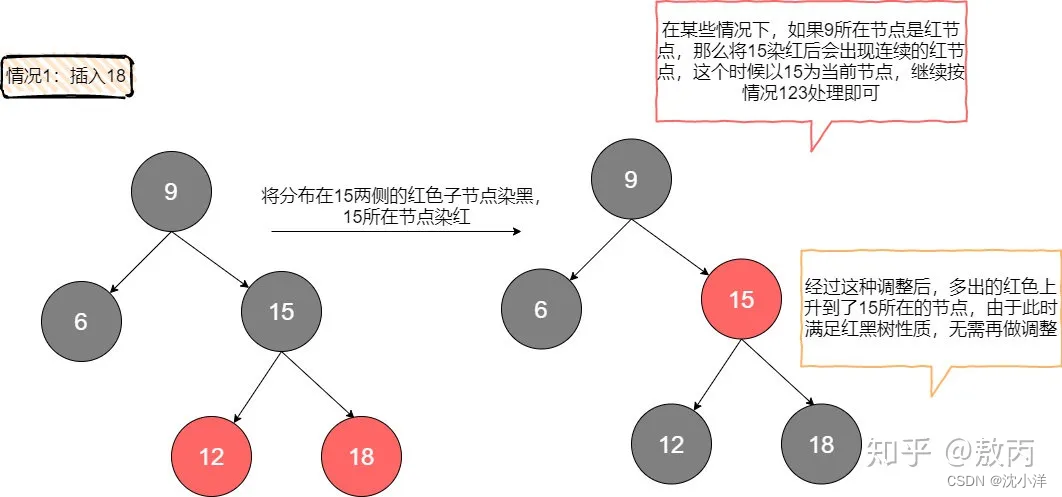
补充下特殊场景的处理,假设节点9也是红节点,那么就要先对节点9进行左旋,然后对左旋后的节点15的父节点(假设为节点X)进行右旋,并修改节点15为黑色,修改节点X为红色。然后我们就会发现又回到了场景一,之后继续按照情况1的规则继续处理即可。
情况2(左侧出现连续红色子节点)
待插入节点比红父小,且红父本身就是左倾红节点,也就是说,两个红节点靠在左边形成了连续的红节点。
这种情况我们需要用两步来调整。由于我们插入的是红色节点,其实不会破坏黑色完美平衡,所以要注意的是在旋转和染色的过程种继续保持这种完美黑色平衡。
首先对红父的父亲进行一次右旋,这次右旋不会破坏黑色平衡,但是也没有解决连续红色的问题。
接下来将12所在节点与15所在节点交换颜色,这样的目的是为了消除连续红色,并且这个操作依旧维持了黑色平衡。现在我们已经得到了情况1的场景,直接按情况1处理即可。

情况3(出现红色右节点)
待插入元素比红父大,且红父自身就是左倾。也就是说插入的这个节点形成了一个右倾的红色节点,对右倾的处理很简单,将红父进行一次左旋,就能使得右倾红节点变为左倾,现在出现了连续的左倾红节点,直接按情况2处理即可。
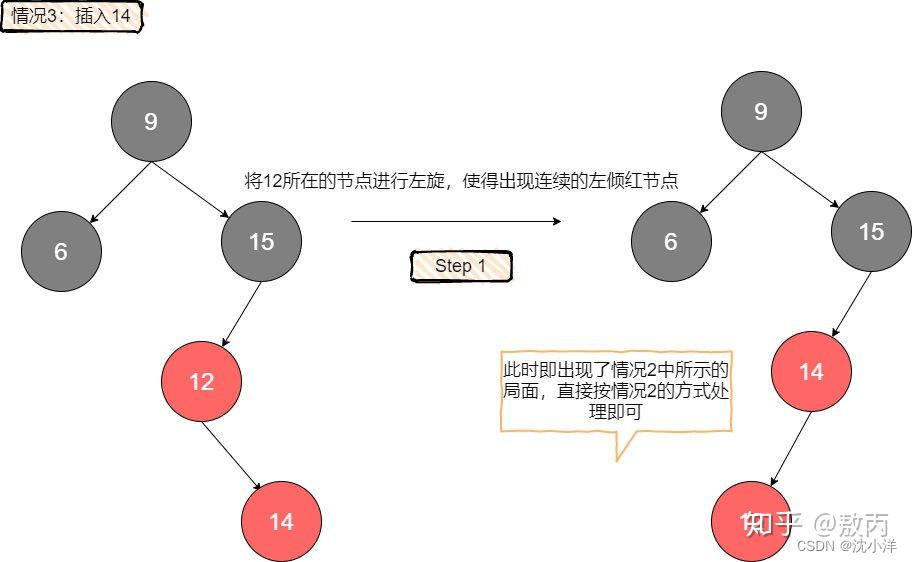
在插入时,可以体会到左倾红黑树对于左倾的限制带来的好处,因为在原树符合红黑树定义的情况下,如果父亲是红的,那么它一定左倾,同时也不用考虑可能存在的右倾兄弟(如果有,那说明原树不满足红黑树定义)。
这种限制消除了很多需要考虑的场景,让插入变得更加简单。
删除操作
删除节点要保证2点:不能破坏树的有序性、不能破坏树的平衡性。流程上可以分为2步,第一步向下递归,对红黑树进行预调整,删除目标节点。第二步向上回溯,修复预调整阶段被破坏的红黑树。
如果要删除的节点是红黑树中的中间节点,那么删除节点后树的调整会非常复杂,因为要同时考虑父节点与子节点的情况。有一种简单的方法是,需要删除某个节点时,不直接删除该节点,而是改为删除它的前驱或后继节点,把删除节点的值直接赋值给当前要删除的节点。假设改为删除它的后继节点,那么情况就可以简化为删除叶子节点或者只包含一个子节点的节点,这可以大大简化后续需要执行的操作。
向下递归
我们从根节点出发,基于2-3树的预合并策略对红黑树进行调整。具体的做法是,每次都保证当前的节点是2-3树中的非2节点,如果当前节点已经是非2节点,那么直接跳过;如果当前节点是2节点,那么根据兄弟节点的状况来进行调整:
- 如果兄弟是2节点,那么从父节点借一个元素给当前节点,然后与兄弟节点一起形成一个临时4节点。
- 如果兄弟是非2节点,那么兄弟上升一个元素到父节点,同时父节点下降一个元素到当前节点,使得当前节点成为一个3节点。
这样的策略能够保证最后走到待删除节点的时候,它一定是一个非2节点,我们可以直接将其元素删除。
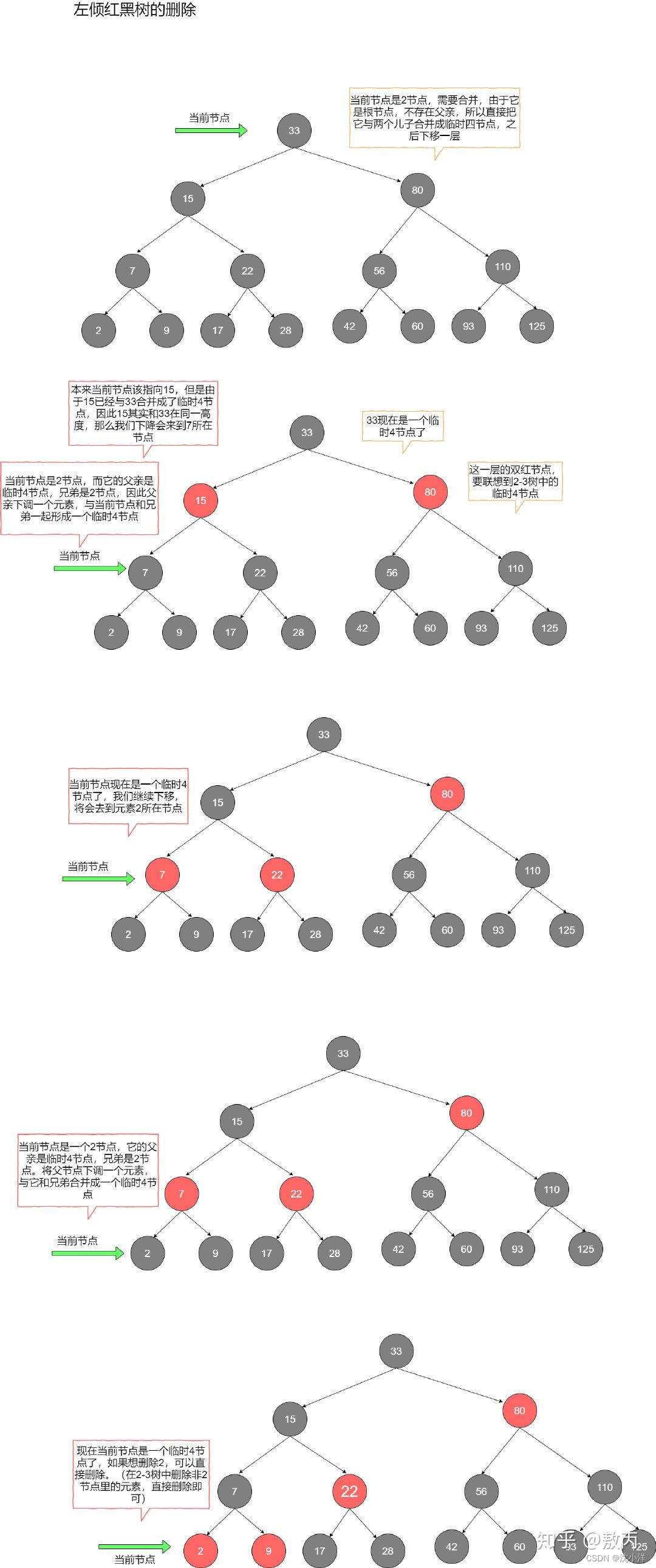
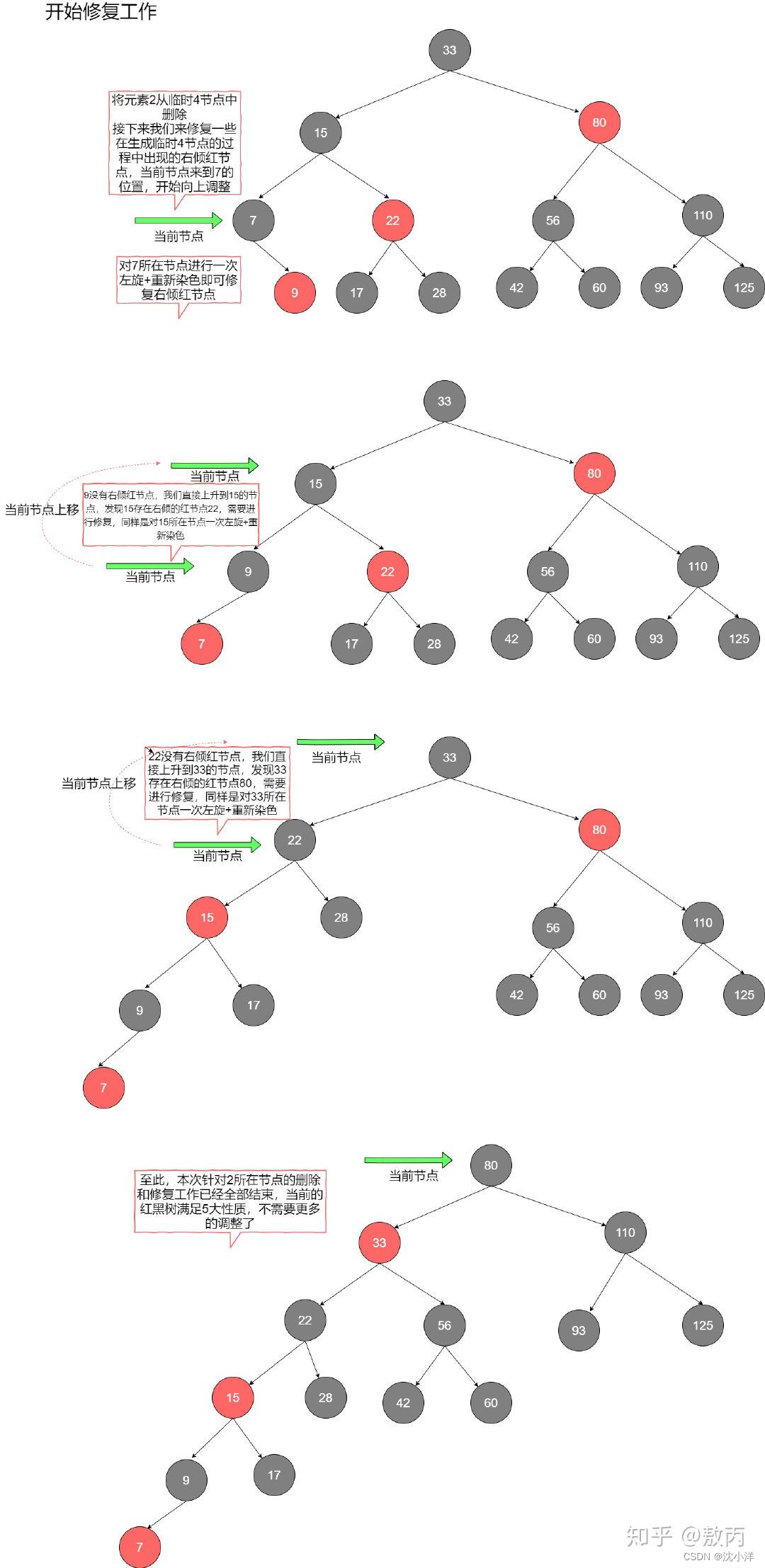
向上回溯
接下来要考虑的是修复工作,由于红黑树定义的限制,我们在调整的过程中出现了一些本不该存在的红色右倾节点(因为生成了概念模型中的临时4节点),于是我们顺着搜索的方向向上回溯,如果遇到当前节点具备右倾的红色儿子,那么对当前节点进行一次左旋,这时原本的右儿子会来到当前节点的位置,然后将右儿子与当前节点交换颜色,我们就将右倾红节点修复成了左倾红节点,同时我们并没有破坏黑色节点的平衡。
记录哪些笔记?能够让人很久以后依然能够比较容易看懂?
- 红黑树实际上是2-3树的一种实现
- 介绍红黑树的5条定义
- 能不能不介绍左旋右旋?
- 介绍下什么是『临时4节点』
- 直接写插入和删除的场景?
2-3-4树 -> 标准红黑树
为什么不直接实现2-3树或者2-3-4树?
因为直接实现太过复杂,需要处理不同节点间的转换,分解4节点和5节点需要处理的情况太多,需要考虑4节点的位置情况,需要考虑父节点是2节点还是3节点,4节点是左节点、右节点还是中间节点等等,而且实现后需要大量额外的开销,实际性能并不理想,因此实际应用很少。
参考链接
红黑树-维基百科
红黑树_百度百科
《算法》(第4版) - chapter 3.3 红黑树_哔哩哔哩_bilibili
图解:什么是红黑树? - 知乎




![[动画+注释详解]数据结构 - 直接插入排序](https://img-blog.csdnimg.cn/direct/0ba72997cd4248d7b6bb6f4accc237e6.png)