力扣题目链接

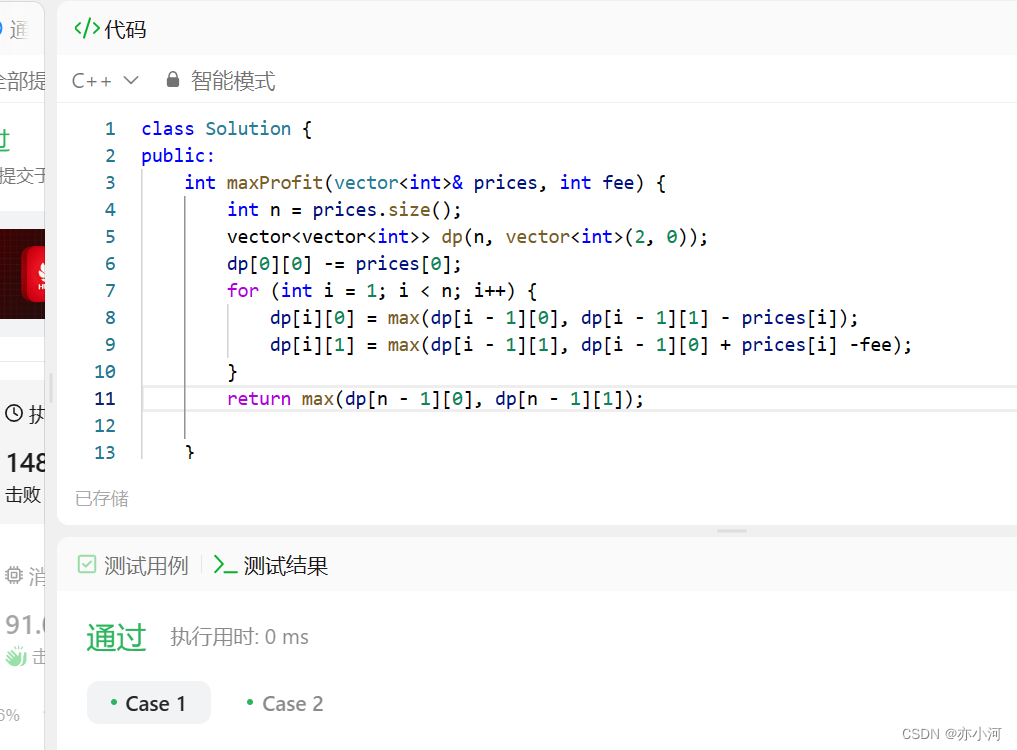
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2, 0));
        dp[0][0] -= prices[0]; // 持股票
        for (int i = 1; i < n; i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return max(dp[n - 1][0], dp[n - 1][1]);
    }
};

思路

本题贪心解法：贪心算法：买卖股票的最佳时机含手续费(opens new window)

性能是：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

本题使用贪心算法并不好理解，也很容易出错，那么我们再来看看是使用动规的方法如何解题。

相对于动态规划：122.买卖股票的最佳时机II (opens new window)，本题只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的。

唯一差别在于递推公式部分，所以本篇也就不按照动规五部曲详细讲解了，主要讲解一下递推公式部分。

这里重申一下dp数组的含义：

dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来

• 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
• 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

所以：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

在来看看如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来

• 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
• 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i - 1][0] + prices[i] - fee

所以：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);

本题和动态规划：122.买卖股票的最佳时机II (opens new window)的区别就是这里需要多一个减去手续费的操作。

代码随想录 (programmercarl.com)