【多维动态规划】Leetcode 62. 不同路径【中等】

news2024/12/29 9:33:01

不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

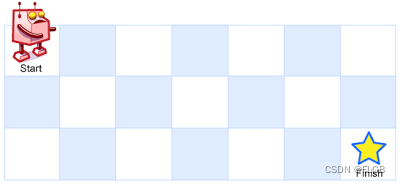
在这里插入图片描述

输入：m = 3, n = 7
输出：28

解题思路

1、由于机器人每次只能向下或向右移动一步，那么到达网格右下角的路径就是从起点出发，
经过若干次向右和向下的移动后到达终点的路径。
2、可以使用动态规划来解决，定义一个二维数组 dp，其中 dp[i][j] 表示从起点到达网格第 i 行第 j 列位置的路径数量。
3、对于网格中的任意一个位置 (i, j)，到达该位置的路径数量等于其上方格子和左侧格子路径数量之和，即 dp[i][j] = dp[i-1][j] + dp[i][j-1]。
4、起点位置的路径数量为 1，第一行第一列也是1，因为只有一条路径可以到达。

Java实现

public class UniquePaths {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];

        // 初始化起点位置的路径数量为1
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }

        // 计算每个位置的路径数量
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        // 返回终点的路径数量
        return dp[m-1][n-1];
    }

    public static void main(String[] args) {
        UniquePaths solution = new UniquePaths();
        int m = 3, n = 7;
        System.out.println("Total number of unique paths: " + solution.uniquePaths(m, n)); // Output: 28
    }
}