本文字数:3151字
预计阅读时间:20分钟
![]()
在现代设计中,动效图在APP的UI界面中所起到的作用无疑是显著的。相比于静态的界面,动效更符合人类的自然认知体系,它有效地降低了用户的认知负载,UI动效俨然已经成为了不可或缺的一部分。
那么在开发过程中,当遇到UI提供的动态物料满足不了内存以及效果的要求时,我们程序员就不得不通过代码自己去实现效果,这就引出了我们今天要实现的这个旋转变色圆角三角形。当时接到需求的时候,我也以为只要UI同学提供物料即可,但是实验的时候发现如果想呈现动效效果好一点的话,在不同的手机上可能会发生丢帧,OOM以及图形的严重锯齿化等一系列问题,最后实现这个效果的重任就落到了我们程序员的头上(很头大)。
记得当时为了实现这个动画效果,也是发挥了我尘封已久的初中数学知识,还有朋友的帮忙,才能顺利完成开发任务。所以虽然时间过去了很久,依然想做个记录,供大家参考探讨!废话说完终于要进入正题了,大家可以看一下这个UI动效,见下图:

首先我们仔细看这个动画,将它进行静态化拆分,大概如下图:

其实它的组成还是相对简单的,就是由以下这几个元素构成:黑色的三角形,沿着黑色三角形运动的红色/黑色轨迹,还有整体的旋转。那么我们就按部就班地一步一步来就行了。
第一步:画出一个“被放倒”的等边黑色三角形
问题来了,它三个角的坐标怎么确定呢?这里我们可以先考虑一下,它是要旋转的,等边三角形旋转的轨迹肯定是一个圆,那么呼之欲出的,到这里就需要我们拿出初中的数学知识了——三角形的外接圆,通过它,我们就能够确认出这个三角形的坐标系,也就是三个顶点的坐标位置,自然就可以连线出这个三角形的形状,具体做法如下:
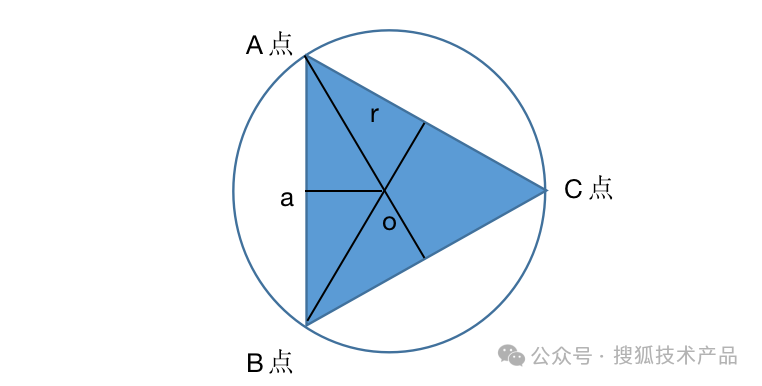
通过上面这个图,相信能唤醒一些数学基本知识了。我们以o点为坐标系的原点,边长我们命名为a,外接圆半径是r,那么:
A点的x坐标就应该是负的外接圆半径除以2,y坐标是负的三角形的边长除以2,即(-r/2,-a/2);
B点的x坐标应该是负的外接圆半径/2, y坐标是三角形的边长除以2,即(-r/2,a/2);
C点的x坐标应该是外接圆半径,y坐标是0,即(r,0)。
在这个过程中又一个问题出现了,外周圆的半径怎么确认呢?数学公式已经忘得差不多了,但是百度出真知,果然,度娘给出了我们想要的答案:r=√3/3*a,所以我们现在就可以确认这三个点的坐标值了这个过程转换成代码我们就实现了第一步了,具体代码如下:
1、自定义一个View,然后定义出我们所需要的这些变量:
private Paint mPaint; //画笔
private Path mPath; //三个点连成线的路径2、确定这个view的大小,我们可以暂定设置为100dp(当然这个是可以xml动态设置的):
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
setMeasuredDimension(getDefaultSize(0, widthMeasureSpec), getDefaultSize(0, heightMeasureSpec));
int childHeightSize = DisplayUtils.dipToPx(getContext(), 100);
heightMeasureSpec = MeasureSpec.makeMeasureSpec(childHeightSize, MeasureSpec.EXACTLY);
int childHeightWidth = DisplayUtils.dipToPx(getContext(), 100);
widthMeasureSpec = MeasureSpec.makeMeasureSpec(childHeightWidth, MeasureSpec.EXACTLY);
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
}3、在初始化的时候,我们按照上面分析的数学步骤先初始化它的坐标系:
private void initCoordinate() {
x0 = -(float) (Math.sqrt(3) * mWidth / 6);
y0 = -mWidth / 2;
x1 = (float) (Math.sqrt(3) * mWidth / 3);
y1 = 0;
x2 = -(float) (Math.sqrt(3) * mWidth / 6);
y2 = mWidth / 2;
}4、我们初始化它的画笔,注意我们这个三角形的拐角部分都是圆角,所以需要特别设置一下:
private void initPaint() {
mPaint = new Paint();
mPaint.setAntiAlias(true);//抗锯齿
mPaint.setStyle(Paint.Style.STROKE);//画线模式 mPaint.setStrokeWidth(DisplayUtils.dipToPx(mContext, 2));
//设置所有拐角处变成圆角
mPaint.setPathEffect(new CornerPathEffect(10));
mColorBlack = mContext.getResources().getColor(R.color.bg_333333);
mPaint.setColor(mColorBlack);
}5、将三点连线:
private void initPath() {
mPath = new Path();
mPath.moveTo(x0, y0);
mPath.lineTo(x1, y1);
mPath.lineTo(x2, y2);
mPath.close();
}6、在onDraw方法中 把坐标中心挪到画布的中心 然后把他们画出来:
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//移动坐标系
canvas.translate(getMeasuredWidth() / 2, getMeasuredHeight() / 2);
canvas.drawPath(mPath, mPaint);
}到这一步 我们run一下代码,果然整个静态黑色圆角三角形 就可以呈现出来了,如下图:

第二步:进行红/黑线走向的绘制
仔细观察可以得出,红/黑线是onebyone,在等同的时间内,走完这个静态三角形轨迹的,属性动画应该可以搞定,动画不难,难的是利用进度进行计算的这个过程,我们下面主要说说获取到动画进度后,怎么计算红/黑线的坐标数值。
首先,我们要定义一个动态的点(x,y)用来记录红/黑线这个走向的坐标点,接下来,我们就要根据这个黑色三角形的三个顶点,通过属性动画计算(x,y)的路径,步骤如下:
1、我们确定画笔的起点以及终点也就是三个顶点,如第一段的起点就是(x0,y0)终点就是(x1,y1),第二段的起点就是(x1,y1)终点就是(x2,y2)以此类推第三个点的坐标也很容易确认;
2、因为是等边三角形,所以这个边的动画进度应该是总进度的三分之一,第一段应该就是0至1/3 第二段就是1/3至1/32 , 第三段就是1/32至1;
3、利用path.lineTo进行两点的连接以上几步转换成代码如下所示:
if (progress < 0.33333333f) { //第一段
float progressInLine = progress / 0.33333333f;
path.lineTo(x + Math.abs(x1 - x) * progressInLine, y + Math.abs(y1 - y) * progressInLine);
} else if (progress < 0.66666666f) {//第二段
float progressInLine = (progress - 0.33333333f) / 0.33333333f;
path.lineTo(x1, y1);
path.lineTo(x1 - Math.abs(x2 - x1) * progressInLine, y1 + Math.abs(y2 - y1) * progressInLine);
} else if (progress < 1) {//第三段
float progressInLine = (progress - 0.66666666f) / 0.33333333f;
path.lineTo(x1, y1);
path.lineTo(x2, y2);
path.lineTo(x2, y2 - Math.abs(y2 - y0) * progressInLine);
} else if (progress >= 1f) {
path.lineTo(x1, y1);
path.lineTo(x2, y2);
path.lineTo(x0, y0);
path.close();
}但是,这样计算之后,你会发现,这个动画是有瑕疵的,见下图:

就是在画线的时候,你会发现在角的地方会突出去一点,这是为什么呢?还记得咱们之前设置过一个圆弧半径10吗,就是这个小小的弧度导致了我们要连接坐标的实际距离其实是缩短了的,具体可以观察以下两个图(弧度弄得有点夸张,这样比较明显):

很明显两个三角形的边长是不一样的,所以,我们不能单纯的只是连接这个三角形的顶点,还需要计算出圆弧导致的偏移量,这时候又要搬出三角函数了,已知圆弧半径,我们可以利用余弦和正弦分别求出x和y的偏移值(具体公式可以百度),代码如下:
float offsetX= (float) (10* Math.sin(Math.PI * 60 / 180));
float offsetY = (float) (10* Math.cos(Math.PI * 60 / 180));那么刚才的代码步骤就会变成:
if (progress < 0.33333333f) { //第一段
float fromX1 = x1 - offsetX;
float fromY1 = y1 - offsetY;
float progressInLine = progress / 0.33333333f;
path.lineTo(x + Math.abs(fromX1 - x) * progressInLine, y + Math.abs(fromY1 - y) * progressInLine);
} else if (progress < 0.66666666f) {//第二段
float progressInLine = (progress - 0.33333333f) / 0.33333333f;
float fromX1 = x1 - offsetX;
float fromY1 = y1 + offsetY;
float desX2 = x2 + offsetX;
float desY2 = y2 - offsetY;
path.lineTo(x1, y1);
path.lineTo(fromX1 - Math.abs(desX2 - fromX1) * progressInLine, fromY1 + Math.abs(desY2 - fromY1) * progressInLine);
} else if (progress <1) {//第三段
float progressInLine = (progress - 0.66666666f) / 0.33333333f;
float fromY2 = y2 - offsetY;
float desY0 = y0 + offsetY;
path.lineTo(x1, y1);
path.lineTo(x2, y2);
path.lineTo(x2, fromY2 - Math.abs(fromY2 - desY0) * progressInLine);
} else if (progress >= 1f) {
......
}第三步:在黑色走线时使三角形转起来
首先我们要确认旋转的角度,由于等边三角形的三个角完全相同,旋转时,只要使下一个角对准原角,就能重合,所以一圈360度除以3,就得到120度.也就是说旋转120度就可以跟原三角形完全重合,但是我们的效果是 a角转到b角 所以 我们直接除以3 也就是旋转40度即可到达我们的预想效果了,转换成代码如下:
private void computePath(float progress) {
float progressInRotate = progress;
mDegree = 40 * progressInRotate;//黑线旋转使用
......
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//移动坐标系
canvas.translate(getMeasuredWidth() / 2, getMeasuredHeight() / 2);
//旋转 注意顺序
canvas.rotate(mDegree);
canvas.drawPath(mPath, mPaint);
}到此 这个旋转变色的圆角三角形就绘制完成了,虽然效果看上去比较简单,但是实际开发起来还是有一些细节需要注意的,仅此给大家提供一个实现类似效果的小思路,也希望大家可以在评论区提出自己更好的想法,如果需要源码,可以联系我~



![[每周一更]-(第94期):认识英伟达显卡](https://img-blog.csdnimg.cn/direct/55778f93225c49e19100205642d2d51d.jpeg#pic_center)


![Amazon云计算AWS之[5]关系数据库服务RDS](https://img-blog.csdnimg.cn/direct/c7e33d19d32141df9eeb3f9714c4bd2e.png)