数据结构——二叉树的顺序存储(堆)(C++实现)
- 二叉树可以顺序存储的前提
- 堆的定义
- 堆的分类
- 大根堆
- 小根堆
- 整体结构把握
- 两种调整算法
- 向上调整算法
- 递归版本
- 非递归版本
- 向下调整算法
- 非递归版本
- 向上调整算法和向下调整算法的比较
我们接着来看二叉树:
二叉树可以顺序存储的前提
完全二叉树完全符合顺序存储的前提:
完全二叉树:顺序存储二叉树最适合应用于完全二叉树。完全二叉树是一种特殊的二叉树,除最后一层外,每一层都被完全填满,并且所有结点尽可能集中在左边。由于其结构特性,完全二叉树的结点与数组下标之间存在着直接的数学映射关系,**使得每个结点可以按照固定规则(如左孩子为2i,右孩子为2i+1)**在数组中找到其相应的位置。这种映射保证了数组的存储空间得以充分利用,没有浪费。
顺序存储的二叉树我们称为堆:
堆的定义
堆是一种特殊的树形数据结构,通常以数组的形式进行顺序存储。堆具有以下关键性质:
-
完全二叉树结构:
堆是一个完全二叉树或近乎完全二叉树。这意味着除了可能的最后一层外,其他各层都是完全填充的,并且最后一层的所有结点都尽可能靠左排列。这种结构非常适合用数组来表示,因为完全二叉树的结点与数组下标之间存在直接的数学映射关系,使得每个结点可以高效地通过下标访问。 -
堆序性质:
堆分为两种主要类型:最大堆和最小堆。无论哪种类型,堆都遵循特定的堆序性质:
- 大根堆:每个结点的值都大于或等于其子结点的值。即对于任意结点 i,其值
A[i]大于等于其左孩子A[2*i+1]和右孩子A[2*i+2]的值。- 小根堆:每个结点的值都小于或等于其子结点的值。即对于任意结点 i,其值
A[i]小于等于其左孩子A[2*i+1]和右孩子A[2*i+2]的值。
由于堆的完全二叉树特性和堆序性质,它非常适合使用数组进行顺序存储。具体来说:
- 数组下标与结点关系:
假设数组
A存储了一个堆,根结点位于下标0。那么对于任一结点 i,其左孩子、右孩子的下标分别为2*i + 1和2*i + 2,而其父结点的下标为(i - 1) // 2(向下取整)。这种固定的下标关系使得在数组中进行堆的操作(如插入、删除、调整等)变得非常直观和高效。
- 空间利用率:
由于堆是完全或近乎完全二叉树,其存储在数组中时空间利用率较高。即使不是严格的完全二叉树,只要整体结构相对平衡,数组中的空闲位置也相对较少,不会造成过多的存储浪费。
- 操作复杂度:
堆的常见操作(如插入、删除堆顶元素、调整堆等)的时间复杂度通常为 O(log n),这是因为堆的高度与结点数成对数关系。数组的随机访问特性使得这些操作能够在常数时间内定位到相关结点,然后通过递归或迭代方式进行堆结构调整。
因此,堆作为一类满足特定条件的二叉树,其完全二叉树特性、堆序性质以及高效的操作性能,使其非常适合采用数组进行顺序存储。堆常用于实现优先队列、求解Top-K问题、堆排序算法等场景。
堆的分类
大根堆
大根堆是一种特殊的二叉堆,其中每个节点的值都大于或等于其子节点的值。具体地说,对于大根堆中的任意节点
i,其值 A[i] 大于等于其左孩子A[2*i+1]和右孩子A[2*i+2]的值。根节点(数组下标为1或0,取决于实现)总是包含堆中的最大值。大根堆常用于实现优先队列,其中队首元素始终为当前最大的元素。
小根堆
小根堆也是一种特殊的二叉堆,其中每个节点的值都小于或等于其子节点的值。对于小根堆中的任意节点 i,其值
A[i]小于等于其左孩子A[2*i+1]和右孩子A[2*i+2]的值。根节点(同样为数组下标为1或0)始终包含堆中的最小值。小根堆同样适用于优先队列的场景,但此时队首元素为当前最小的元素。
整体结构把握
我们这里用vector作为底层容器来存储数据,这些数据按照顺序排放:
#pragma once
#include<iostream>
#include<vector>
template<class T>
//堆的定义
class Heap
{
public:
Heap()
:_size(0)
{
_data.resize(10);
}
Heap(const size_t& size)
:_size(0)
{
_data.resize(size + 1);
}
//插入
void insert(const T& data)
{
if(_size > _data.capacity())
{
_data.resize(2 * _data.size());
}
_data[++_size] = data;
}
//是否为空
bool empty()
{
return _size == 0;
}
//打印堆
void printHeap()
{
for(int i = 1; i < _size + 1; i++)
{
std::cout<< _data[i] << " ";
}
std::cout << std::endl;
}
private:
std::vector<T> _data; //存放数据
size_t _size; //当前数据个数
};
这里注意一下,我的一个数据并没有放在0号位置,而是放在了1号位置,这样方便我们寻找父节点:
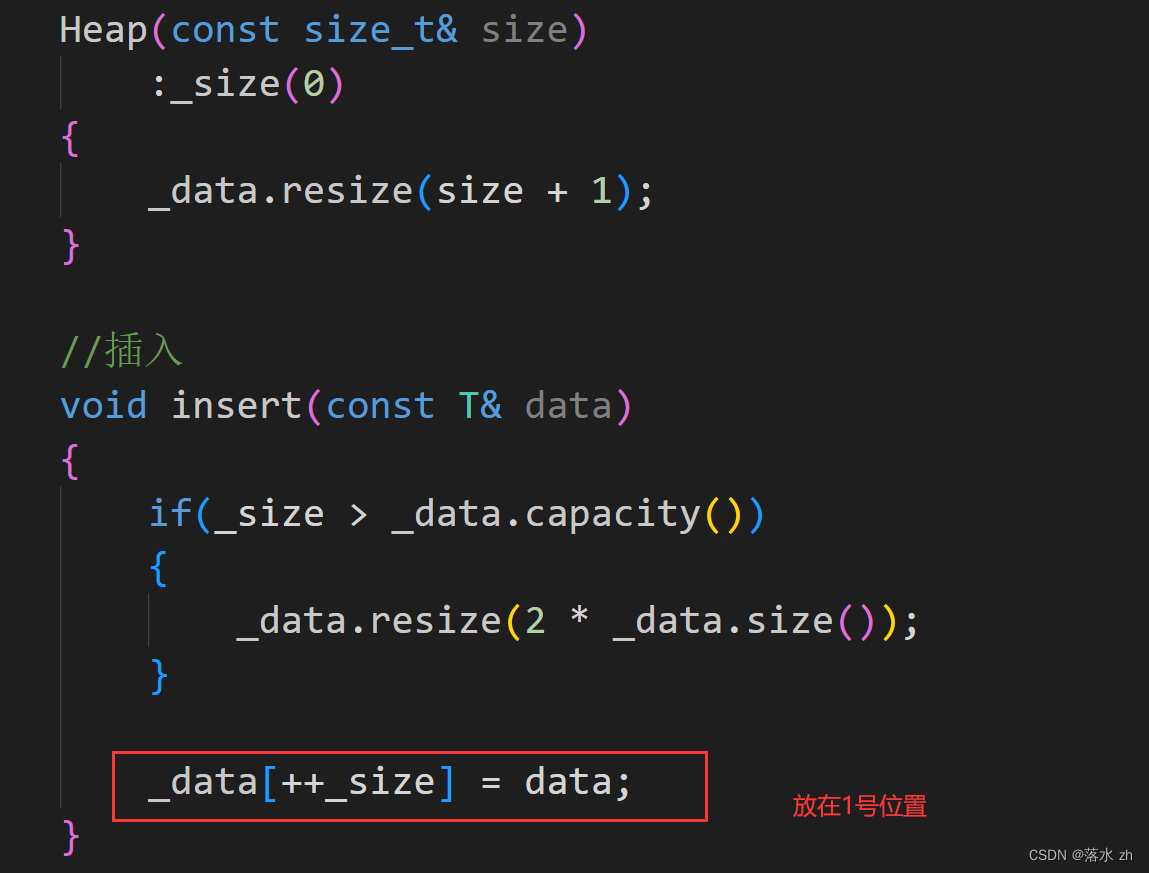
我们可以先测试一下:
#include"heap.h"
int main()
{
Heap<int> heap;
heap.insert(12);
heap.insert(23);
heap.insert(1);
heap.insert(0);
heap.insert(24);
heap.insert(4);
heap.insert(188);
heap.insert(9);
heap.insert(58);
heap.printHeap();
return 0;
}
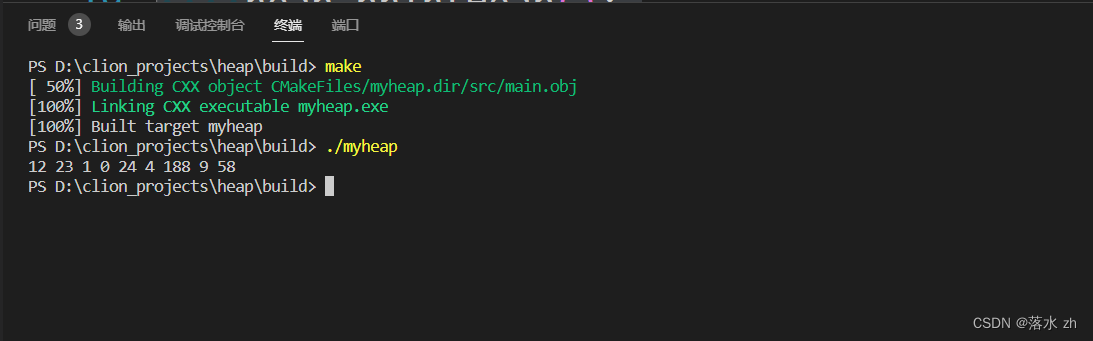
两种调整算法
向上调整算法
向上调整算法的核心是把每一个结点都当做孩子,去跟自己的父亲比较,如果比自己的父亲大(或者小)交交换数据:
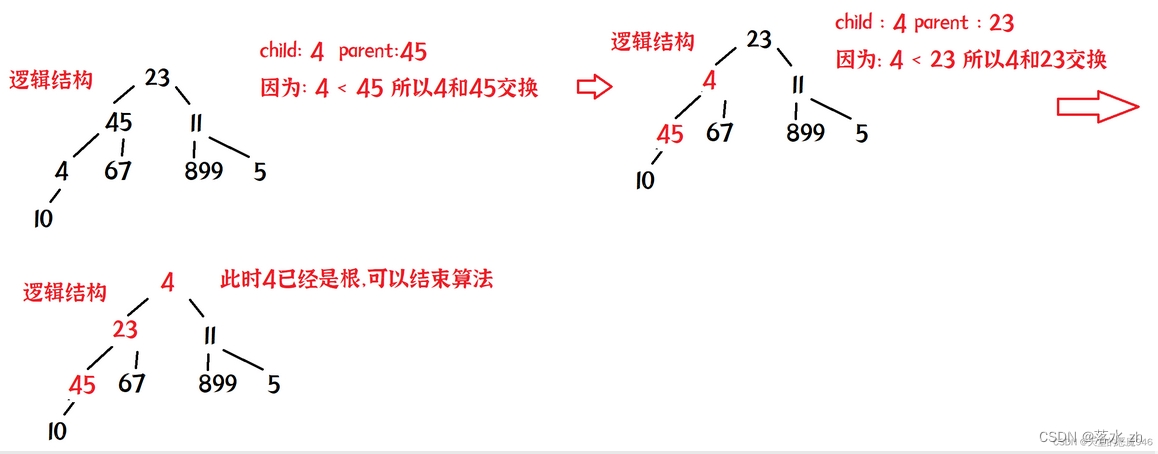
递归版本
递归版本比较好想,我只管我自己和父亲的比较,比较完之后,继续向上比较:
// 向上调整函数(以小根堆为例)
// 输入参数:index - 需要进行调整的子节点索引
void sifUpHeap(const size_t& index)
{
// 如果索引小于 1,说明已经到达根节点或无效索引,无需继续调整,直接返回
if (index < 1)
{
return;
}
// 获取当前子节点的父节点索引
size_t parentIndex = Parent(index);
// 如果子节点索引大于 1(即不是根节点),并且子节点的值小于其父节点的值
// 则交换两者,确保父节点的值小于其子节点的值(小根堆性质)
if (index > 1 && _data[parentIndex] > _data[index])
{
std::swap(_data[parentIndex], _data[index]);
// 对交换后的新父节点(原子节点)继续进行向上调整,确保整棵子树满足小根堆性质
sifUpHeap(parentIndex);
}
// 返回,完成当前节点的向上调整过程
return;
}
但是我们这样只是完成了一个数据的调整,我们要所有的数据进行调整:
//向上调整算法(以小根堆为例)
void sifUpHeap(const size_t& index)
{
if (index < 1)
{
return;
}
if(index > 1 && _data[Parent(index)] > _data[index])
{
std::swap(_data[Parent(index)],_data[index]);
//接着向上
sifUpHeap(Parent(index));
}
return;
}
//调整为小根堆
void ToMinHeap()
{
for(int i = 1; i < _size + 1; i++)
{
sifUpHeap(i);
}
}

非递归版本
我们也可以不用递归,使用迭代来完成:
// 向上调整函数(非递归版本,以小根堆为例)
// 输入参数:child - 需要进行调整的子节点索引
void sifUpHeap_non(size_t child)
{
// 计算当前子节点的父节点索引
size_t parent = child / 2;
// 循环迭代,直到子节点成为根节点或已满足小根堆性质
while (child > 1)
{
// 如果子节点的值小于其父节点的值
// 则交换两者,确保父节点的值小于其子节点的值(小根堆性质)
if (_data[Parent(child)] > _data[child])
{
std::swap(_data[Parent(child)], _data[child]);
// 更新子节点索引为交换后的父节点索引,准备对新的子节点进行下一轮比较
child = parent;
// 重新计算父节点索引
parent = child / 2;
}
else
{
// 子节点已满足小根堆性质,跳出循环,结束调整
break;
}
}
}
//调整为小根堆
void ToMinHeap()
{
for(int i = 1; i < _size + 1; i++)
{
sifUpHeap_non(i);
}
}
向下调整算法
向下调整算法是把所有结点当做父亲结点,去和自己的孩子结点比较,看哪个孩子结点比自己大或小,就交换:
 向下调整算法有个条件:左右子树必须为堆,因为这个特性,我们向下调整算法得从最后一个有孩子的双亲结点开始:
向下调整算法有个条件:左右子树必须为堆,因为这个特性,我们向下调整算法得从最后一个有孩子的双亲结点开始:
// 下降调整函数(以小根堆为例)
// 输入参数:index - 需要进行调整的父节点索引
void sifDownHeap(const size_t& index)
{
// 计算当前父节点的左孩子索引
size_t leftchild = LeftChild(index);
// 如果左孩子索引超出了堆的有效范围(即不存在左孩子),说明无需调整,直接返回
if (leftchild > _size)
{
return; // 超出范围,无需调整
}
// 初始化 "miner" 为当前父节点的左孩子索引
// "miner" 用于记录待调整子节点中值最小的那个的索引
int miner = leftchild;
// 比较左孩子与右孩子(如果存在)的值,确定哪个子节点的值更小
// 如果右孩子存在且其值小于左孩子,更新 "miner" 为右孩子索引
if (index < _size + 1 && _data[leftchild] > _data[leftchild + 1])
{
miner++;
}
// 如果当前父节点的值大于其最小子节点(即 "miner" 所指向的子节点)的值
// 则交换两者,确保父节点的值小于其子节点的值(小根堆性质)
if (_data[miner] < _data[index])
{
std::swap(_data[miner], _data[index]);
// 对交换后的新父节点(原子节点)继续进行向下调整,确保整棵子树满足小根堆性质
sifDownHeap(miner);
}
// 返回,完成当前节点的向下调整过程
return;
}
//调整为小根堆
void ToMinHeap()
{
// for(int i = 1; i < _size + 1; i++)
// {
// sifUpHeap_non(i);
// }
for(int i = _size / 2 ; i >=1 ; i--) //从最后一个父节点结点开始调整
{
sifDownHeap(i);
}
}
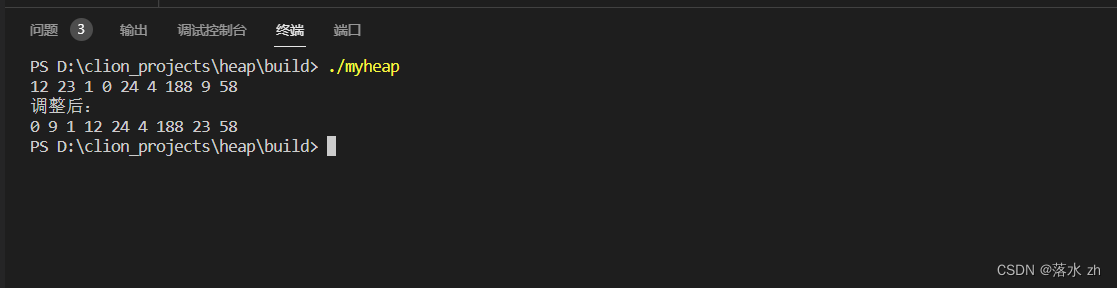
非递归版本
我们也可以用非递归的方式实现:
// 下降调整函数(以小根堆为例)
// 输入参数:parent - 需要进行调整的父节点索引
void sifDownHeap_non(size_t parent)
{
// 计算当前父节点的左孩子索引,假定左孩子为待调整子节点中值最小的一个
int child = LeftChild(parent);
// 循环迭代,直到越界
while (child < _size + 1)
{
// 如果右孩子存在且其值小于左孩子,更新 "child" 为右孩子索引
// 保持 "child" 指向待调整子节点中值最小的那个
if (parent + 1 < _size + 1 && _data[child] > _data[child + 1])
{
child++;
}
// 如果当前父节点的值大于其最小子节点(即 "child" 所指向的子节点)的值
// 则交换两者,确保父节点的值小于其子节点的值(小根堆性质)
if (_data[parent] > _data[child])
{
std::swap(_data[parent], _data[child]);
// 更新父节点索引为交换后的子节点索引,准备对新的子节点进行下一轮比较
parent = child;
// 重新计算子节点索引,从新的父节点开始
child = LeftChild(parent);
}
else
{
// 子节点已满足小根堆性质,跳出循环,结束调整
break;
}
}
}
//调整为小根堆
void ToMinHeap()
{
// for(int i = 1; i < _size + 1; i++)
// {
// sifUpHeap(i);
// }
for(int i = _size / 2 ; i >=1 ; i--) //从最后一个结点开始调整
{
sifDownHeap_non(i);
}
}
向上调整算法和向下调整算法的比较
向上调整算法(Sift Up)和向下调整算法(Sift Down)是堆数据结构中常用的两种调整方法,它们各有特点和适用场景,无法简单地说哪个更优秀。选择使用哪种调整方法取决于具体的堆操作需求和上下文。下面分别介绍两者的特性及适用场景:
向上调整算法(Sift Up):
- 用途:通常用于将新插入的元素或被修改的元素调整到堆中的正确位置,使其满足堆性质(大根堆或小根堆)。例如,在插入新元素后,将其放在堆末尾,然后从该位置开始向上调整,确保新元素及其路径上的所有节点满足堆性质。
- 特点:从堆底部(新元素所在位置或被修改元素所在位置)开始,逐层向上比较父节点与子节点的值,若子节点值更适合堆顶(对于大根堆,子节点值更大;对于小根堆,子节点值更小),则交换二者,直至子节点成为堆顶或已满足堆性质。
优点:- 适用于插入操作和单元素修改后的调整,因为新元素或被修改元素的初始位置已知,可以直接从该位置开始调整。
- 调整过程中涉及的节点数量相对较少,时间复杂度为 O(log n),效率较高。
缺点:- 不适用于堆顶元素被删除后的调整,因为此时需要重新确定堆顶元素,且可能需要对多个子节点进行比较和调整。
向下调整算法(Sift Down):
- 用途:通常用于删除堆顶元素后重新调整堆,或在构建堆的过程中对整个堆进行调整。例如,在删除堆顶元素后,将堆末尾元素移至堆顶,然后从堆顶开始向下调整,确保所有节点满足堆性质。
- 特点:从堆顶开始,逐层向下比较父节点与子节点的值,若父节点值更适合堆底(对于大根堆,父节点值更小;对于小根堆,父节点值更大),则交换二者,直至父节点成为堆底或已满足堆性质。
优点:- 适用于堆顶元素被删除后的调整,因为此时堆顶元素已知,可以直接从该位置开始调整。
- 在构建堆的过程中,可以从最后一个非叶子节点开始逐个进行向下调整,确保整个堆满足堆性质。
缺点:- 对于插入操作或单元素修改后的调整,可能需要遍历到堆底才能找到新元素或被修改元素的最终位置,调整过程中涉及的节点数量可能较多。
综上所述,向上调整算法和向下调整算法各有优势,适用于不同的堆操作场景。在实际应用中,根据具体需求选择合适的调整方法,或者结合使用这两种方法,可以有效维护堆数据结构的性质,确保堆操作的高效性。因此,不能简单地说哪个更优秀,而应视具体情况灵活选用。
如果大家阅读完之后还是比较迷糊的话,可以点击这里,这里是我之前写的堆的博客,介绍的更为详细:
https://blog.csdn.net/qq_67693066/article/details/131544172


![Amazon云计算AWS之[5]关系数据库服务RDS](https://img-blog.csdnimg.cn/direct/c7e33d19d32141df9eeb3f9714c4bd2e.png)