目录
力扣494. 目标和
解析代码(path设置成全局)
解析代码(path设置全局)
力扣494. 目标和
494. 目标和
难度 中等
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
}
};解析代码(path设置成全局)
在动态规划部分写过这题,现在用DFS写一写。对于每个数,可以选择加上或减去它,依次枚举每一个数字,在每个数都被选择时检查得到的和是否等于目标值。如果等于,则记录结果。
在这一题中可以窥见path是设置成全局的好还是设置成递归参数好:
如果path是一个类型,如 int 设置成递归参数好,参数可以帮我们完成回溯,代码会简洁。
如果path是一个数组之类的,设置成全局好,如力扣257. 二叉树的所有路径,否则效率低。
class Solution {
int path, ret, _target;
public:
int findTargetSumWays(vector<int>& nums, int target) {
_target = target;
dfs(nums, 0);
return ret;
}
void dfs(vector<int>& nums, int pos)
{
if(pos == nums.size())
{
if(path == _target)
++ret;
return;
}
path += nums[pos]; // 加法
dfs(nums, pos + 1);
path -= nums[pos]; // 回溯
path -= nums[pos]; // 减法
dfs(nums, pos + 1);
path += nums[pos]; // 回溯
}
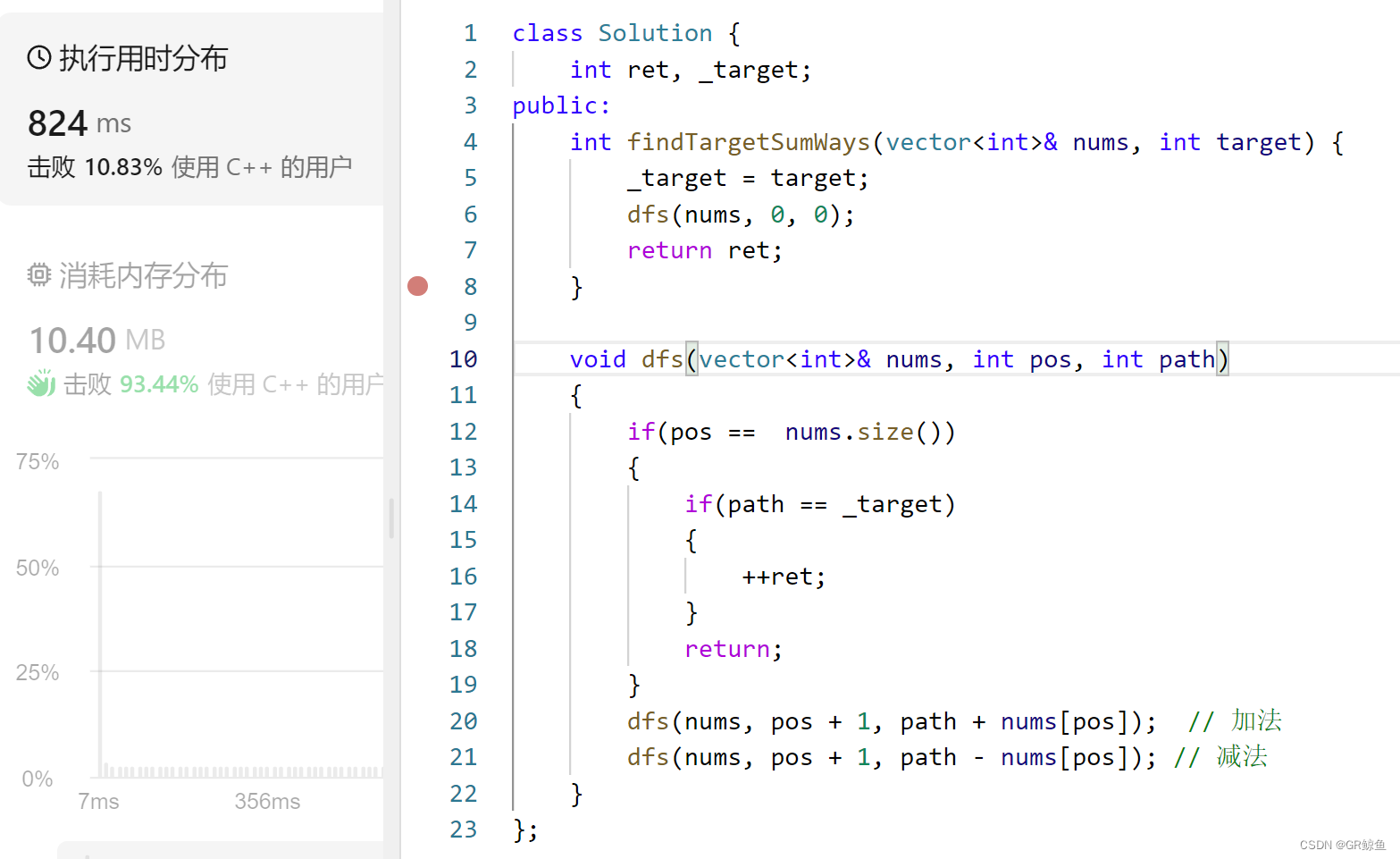
};解析代码(path设置全局)
此题path设置全局效率并没有提高很多,但是代码会简洁:
class Solution {
int ret, _target;
public:
int findTargetSumWays(vector<int>& nums, int target) {
_target = target;
dfs(nums, 0, 0);
return ret;
}
void dfs(vector<int>& nums, int pos, int path)
{
if(pos == nums.size())
{
if(path == _target)
++ret;
return;
}
dfs(nums, pos + 1, path + nums[pos]); // 加法
dfs(nums, pos + 1, path - nums[pos]); // 减法
}
};