目录
无向图
无向图度
无向图性质
有向图
有向图度
有向图性质
图的分类:
稀疏图:
稠密图:
零图:
有向完全图:
无向完全图:
度序列:
图是由顶点集合(简称点集)和顶点间的边(简称边集)组成的数据结构,通常用G(V,E)表示
用G=(V,E);表示一个图结构 V是点集,E是边集
有向边——>有向图 无向边——>无向图
无向图
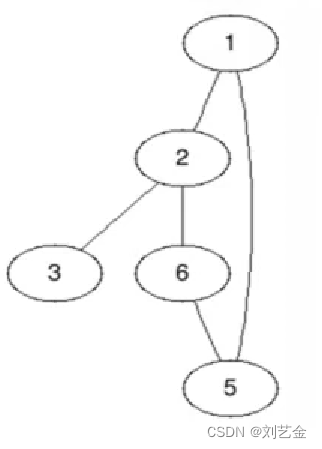
点集V(G)={1,2,3,4,5,6},边集E(G)={(1,2),{1,5},{2,3},{2,6},{5,6}}
无向图度
每个顶点的边数,如顶点1,度为2
无向图性质
顶点的度数总和为边数的两倍,因为对于同一条无向边,它会是两个顶点的度
有向图

点集V(G)={1,2,3,4,5,6},边集E(G)={(1,2),{2,3},{2,6},(6,5),{1,5}}
对于每一条边,称其为从u到v的一条有向边,u是有向边的起点,v是终点,注意在有向图中,(u,v)和(v,u)是不同的两条有向边
有向图度
入度:以该顶点为终点的有向边
出度:以该顶点为起点的有向边
如顶点1,入度0,出度2
有向图性质
所有入度等于所有出度
图的分类:
稀疏图:
边数少的叫稀疏图
稠密图:
边数多的叫稠密图
零图:
边数为空的是零图
有向完全图:
任意顶点间有两条边(u,v)和(v,u)相连
n个顶点n*2条边
无向完全图:
任意顶点间都有一条无向边
n个顶点有n*(n-1)/2条边
度序列:
定义:
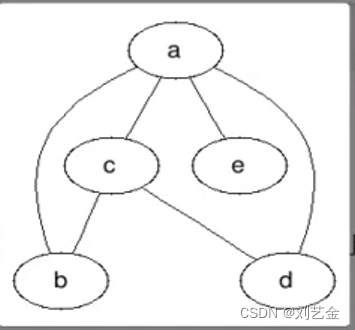
在无向图中,所有顶点的度数排成一个序列s,则称s为图G的度序列,
如abcde对应序列4,2,3,2,1。而1,2,2,3,4也是对应的度序列,每个无向图对应的度序列不是唯一的
用于判断一个序列是否可图: