题目1——括号匹配问题

题目来源. - 力扣（LeetCode）

思路——辅助栈法

括号匹配问题是一个经典的计算机科学问题，常用于检查一个字符串中的括号是否正确匹配。这包括各种括号，如小括号“()”，大括号“{}”，尖括号“<>”以及方括号“[]”。

这个问题可以通过使用栈（Stack）来解决，因为栈的后进先出（LIFO）特性使得我们可以很方便地处理嵌套结构。

以下是使用栈来解决括号匹配问题的基本思路：

1. 初始化一个空栈：这个栈将用于存储尚未找到匹配项的左括号。

2. 遍历输入字符串：对于字符串中的每个字符，我们执行以下操作：

   • 如果遇到左括号（如'(', '{', '<', '['），我们将其压入栈中。
   • 如果遇到右括号（如')', '}', '>', ']'），我们检查栈顶元素（如果存在）是否是对应的左括号。如果是，我们将栈顶元素弹出，表示找到了匹配项；如果不是或者栈为空，说明存在括号不匹配的情况，返回false。

3. 检查栈是否为空：在遍历完整个字符串后，如果栈为空，说明所有括号都找到了匹配项，返回true；否则，栈中剩余的左括号没有找到匹配项，返回false。

这个算法的时间复杂度是O(n)，其中n是输入字符串的长度，因为我们只需要遍历一次字符串。空间复杂度也是O(n)，在最坏的情况下，栈中可能存储n/2个左括号（假设所有括号都是左括号）。

队列（Queue）通常用于处理具有先进先出（FIFO）特性的问题，不适合用于解决括号匹配问题，因为队列无法方便地处理嵌套结构。

代码实现

bool isValid(char* s) 
{
    ST st;
    StackInit(&st);
    while(*s)
    {
        if (*s == '(' 
        || *s == '{' 
        || *s == '[')
        {
            StackPush(&st, *s);
            ++s;
        }
        else
        {
            //遇到右括号了，但是栈里面没有数据
            //说明前面没有左括号，不匹配
            if (StackEmpty(&st))
            {
                StackDestroy(&st);
                return false;
            }

            STDataType top = StackTop(&st);
            StackPop(&st);
            if ((*s == '}' && top != '{')
            || (*s == ']' && top != '[')
            || (*s == ')' && top != '('))
            {
                StackDestroy(&st);
                return false;
            }
            else
            {
                s++;
            }
        }
    }

    //如果栈不是空，说有栈中还有左括号未出
    bool ret = StackEmpty(&st);
    StackDestroy(&st);
    return ret;
}

题目2——用队列实现栈

题目来源. - 力扣（LeetCode）

思路 

这道题目是为初级读者准备的，题目涉及到栈和队列两种数据结构。

栈是一种后进先出的数据结构，元素从顶端入栈，然后从顶端出栈。

队列是一种先进先出的数据结构，元素从后端入队，然后从前端出队。

我们可以使用一个队列来实现这一想法

使用一个队列时，为了满足栈的特性，即最后入栈的元素最先出栈，同样需要满足队列前端的元素是最后入栈的元素。

入栈操作时，首先获得入栈前的元素个数 n，然后将元素入队到队列，再将队列中的前 n 个元素（即除了新入栈的元素之外的全部元素）依次出队并入队到队列，此时队列的前端的元素即为新入栈的元素，且队列的前端和后端分别对应栈顶和栈底。

由于每次入栈操作都确保队列的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可，获得栈顶元素操作只需要获得队列的前端元素并返回即可（不移除元素）。

由于队列用于存储栈内的元素，判断栈是否为空时，只需要判断队列是否为空即可。

代码实现

// 定义一个链表节点的结构体  
typedef struct tagListNode {  
    struct tagListNode* next;  // 指向下一个节点的指针  
    int val;                   // 节点的值  
} ListNode;  
  
// 定义一个栈的结构体  
typedef struct {  
    ListNode* top;  // 栈顶元素，指向栈顶节点的指针  
} MyStack;  
  
// 创建一个新的栈  
MyStack* myStackCreate() {  
    MyStack* stk = calloc(1, sizeof(MyStack));  // 使用calloc分配内存并初始化为0  
    return stk;  // 返回新创建的栈  
}  
  
// 向栈中压入一个元素  
void myStackPush(MyStack* obj, int x) {  
    ListNode* node = malloc(sizeof(ListNode));  // 为新节点分配内存  
    node->val = x;  // 设置新节点的值  
    node->next = obj->top;  // 新节点指向原来的栈顶  
    obj->top = node;  // 更新栈顶为新的节点  
}  
  
// 从栈中弹出并返回栈顶元素  
int myStackPop(MyStack* obj) {  
    ListNode* node = obj->top;  // 获取栈顶节点  
    int val = node->val;  // 获取栈顶节点的值  
    obj->top = node->next;  // 更新栈顶为下一个节点  
    free(node);  // 释放原来的栈顶节点  
    return val;  // 返回弹出的值  
}  
  
// 获取栈顶元素的值  
int myStackTop(MyStack* obj) {  
    return obj->top->val;  // 直接返回栈顶节点的值  
}  
  
// 判断栈是否为空  
bool myStackEmpty(MyStack* obj) {  
    return (obj->top == NULL);  // 如果栈顶为NULL，则栈为空  
}  
  
// 释放栈占用的内存  
void myStackFree(MyStack* obj) {  
    while (obj->top != NULL) {  // 当栈不为空时  
        ListNode* node = obj->top;  // 获取栈顶节点  
        obj->top = obj->top->next;  // 更新栈顶为下一个节点  
        free(node);  // 释放原来的栈顶节点  
    }  
    free(obj);  // 释放栈本身占用的内存  
}

题目3——用栈实现队列

题目来源. - 力扣（LeetCode）

 思路——双栈

使用栈来实现队列的原理主要基于两个栈的交互操作。栈（Stack）是一种后进先出（LIFO，Last In First Out）的数据结构，而队列（Queue）是一种先进先出（FIFO，First In First Out）的数据结构。因此，直接使用一个栈是无法实现队列的先进先出特性的。但是，通过两个栈的配合使用，我们可以模拟出队列的行为。

原理如下：

1. 定义两个栈：我们定义两个栈，stack1 和 stack2。stack1 只用于接收入队操作（enqueue）的元素，而 stack2 只用于执行出队操作（dequeue）。
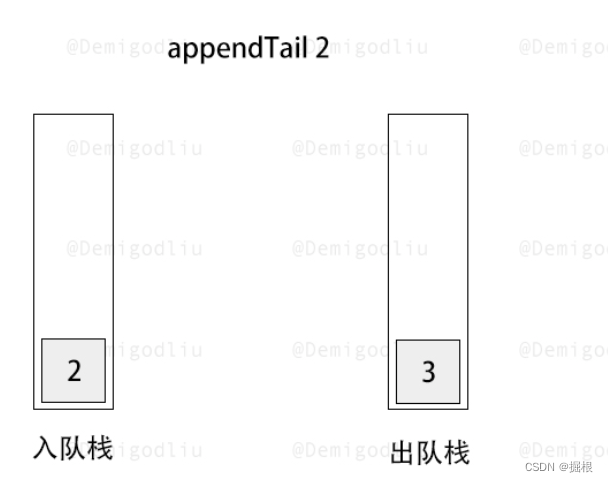
2. 入队操作：当需要进行入队操作时，我们直接将元素压入 stack1。此时，stack1 中的元素顺序是后进先出的，但我们还不能直接从 stack1 中弹出元素，因为这样会破坏队列的先进先出特性。
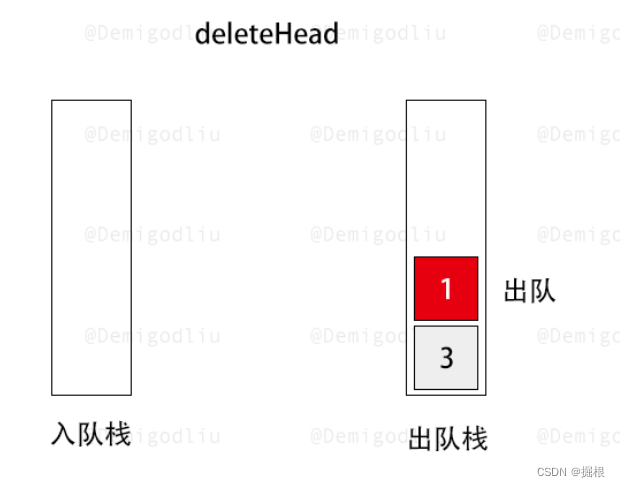
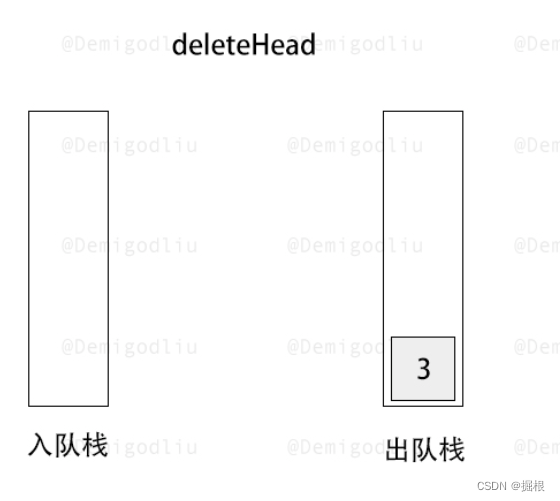
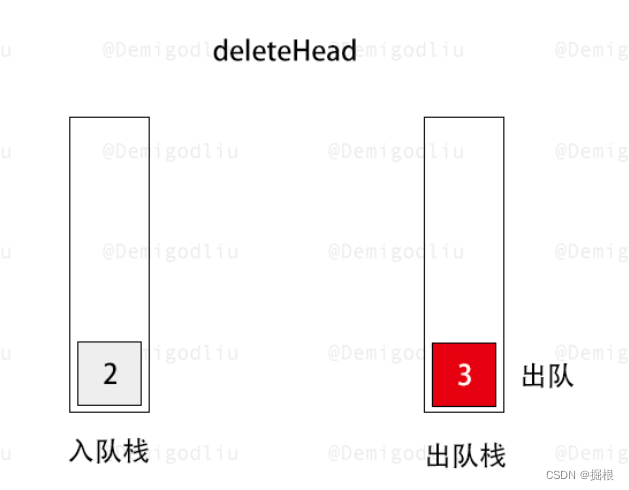
3. 出队操作：当需要进行出队操作时，我们首先检查 stack2 是否为空。如果 stack2 不为空，我们直接从 stack2 的栈顶弹出元素即可，因为 stack2 中的元素顺序已经是先进先出的了。但是，如果 stack2 为空，我们就需要将 stack1 中的所有元素逐个弹出并压入 stack2，这样 stack2 中的元素顺序就变成了先进先出。然后，我们再从 stack2 的栈顶弹出元素进行出队操作。

通过这种方式，我们可以保证队列的先进先出特性得以维持。虽然使用两个栈会增加一些操作的复杂性（特别是在 stack2 为空时需要将 stack1 中的元素全部转移到 stack2），但整体上这种方法是可以有效实现队列的。

需要注意的是，当队列为空时，stack1 和 stack2 都应该是空的。同时，为了优化性能，我们可以在入队时尽量避免不必要的元素转移操作。例如，当 stack2 不为空时，我们可以直接将新元素压入 stack2 而不是 stack1，这样可以减少后续出队时的元素转移次数。但是，这种方法需要更复杂的逻辑来控制两个栈的使用，因此在实际实现时需要根据具体需求进行权衡。

 

 

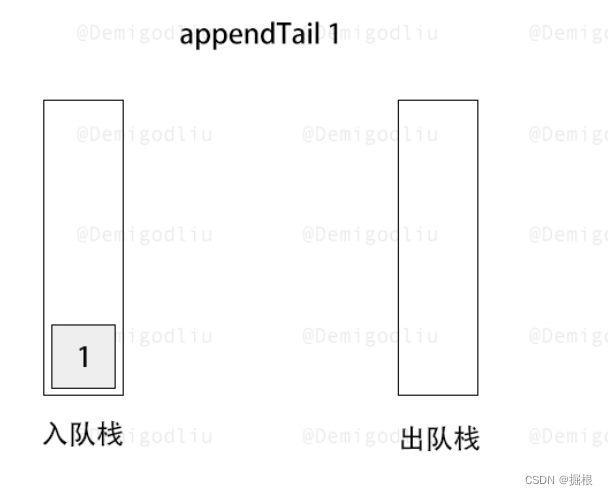
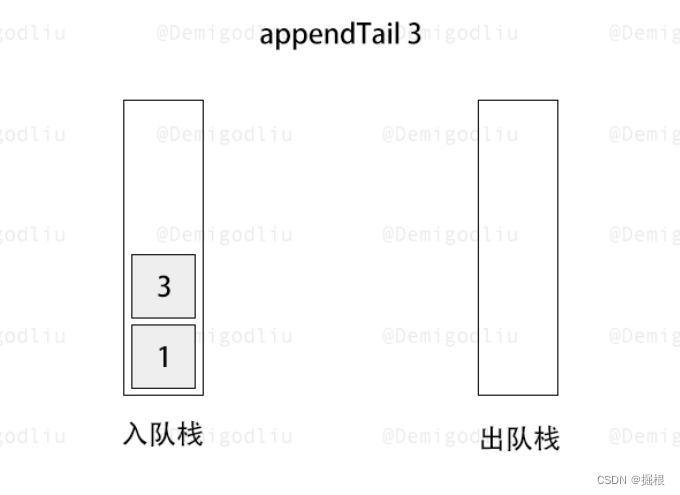
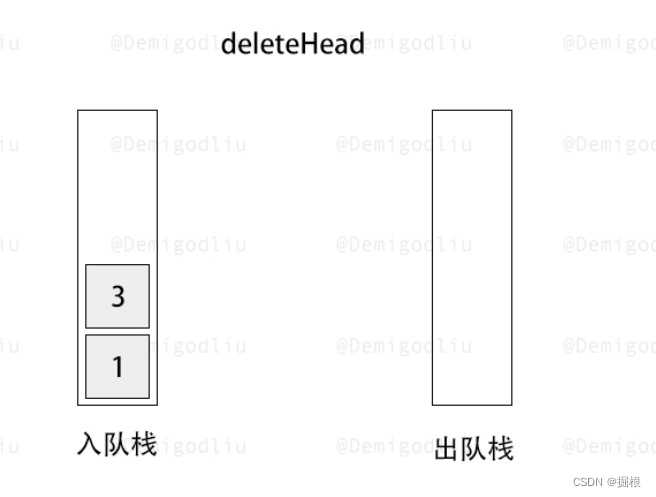
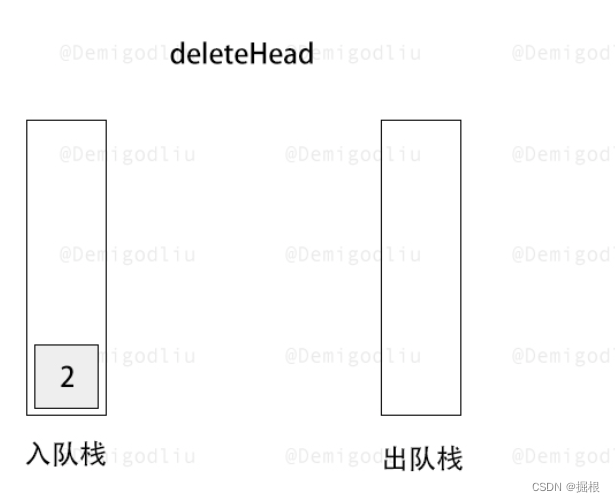
此时出队栈为空，所以要将入队栈的第一个进入的元素放入出队栈 

 

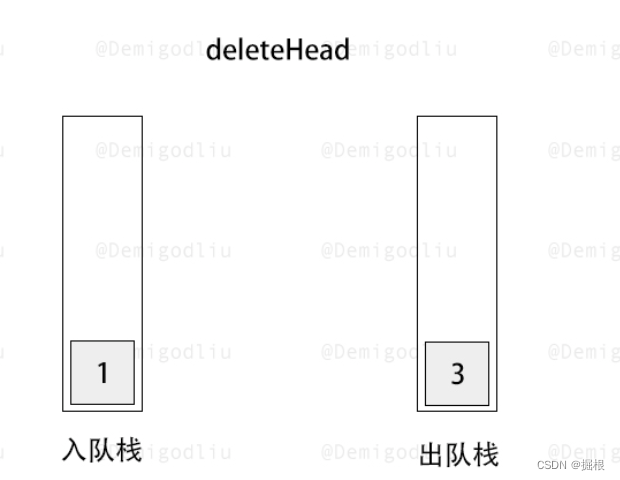
此时出队栈不为空，执行出队操作 

 

 

 

 

 

代码实现

typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;

// 定义队列的结构体  
typedef struct {  
    ST pushst; // 入队栈  
    ST popst;  // 出队栈  
} MyQueue;  
  
// 初始化队列  
MyQueue* myQueueCreate() {  
    MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));  
    if (obj == NULL) {  
        perror("malloc fail");  
        return NULL;  
    }  
    STInit(&obj->pushst); // 初始化入队栈  
    STInit(&obj->popst);  // 初始化出队栈  
    return obj;  
}  
  
// 入队操作  
void myQueuePush(MyQueue* obj, int x) {  
    STPush(&obj->pushst, x); // 将元素推入入队栈  
} 

// 查看队首元素  
int myQueuePeek(MyQueue* obj) {  
    if (STEmpty(&obj->popst)) {  
        // 如果出队栈为空，则将入队栈中的元素全部倒入出队栈  
        while (!STEmpty(&obj->pushst)) {  
            STPush(&obj->popst, STPop(&obj->pushst));  
        }  
    }  
    return STTop(&obj->popst); // 返回出队栈的栈顶元素  
}  
  
// 出队操作  
int myQueuePop(MyQueue* obj) {  
    int front = myQueuePeek(obj);  
    STPop(&obj->popst); // 弹出出队栈的栈顶元素  
    return front;  
}  
  
// 检查队列是否为空  
bool myQueueEmpty(MyQueue* obj) {  
    return STEmpty(&obj->pushst) && STEmpty(&obj->popst);  
}  
  
// 释放队列内存  
void myQueueFree(MyQueue* obj) {  
    STDestroy(&obj->pushst);  
    STDestroy(&obj->popst);  
    free(obj);  
}  

题目4——设计循环队列

题目来源. - 力扣（LeetCode）