问题列举

为什么我本地资源改变但是我在用 tomcat 预览网页时图片仍然未之前的图片?

为什么我当前网页的图片是之前的我换浏览器就变了?

tomcat启动后，为什么访问项目中的图片无效解决?

解决方案

问题一

为什么我本地资源改变但是我在用 tomcat 预览网页时图片仍然未之前的图片?

最主要问题的浏览器本地资源未更新

我们在做一个设计前端页面的时候要考虑的前端资源加载和浏览器缓存

下面列举解决方法

1. 手动更新浏览器资源

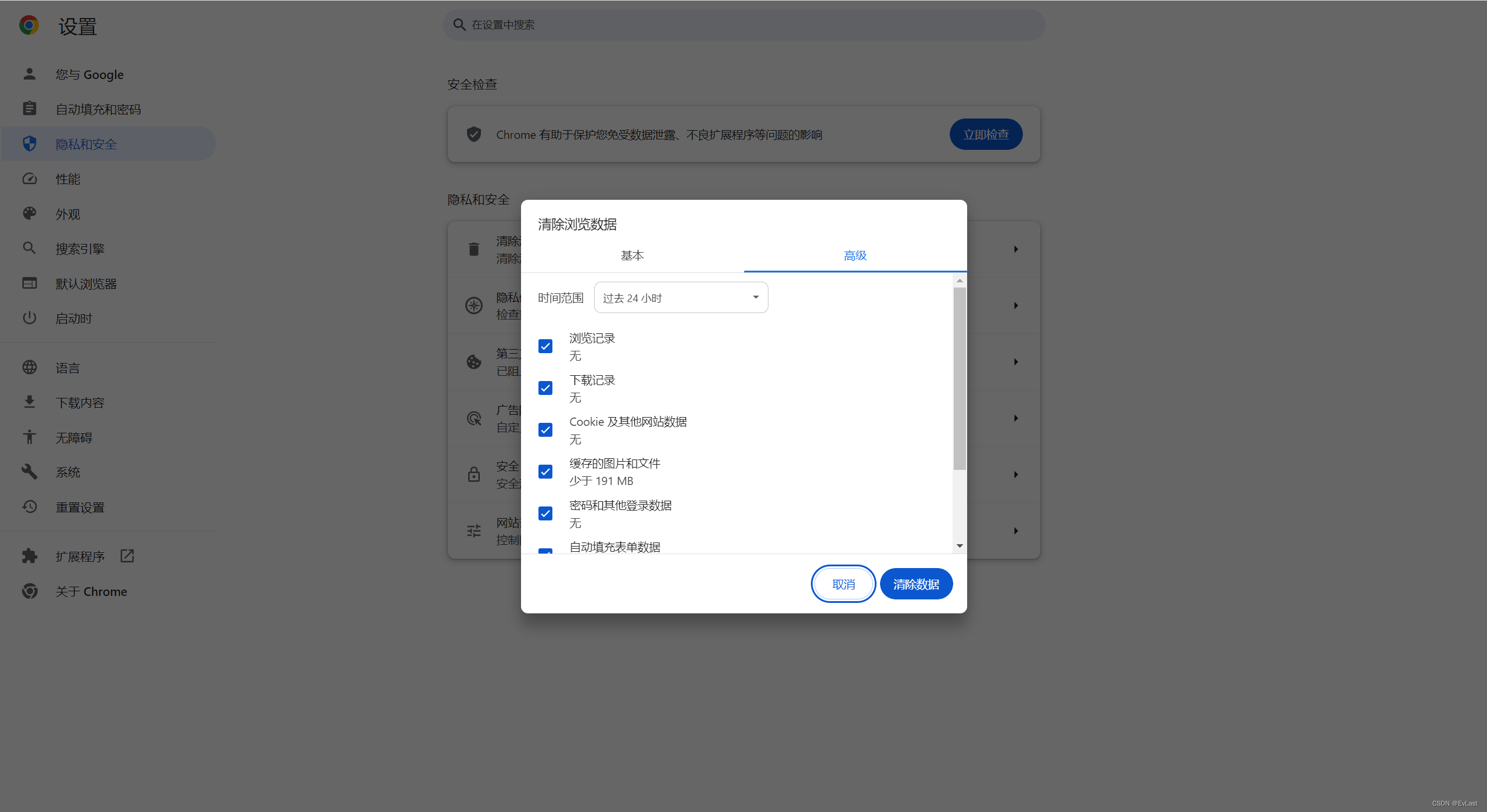
关于谷歌的更新方法

1.点击红色区域

2. 点击 清处浏览器数据
   
   3.点击清除数据 即可

关于Edge

可能刷新都可能会出现问题,这个时候需要定位元素按照元素访问相应的地址查看图片

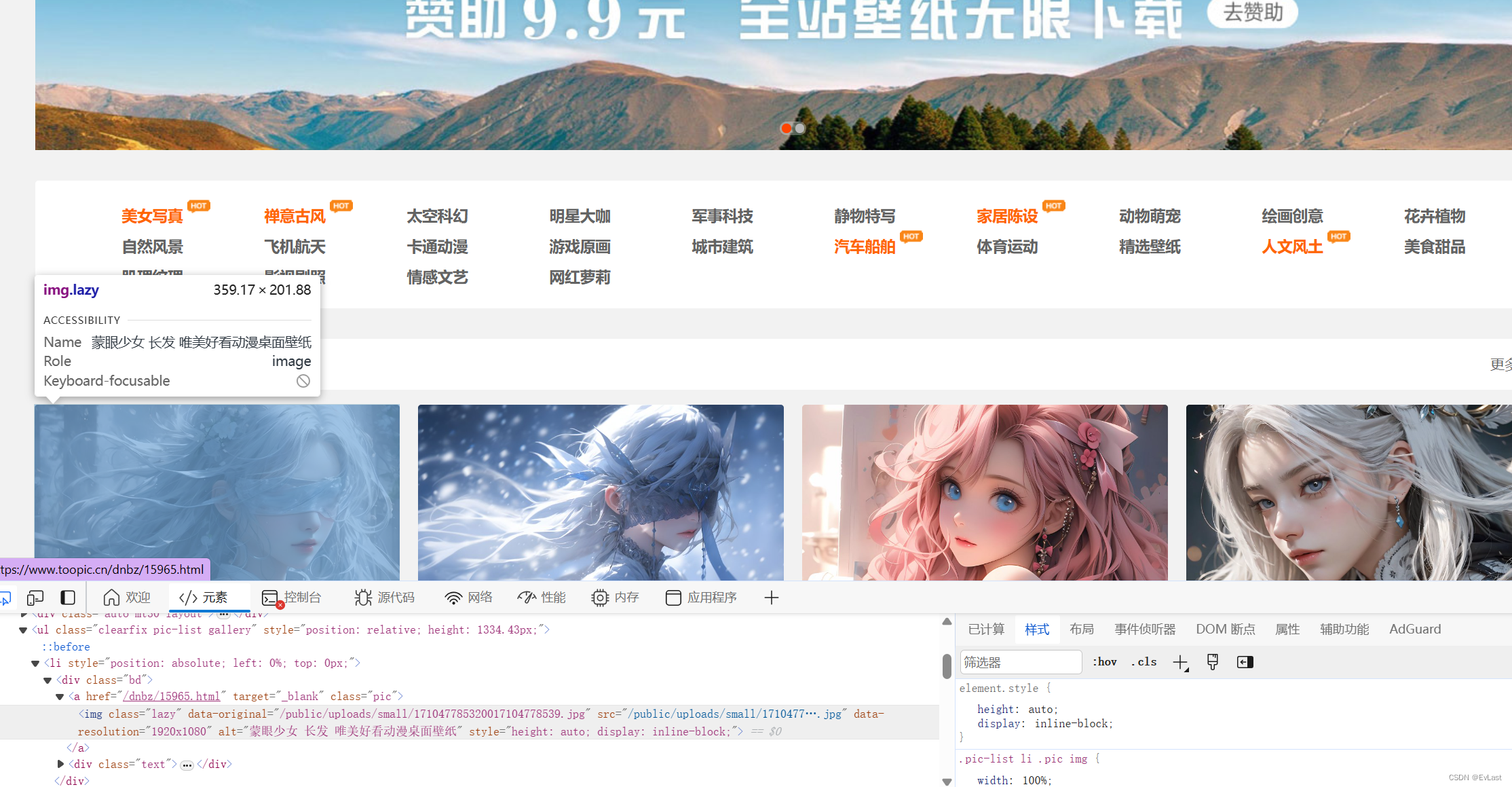
点击此处可以查看相应地址

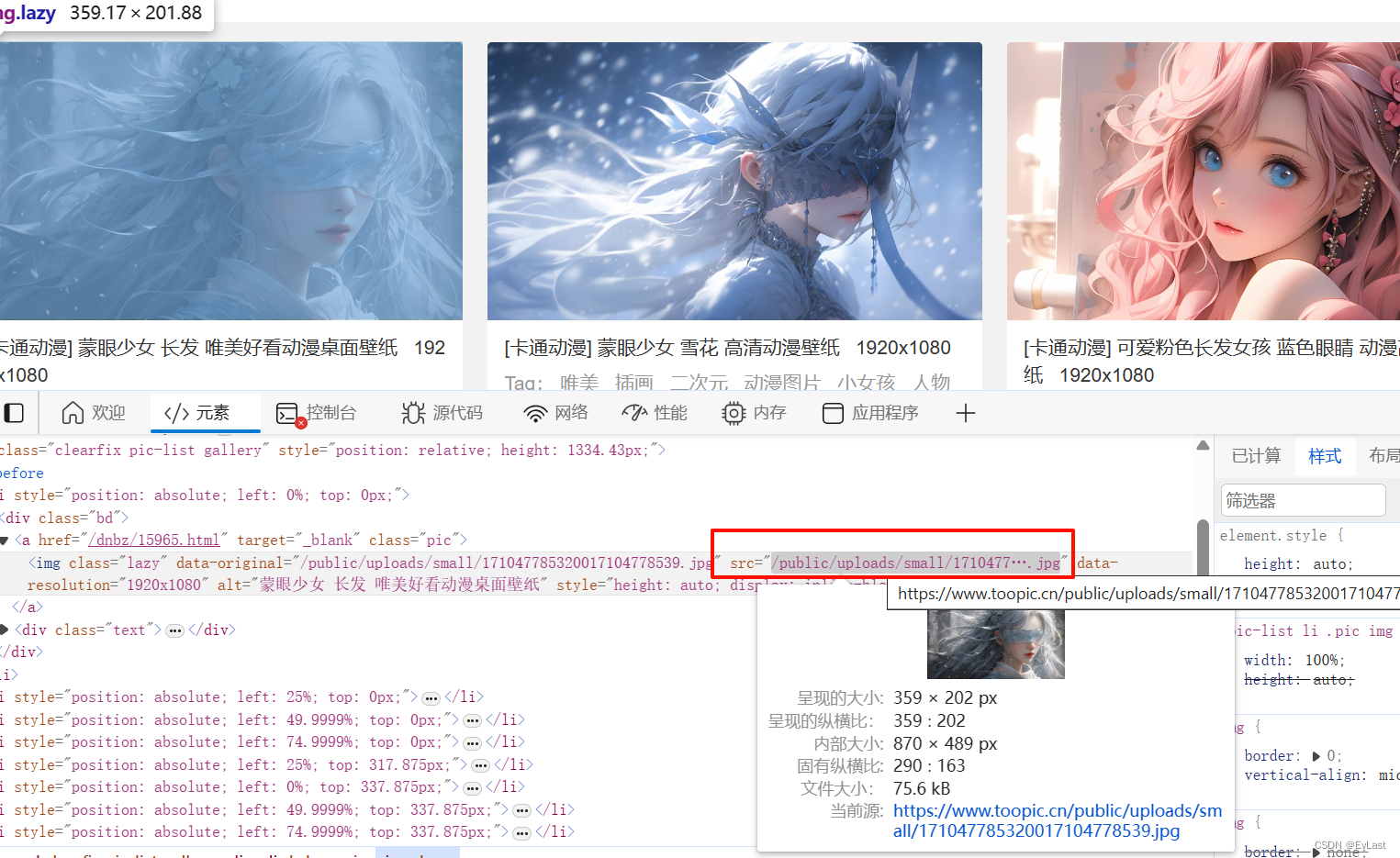
访问地址刷新即可会发现图片更新这个时候回到原页面刷新即可更新图片

如果对算法感兴趣可以加入相关QQ群进行交流: 787936200