通信原理(2)–随机过程
3.1随机过程的基本概念
随机过程{x(t)}由一族时间函数
x
i
(
t
)
x_i(t)
xi(t),i=1,2.3…组成,每一个时间函数
x
i
(
t
)
x_i(t)
xi(t)称为随机过程{x(t)}的一个样本函数(一个实现)
每个样本函数在时间上,在幅度取值上都是连续变化的波形。
若固定时刻,随机过程在该时刻所有样本函数的取值则为一随机变量。
为了描述随机过程在不同时刻的相互关系,用n维联合分布函数(概率密度函数族)来描述n个不同时刻对应的n个随机变量。


随机过程其实是随机变量在连续时间上的一次升维
3.1.1随机过程的分布函数
一维分布函数
F
1
(
x
1
,
t
1
)
=
P
[
ξ
(
t
1
)
≤
x
1
]
F_1(x_1,t_1)=P\Big[\xi(t_1)\leq x_1\Big]
F1(x1,t1)=P[ξ(t1)≤x1]
{ 0 ≤ F 1 ( x 1 , t 1 ) ≤ 1 F 1 ( − ∞ , t 1 ) = 0 , F 1 ( + ∞ , t 1 ) = 1 x 2 > x 1 , F 1 ( x 2 , t 1 ) > F 1 ( x 1 , t 1 ) \begin{cases}0\leq F_1(x_1,t_1)\leq1\\F_1(-\infty,t_1)=0,F_1(+\infty,t_1)=1\\x_2>x_1,F_1(x_2,t_1)>F_1(x_1,t_1)\end{cases} ⎩ ⎨ ⎧0≤F1(x1,t1)≤1F1(−∞,t1)=0,F1(+∞,t1)=1x2>x1,F1(x2,t1)>F1(x1,t1)
一维概率密度函数
f
1
(
x
1
,
t
1
)
=
∂
F
1
(
x
1
,
t
1
)
∂
x
1
f_1(x_1,t_1)=\frac{\partial F_1(x_1,t_1)}{\partial x_1}
f1(x1,t1)=∂x1∂F1(x1,t1)
{ f 1 ( x 1 , t 1 ) ≥ 0 F 1 ( x 1 , t 1 ) = ∫ − ∞ x 1 f 1 ( x 1 ′ , t 1 ) d x 1 ′ P [ a 1 ≤ ξ ( t 1 ) ≤ a 1 ] = ∫ a 1 a 2 f 1 ( x 1 , t 1 ) d x 1 ∫ − ∞ + ∞ f 1 ( x 1 , t 1 ) d x 1 = 1 \begin{cases}f_1(x_1,t_1)\geq0\\[2ex]F_1(x_1,t_1)=\int_{-\infty}^{x_1}f_1(x_1^{\prime},t_1)\mathrm{d}x_1^{\prime}\\[2ex]P\Big[a_1\leq\xi(t_1)\leq a_1\Big]=\int_{a_1}^{a_2}f_1(x_1,t_1)\mathrm{d}x_1\\[2ex]\int_{-\infty}^{+\infty}f_1(x_1,t_1)\mathrm{d}x_1=1\end{cases} ⎩ ⎨ ⎧f1(x1,t1)≥0F1(x1,t1)=∫−∞x1f1(x1′,t1)dx1′P[a1≤ξ(t1)≤a1]=∫a1a2f1(x1,t1)dx1∫−∞+∞f1(x1,t1)dx1=1
n维分布函数与n维概率密度函数
n维分布函数
F
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
,
t
2
,
⋯
,
t
n
)
=
P
[
ξ
(
t
1
)
≤
x
1
,
ξ
(
t
2
)
≤
x
2
,
⋯
,
ξ
(
t
n
)
≤
x
n
]
F_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=P\Big[\xi(t_1)\leq x_1,\xi(t_2)\leq x_2,\cdots,\xi(t_n)\leq x_n\Big]
Fn(x1,x2,⋯,xn;t1,t2,⋯,tn)=P[ξ(t1)≤x1,ξ(t2)≤x2,⋯,ξ(tn)≤xn]
n维概率密度函数
f
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
,
t
2
,
⋯
,
t
n
)
=
∂
F
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
,
t
2
,
⋯
,
t
n
)
∂
x
1
∂
x
2
⋯
∂
x
n
f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=\frac{\partial F_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)}{\partial x_1\partial x_2\cdots\partial x_n}
fn(x1,x2,⋯,xn;t1,t2,⋯,tn)=∂x1∂x2⋯∂xn∂Fn(x1,x2,⋯,xn;t1,t2,⋯,tn)
数学期望
a ( t ) = E [ ξ ( t ) ] = ∫ − ∞ + ∞ x f 1 ( x , t ) d x a(t)=E\Big[\xi(t)\Big]=\int_{-\infty}^{+\infty}xf_1(x,t)\mathrm{d}x a(t)=E[ξ(t)]=∫−∞+∞xf1(x,t)dx
道机过程的数学期望与t有关,表示n个样本函数曲线的摆动中心。
E[C]=C常数的数学期望是常数本身:
E
[
a
X
1
+
b
X
2
]
=
a
E
[
X
1
]
+
b
E
[
X
2
]
E\left[aX_1+bX_2\right]=aE\left[X_1\right]+bE\left[X_2\right]
E[aX1+bX2]=aE[X1]+bE[X2]
对于两个统计独立的随机变量
X
1
,
X
2
,有
E
[
X
1
X
2
]
=
E
[
X
1
]
E
[
X
2
]
X_1,X_2\text{,有}E[X_1X_2]=E[X_1]E[X_2]
X1,X2,有E[X1X2]=E[X1]E[X2]
方差
D [ ξ ( t ) ] = E { [ ξ ( t ) − a ( t ) ] 2 } = E [ ξ 2 ( t ) ] − a 2 ( t ) D\Big[\xi(t)\Big]=E\Big\{\Big[\xi(t)-a(t)\Big]^2\Big\}=E\Big[\xi^2(t)\Big]-a^2(t) D[ξ(t)]=E{[ξ(t)−a(t)]2}=E[ξ2(t)]−a2(t)
随机过程的方差表示了随机过程 ξ ( t ) \xi(t) ξ(t)在t时刻偏离数学期望的程度。
D [ C ] = 0 D[C]=0 D[C]=0 常数的方差是0;
D
[
C
X
]
=
C
2
D
[
X
]
,
D
[
X
+
C
]
=
D
[
X
]
D[CX]=C^{2}D[X],\:D[X+C]=D[X]
D[CX]=C2D[X],D[X+C]=D[X]
对于两个随机变量
X
1
,
X
2
X_1,X_2
X1,X2, 有
D
[
a
X
1
+
b
X
2
]
=
a
2
D
[
X
1
]
+
b
2
D
[
X
2
]
+
2
a
b
⋅
C
o
v
[
X
1
,
X
2
]
D\left[aX_1+bX_2\right]=a^2D\left[X_1\right]+b^2D\left[X_2\right]+2ab\cdot\mathrm{Cov}\left[X_1,X_2\right]
D[aX1+bX2]=a2D[X1]+b2D[X2]+2ab⋅Cov[X1,X2]
对于两个不相关的随机变量
X
1
,
X
2
X_1,X_2
X1,X2, 有
D [ a X 1 + b X 2 ] = a 2 D [ X 1 ] + b 2 D [ X 2 ] D\Big[aX_1+bX_2\Big]=a^2D\Big[X_1\Big]+b^2D\Big[X_2\Big] D[aX1+bX2]=a2D[X1]+b2D[X2]
3.1.2随机过程的统计特性
数学期望和方差只能反映随机变量
ξ
(
t
)
\xi(t)
ξ(t)在孤立时刻的数字特征,不
能反映不同时刻的内在联系。
- 自相关函数
R ( t 1 , t 2 ) = E [ ξ ( t 1 ) ξ ( t 2 ) ] = ∫ − ∞ + ∞ ∫ − ∞ + ∞ x 1 x 2 f 2 ( x 1 , x 2 ; t 1 , t 2 ) d x 1 d x 2 R(t_{1},t_{2})=E\Big[\xi(t_{1})\xi(t_{2})\Big]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x_{1}x_{2}f_{2}(x_{1},x_{2};t_{1},t_{2})\mathrm{d}x_{1}\mathrm{d}x_{2} R(t1,t2)=E[ξ(t1)ξ(t2)]=∫−∞+∞∫−∞+∞x1x2f2(x1,x2;t1,t2)dx1dx2
反映不同时刻随机过程取值的相关性。
- 自协方差函数
B ( t 1 , t 2 ) = E { [ ξ ( t 1 ) − a ( t 1 ) ] [ ξ ( t 2 ) − a ( t 2 ) ] } B(t_1,t_2)=E\left\{\left[\xi(t_1)-a(t_1)\right]\left[\xi(t_2)-a(t_2)\right]\right\} B(t1,t2)=E{[ξ(t1)−a(t1)][ξ(t2)−a(t2)]}
= ∫ − ∞ + ∞ ∫ − ∞ + ∞ [ x 1 − a ( t 1 ) ] [ x 2 − a ( t 2 ) ] f 2 ( x 1 , x 2 ; t 1 , t 2 ) d x 1 d x 2 =\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\Big[x_{1}-a(t_{1})\Big]\Big[x_{2}-a(t_{2})\Big]f_{2}(x_{1},x_{2};t_{1},t_{2})\mathrm{d}x_{1}\mathrm{d}x_{2} =∫−∞+∞∫−∞+∞[x1−a(t1)][x2−a(t2)]f2(x1,x2;t1,t2)dx1dx2
自协方差函数反映不同时刻随机过程的统计相关性。
- 自相关函数与自协方差函数的关系
B ( t 1 , t 2 ) = R ( t 1 , t 2 ) − a ( t 1 ) a ( t 2 ) B(t_1,t_2)=R(t_1,t_2)-a(t_1)a(t_2) B(t1,t2)=R(t1,t2)−a(t1)a(t2)
对于零均值随机过程:
B
(
t
1
,
t
2
)
=
R
(
t
1
,
t
2
)
B(t_1,t_2)=R(t_1,t_2)
B(t1,t2)=R(t1,t2)
假定
t
2
>
t
1
t_2>t_1
t2>t1,令
t
2
=
t
1
+
τ
t_2=t_1+\tau
t2=t1+τ,则
R
(
t
1
,
t
2
)
=
R
(
t
1
,
t
1
+
τ
)
;
R(t_1,t_2)=R(t_1,t_1+\tau)\:;
R(t1,t2)=R(t1,t1+τ);
我们一般研究时间间隔 τ \tau τ 对相关性的影响;
一般情况下, τ \tau τ越大,相关性越小
对于两个随机过程 ξ ( t ) \xi(t) ξ(t)和 η ( t ) \eta(t) η(t), 定义:
互相关函数
R
ξ
η
(
t
1
,
t
2
)
=
E
[
ξ
(
t
1
)
η
(
t
2
)
]
R_{\xi\eta}(t_1,t_2)=E\left[\xi(t_1)\eta(t_2)\right]
Rξη(t1,t2)=E[ξ(t1)η(t2)]
互协方差函数
B
ξ
η
(
t
1
,
t
2
)
=
E
{
[
ξ
(
t
1
)
−
a
ξ
(
t
1
)
]
[
η
(
t
2
)
−
a
η
(
t
2
)
]
}
B_{\xi\eta}(t_1,t_2)=E\left\{\left[\xi(t_1)-a_\xi(t_1)\right]\left[\eta(t_2)-a_\eta(t_2)\right]\right\}
Bξη(t1,t2)=E{[ξ(t1)−aξ(t1)][η(t2)−aη(t2)]}
3.2平稳随机过程
3.2.1定义
平稳随机过程的统计特性不随时间的推移而变化,其一维分布与时间 t t t 无关,二维分布只与时间间隔 τ \tau τ 有关。即:
一维分布与时间t无关
f
1
(
x
,
t
)
=
f
1
(
x
,
t
+
h
)
=
f
1
(
x
)
∀
h
f_1(x,t)=f_1(x,t+h)=f_1(x)\quad\forall h
f1(x,t)=f1(x,t+h)=f1(x)∀h
二维分布只与时间间隔
τ
\tau
τ有关
f
2
(
x
1
,
x
2
;
t
1
,
t
2
)
=
f
2
(
x
1
,
x
2
;
t
1
+
h
,
t
2
+
h
)
f_2(x_1,x_2;t_1,t_2)=f_2(x_1,x_2;t_1+h,t_2+h)
f2(x1,x2;t1,t2)=f2(x1,x2;t1+h,t2+h)
= f 2 ( x 1 , x 2 ; t 2 − t 1 ) = f 2 ( x 1 , x 2 ; τ ) ∀ h =f_2(x_1,x_2;t_2-t_1)=f_2(x_1,x_2;\tau)\quad\forall h =f2(x1,x2;t2−t1)=f2(x1,x2;τ)∀h
3.2.2 平稳随机过程的数字特征
均值: E [ ξ ( t ) ] = ∫ − ∞ + ∞ x f 1 ( x ) E\left [ \xi( t) \right ] = \int _{- \infty}^{+ \infty}xf_{1}( x) E[ξ(t)]=∫−∞+∞xf1(x)d x = α x= \alpha x=α 与 t t t无关,样本函数围绕一水平线起伏
方差: D [ ξ ( t ) ] = ∫ − α + ∞ ( x − a ) 2 f 1 ( x ) D\left [ \xi( t) \right ] = \int _{- \alpha}^{+ \infty}( x- a) ^{2}f_{1}( x) D[ξ(t)]=∫−α+∞(x−a)2f1(x)d x = E [ ξ 2 ( t ) ] − a 2 = σ 2 x= E\left [ \xi^2( t) \right ] - a^{2}= \sigma^{2} x=E[ξ2(t)]−a2=σ2 与== t t t无关==,为常数
自相关函数:
R ( t , t + τ ) = E [ ξ ( t ) ξ ( t + τ ) ] R(t,t+\tau)=E\bigl[\xi(t)\xi(t+\tau)\bigr] R(t,t+τ)=E[ξ(t)ξ(t+τ)]
=
∫
−
∞
+
∞
∫
−
∞
+
∞
x
1
x
2
f
2
(
x
1
,
x
2
;
τ
)
= \int _{- \infty}^{+ \infty}\int _{- \infty}^{+ \infty}x_{1}x_{2}f_{2}( x_{1}, x_{2}; \tau)
=∫−∞+∞∫−∞+∞x1x2f2(x1,x2;τ)d
x
1
x_1
x1d
x
2
=
R
(
τ
)
x_2= R( \tau)
x2=R(τ)
自相关只与时间间隔
τ
\tau
τ有关,而与时间起点无关。
3.2.3 狭义(严)平稳和广义(宽)平稳
- 狭义平稳随机过程(严平稳)
随机过程的各维概率密度函数都不随时间的推移而变化。
f
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
,
t
2
,
⋯
,
t
n
)
=
f
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
+
h
,
t
2
+
h
,
⋯
,
t
n
+
h
)
,
∀
n
,
h
f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=f_n(x_1,x_2,\cdots,x_n;t_1+h,t_2+h,\cdots,t_n+h),\:\forall n,h
fn(x1,x2,⋯,xn;t1,t2,⋯,tn)=fn(x1,x2,⋯,xn;t1+h,t2+h,⋯,tn+h),∀n,h
狭义平稳过程又称严平稳过程,条件很强,对其作放宽,可得广义平稳、即宽平稳过程的概念。
- 广义平稳随机过程(宽平稳)
一个二阶矩随机过程,均值为常数,自相关函数仅仅是时间间隔的函数,称这样的过程为广义平稳随机过程或宽平稳随机过程。
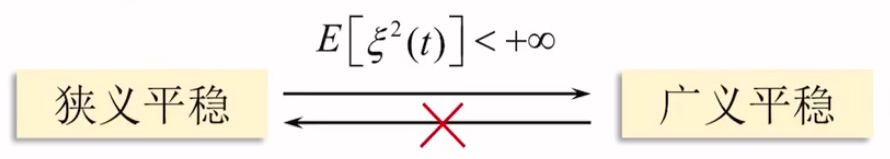
后文的平稳随机过程均为宽平稳(除特指)
3.2.3各态历经性
- 平稳随机过程的各态经历性
假定 x ( t ) x(t) x(t)为随机过程 ξ ( t ) \xi(t) ξ(t) 的任意一个实现,其时间均值和时间相关函数分别为:
a
‾
=
x
(
t
)
‾
=
lim
T
→
∞
1
T
∫
−
T
/
2
T
/
2
x
(
t
)
d
t
R
(
τ
)
‾
=
x
(
t
)
x
(
t
+
τ
)
‾
=
lim
T
→
∞
1
T
∫
−
T
/
2
T
/
2
x
(
t
)
x
(
t
+
τ
)
d
t
\overline{a}=\overline{x(t)}=\lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2}x(t)\mathrm{d}t\quad\overline{R(\tau)}=\overline{x(t)x(t+\tau)}=\lim_{T\to\infty}\frac{1}{T}\int_{-T/2}^{T/2}x(t)x(t+\tau)\mathrm{d}t
a=x(t)=T→∞limT1∫−T/2T/2x(t)dtR(τ)=x(t)x(t+τ)=T→∞limT1∫−T/2T/2x(t)x(t+τ)dt
若平稳随机过程依概率1满足
a
ˉ
=
a
\bar{a}=a
aˉ=a,
R
(
τ
)
‾
=
R
(
τ
)
\overline{R(\tau)}=R(\tau)
R(τ)=R(τ)
则称该平稳过程具有各态历经性。
- 含义
随机过程中任一实现都经历了随机过程的所有可能状态。
化“统计平均”为“时间平均”, 用任意一个样本函数刻画整个随机过程的所有特征,简化实际的测量和计算。
3.2.4平稳过程的自相关函数
3.2.4.1平稳随机过程自相关函数的性质
R ( 0 ) = E [ ξ 2 ( t ) ] = S R(0)=E\left[\xi^2(t)\right]=S R(0)=E[ξ2(t)]=S 物理意义:随机过程的平均功率;
R ( ∞ ) = E 2 [ ξ ( t ) ] = a 2 R(\infty)=E^2\left[\xi(t)\right]=a^2 R(∞)=E2[ξ(t)]=a2 物理意义:随机过程的直流功率;
时间间隔无限大时, ξ ( t ) \xi(t) ξ(t) 与 ξ ( t + τ ) \xi(t+\tau) ξ(t+τ)趋于独立
由于平稳, E [ ξ ( t + τ ) ] = E [ ξ ( t ) ] E\Big[\xi(t+\tau)\Big]=E\Big[\xi(t)\Big] E[ξ(t+τ)]=E[ξ(t)]
R ( ∞ ) = lim τ → α E [ ξ ( t ) ξ ( t + τ ) ] = lim τ → ∞ E [ ξ ( t ) ] E [ ξ ( t + τ ) ] = E [ ξ ( t ) ] E [ ξ ( t ) ] = E 2 [ ξ ( t ) ] R(\infty)=\lim_{\tau\to\alpha}E\left[\xi(t)\xi(t+\tau)\right]=\lim_{\tau\to\infty}E\left[\xi(t)\right]E\left[\xi(t+\tau)\right]=E\left[\xi(t)\right]E\left[\xi(t)\right]=E^2\left[\xi(t)\right] R(∞)=limτ→αE[ξ(t)ξ(t+τ)]=limτ→∞E[ξ(t)]E[ξ(t+τ)]=E[ξ(t)]E[ξ(t)]=E2[ξ(t)]
R ( 0 ) − R ( ∞ ) = E [ ξ 2 ( t ) ] − α 2 = σ 2 R(0)-R(\infty)=E\Bigl[\xi^2(t)\Bigr]-\alpha^2=\sigma^2 R(0)−R(∞)=E[ξ2(t)]−α2=σ2 物理意义:随机过程的交流功率;对应方差公式 D [ ξ ( t ) ] = E [ ξ 2 ( t ) ] − E 2 [ ξ ( t ) ] D[\xi(t)]=E\Big[\xi^2(t)\Big]-E^2\Big[\xi(t)\Big] D[ξ(t)]=E[ξ2(t)]−E2[ξ(t)]
R ( τ ) = R ( − τ ) R(\tau)=R(-\tau) R(τ)=R(−τ) 自相关函数为偶函数;
∣ R ( τ ) ∣ ≤ R ( 0 ) \begin{vmatrix}R(\tau)\end{vmatrix}\leq R(0)\quad R(τ) ≤R(0)给出了自相关函数的上界,与自身时刻相关性最大。
3.2.5平稳过程的功率谱密度
- 定义
假定 f ( t ) f(t) f(t)为随机过程 ξ ( t ) \xi(t) ξ(t)的任一实现,对其进行 T T T 长度的截断,记
为 f r ( t ) f_r(t) fr(t),其傅里叶变换为 F T ( ω ) F_T(\omega) FT(ω),则任一实现的功率谱为:
P f ( ω ) = lim T → ∞ ∣ F T ( ω ) ∣ 2 T P_f(\omega)=\lim_{T\to\infty}\frac{\left|F_T(\omega)\right|^2}T Pf(ω)=T→∞limT∣FT(ω)∣2
故 ξ ( t ) \xi(t) ξ(t) 的功率谱密度为:
- 维纳-辛钦定理
平稳随机过程 ξ ( t ) \xi(t) ξ(t)的功率谱密度函数 P ξ ( ω ) P_\xi(\omega) Pξ(ω)和自相关函数 R ( τ ) R(\tau) R(τ)为一对傅里叶变换对
{ P ξ ( ω ) = ∫ − ∞ + ∞ R ( τ ) e − j ω τ d τ R ( τ ) = 1 2 π ∫ − ∞ + ∞ P ξ ( ω ) e j ω τ d ω 或 { P ξ ( f ) = ∫ − ∞ + ∞ R ( τ ) e − j 2 π f τ d τ R ( τ ) = ∫ − ∞ + ∞ P ξ ( f ) e j 2 π f τ d f R ( τ ) ⇔ P ξ ( f ) \begin{cases}P_{\xi}(\omega)=\int_{-\infty}^{+\infty}R(\tau)e^{-j\omega\tau}\mathrm{d}\tau\\R(\tau)=\dfrac{1}{2\pi}\int_{-\infty}^{+\infty}P_{\xi}(\omega)e^{j\omega\tau}\mathrm{d}\omega\end{cases}\text{或}\begin{cases}P_{\xi}(f)=\int_{-\infty}^{+\infty}R(\tau)e^{-j2\pi f\tau}\mathrm{d}\tau\\R(\tau)=\int_{-\infty}^{+\infty}P_{\xi}(f)e^{j2\pi f\tau}\mathrm{d}f\end{cases}R(\tau)\Leftrightarrow P_{\xi}(f) ⎩ ⎨ ⎧Pξ(ω)=∫−∞+∞R(τ)e−jωτdτR(τ)=2π1∫−∞+∞Pξ(ω)ejωτdω或{Pξ(f)=∫−∞+∞R(τ)e−j2πfτdτR(τ)=∫−∞+∞Pξ(f)ej2πfτdfR(τ)⇔Pξ(f)
- 功率谱密度的性质
功率谱密度具有非负性: P ξ ( f ) ≥ 0 P_\xi(f)\geq0 Pξ(f)≥0
功率谱密度是偶函数 : P ξ ( − f ) = P ξ ( f ) :P_\xi(-f)=P_\xi(f) :Pξ(−f)=Pξ(f) ·
单边、双边功率谱密度互换: P ξ 单边 ( f ) = { 2 P ξ 双边 ( f ) f ≥ 0 0 f < 0 P_{\xi\text{单边}}(f)=\begin{cases}2P_{\xi\text{双边}}(f)&f\geq0\\0&f<0&\end{cases} Pξ单边(f)={2Pξ双边(f)0f≥0f<0
平均功率的计算方法
S
=
R
(
0
)
=
E
[
ξ
2
(
t
)
]
S
=
∫
−
∞
+
∞
P
ξ
(
f
)
d
f
=
1
2
π
∫
−
∞
+
∞
P
ξ
(
ω
)
d
ω
S=R(0)=E\bigg[\xi^2(t)\bigg]\quad S=\int_{-\infty}^{+\infty}P_\xi(f)\mathrm{d}f=\frac{1}{2\pi}\int_{-\infty}^{+\infty}P_\xi(\omega)\mathrm{d}\omega
S=R(0)=E[ξ2(t)]S=∫−∞+∞Pξ(f)df=2π1∫−∞+∞Pξ(ω)dω
3.3高斯随机过程
3.3.1定义
若随机过程的任意n维分布都是正态分布,则称它为高斯随机过程或正态过程。其n维概率密度函数为==(了解)==:
f
n
(
x
1
,
x
2
,
⋯
,
x
n
;
t
1
,
t
2
,
⋯
,
t
n
)
=
1
(
2
π
)
n
/
2
σ
1
σ
2
⋯
σ
n
∣
B
∣
1
/
2
exp
[
−
1
2
∣
B
∣
∑
j
=
1
n
∑
k
=
1
n
∣
B
j
k
∣
(
x
j
−
a
j
σ
j
)
(
x
k
−
a
k
σ
k
)
]
\begin{aligned}&f_{n}(x_{1},x_{2},\cdots,x_{n};t_{1},t_{2},\cdots,t_{n})\\&=\frac{1}{\left(2\pi\right)^{n/2}\sigma_{1}\sigma_{2}\cdots\sigma_{n}\left|B\right|^{1/2}}\exp\left[-\frac{1}{2\left|B\right|}\sum_{j=1}^{n}\sum_{k=1}^{n}\left|B_{jk}\right|\left(\frac{x_{j}-a_{j}}{\sigma_{j}}\right)\left(\frac{x_{k}-a_{k}}{\sigma_{k}}\right)\right]\end{aligned}
fn(x1,x2,⋯,xn;t1,t2,⋯,tn)=(2π)n/2σ1σ2⋯σn∣B∣1/21exp[−2∣B∣1j=1∑nk=1∑n∣Bjk∣(σjxj−aj)(σkxk−ak)]
3.3.2重要性质
- 高斯过程的n维分布完全由n个随机变量 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn的数学期望,方差以及两两变量之间的归一化协方差函数决定;
- 广义平稳的高斯过程也狭义平稳;
- 高斯过程在不同时刻取值不相关,则它们也统计独立:
f n ( x 1 , x 2 , ⋯ , x n ; t 1 , t 2 , ⋯ , t n ) = f ( x 1 , t 1 ) f ( x 2 , t 2 ) ⋯ f ( x n , t n ) f_n(x_1,x_2,\cdots,x_n;t_1,t_2,\cdots,t_n)=f(x_1,t_1)f(x_2,t_2)\cdots f(x_n,t_n) fn(x1,x2,⋯,xn;t1,t2,⋯,tn)=f(x1,t1)f(x2,t2)⋯f(xn,tn)
对于高斯变量来说,不相关和独立是等价的;
- 高斯过程经过线性变换(或线性系统)后仍为高斯过程,但数字特征发生改变:
- 若干个高斯过程的代数和仍为高斯过程,但数字特征发生改变。
X 1 ∼ N ( μ 1 , σ 1 2 ) , X 2 ∼ N ( μ 2 , σ 2 2 ) ⟶ a X 1 + b X 2 ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) X_1\sim N(\mu_1,\sigma_1^2),X_2\sim N(\mu_2,\sigma_2^2)\boxed{\longrightarrow}aX_1+bX_2\sim N(a\mu_1+b\mu_2,a^2\sigma_1^2+b^2\sigma_2^2) X1∼N(μ1,σ12),X2∼N(μ2,σ22)⟶aX1+bX2∼N(aμ1+bμ2,a2σ12+b2σ22)
3.3.3一维高斯过程
3.3.3.1概率密度函数与数字特征
f ( x ) = 1 2 π σ exp [ − ( x − a ) 2 2 σ 2 ] , − ∞ < x < + ∞ ⟹ X ∼ N ( a , σ 2 ) f(x)=\frac1{\sqrt{2\pi}\sigma}\exp\biggl[-\frac{(x-a)^2}{2\sigma^2}\biggr],-\infty<x<+\infty\quad\boxed{\Longrightarrow}X\sim N({a},{\sigma^2}) f(x)=2πσ1exp[−2σ2(x−a)2],−∞<x<+∞⟹X∼N(a,σ2)
3.3.3.2概率密度曲线及其性质
-
对称轴:均值 x = a x=a x=a
-
∫ − ∞ + ∞ f ( x ) d x = 1 ∫ − ∞ a f ( x ) d x = ∫ a + ∞ f ( x ) d x = 1 2 \int_{-\infty}^{+\infty}f(x)\mathrm{d}x=1\int_{-\infty}^{a}f(x)\mathrm{d}x=\int_{a}^{+\infty}f(x)\mathrm{d}x=\frac12 ∫−∞+∞f(x)dx=1∫−∞af(x)dx=∫a+∞f(x)dx=21
-
均值 α \alpha α反映变量的分布中心, 方差 σ 2 \sigma^{2} σ2反映变量的集中程度;
-
当均值 α = 0 \alpha=0 α=0,方差 σ 2 = 1 \sigma^2=1 σ2=1时,高斯分布为标准正态分布N(0,1)
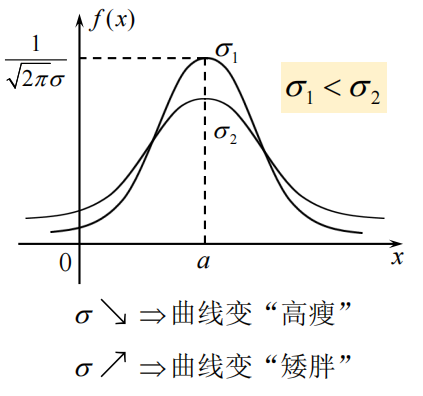
3.3.3.3 高斯变量的标准化/归一化
X ∼ N ( a , σ 2 ) ⟶ Y = X − a σ Y ∼ N ( 0 , 1 ) P ( X ≤ x ) = P ( Y ≤ x − a σ ) X\sim N(a,\sigma^2)\quad \overset{Y=\frac{X-a}\sigma}{\longrightarrow } \quad Y\sim N(0,1)\\P(X\leq x)=P(Y\leq\frac{x-a}\sigma) X∼N(a,σ2)⟶Y=σX−aY∼N(0,1)P(X≤x)=P(Y≤σx−a)
给定任意高斯变量,都可以经过归一化变为标准正态分布Y。
3.3.4 正态分布函数、Q函数、误差函数、互补误差函数
3.3.4.1 正态分布
- 正态分布函数
X ∼ N ( a , σ 2 ) X\sim N(a,\sigma^2) X∼N(a,σ2) F ( x ) = P ( X ≤ x ) = ∫ − ∞ x 1 2 π σ exp ∣ − ( t − a ) 2 2 σ 2 ∣ F( x) = P( X\leq x) = \int _{- \infty}^x\frac 1{\sqrt {2\pi}\sigma}\exp \left | - \frac {\left ( t- a\right ) ^2}{2\sigma^2}\right | F(x)=P(X≤x)=∫−∞x2πσ1exp −2σ2(t−a)2 d t t t
- 标准正态分布函数
F ( x ) = ∫ − ∞ x 1 2 π e − t 2 2 d t F(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}\mathrm{d}t F(x)=∫−∞x2π1e−2t2dt
积分式无闭合形式,只有数值解,需要经过处理以后通过查表求解概率。
3.3.4.2 Q函数
X ∼ N ( 0 , 1 ) X\sim N(0,1) X∼N(0,1)
Q
(
x
)
=
∫
x
+
∞
1
2
π
e
−
t
2
2
d
t
Q(x)=\int_x^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}\mathrm{d}t
Q(x)=∫x+∞2π1e−2t2dt
X
∼
N
(
a
,
σ
2
)
→
Y
=
X
−
a
σ
Y
∼
N
(
0
,
1
)
X\sim N(a,\sigma^2)\quad\xrightarrow{\begin{array}{c}Y=\frac{X-a}\sigma\\\end{array}}\quad Y\sim N(0,1)
X∼N(a,σ2)Y=σX−aY∼N(0,1)
P ( X ≤ x ) = P ( Y ≤ x − a σ ) Q ( x ) = 1 − F ( x − a σ ) P(X\leq x)=P(Y\leq\frac{x-a}{\sigma})\quad\boxed{Q(x)=1-F\left(\frac{x-a}{\sigma}\right)} P(X≤x)=P(Y≤σx−a)Q(x)=1−F(σx−a)
给定任意高斯变量
X
X
X,经过归一化变为标准正态分布
Y
Y
Y后,可以利用Q函数查表求有关的概率。
Q
(
0
)
=
0.5
,
Q
(
x
)
=
1
−
Q
(
−
x
)
Q(0)=0.5,\quad Q(x)=1-Q(-x)
Q(0)=0.5,Q(x)=1−Q(−x)
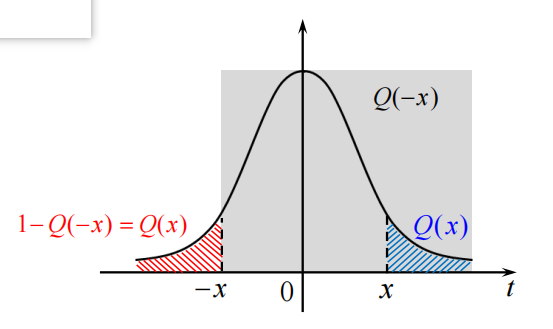
3.4平稳随机过程通过线性系统
随机机过程通过线性系统
只考虑平稳随机过程通过线性时不变系统的情形。
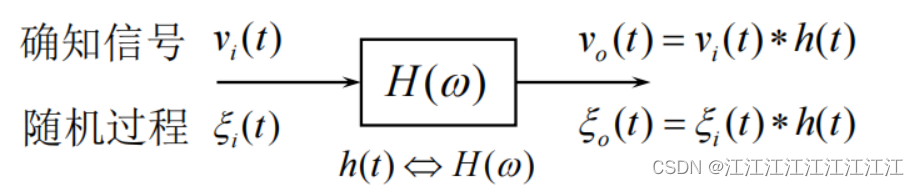
对确知信号(视为随机过程的样本函数):
v
o
(
t
)
=
v
i
(
t
)
∗
h
(
t
)
=
∫
0
+
∞
h
(
τ
)
v
i
(
t
−
τ
)
d
τ
V
o
(
ω
)
V
i
(
ω
)
H
(
ω
)
V
o
(
ω
)
=
V
i
(
ω
)
⋅
H
(
ω
)
\begin{aligned}&v_{o}(t)=v_{i}(t)*h(t)=\int_{0}^{+\infty}h(\tau)v_{i}(t-\tau)\mathrm{d}\tau\\&V_{o}(\omega)\quad V_{i}(\omega)\quad H(\omega)\quad V_{o}(\omega)=V_{i}(\omega)\cdot H(\omega)\end{aligned}
vo(t)=vi(t)∗h(t)=∫0+∞h(τ)vi(t−τ)dτVo(ω)Vi(ω)H(ω)Vo(ω)=Vi(ω)⋅H(ω)
对整个随机过程:
ξ
o
(
t
)
=
ξ
i
(
t
)
∗
h
(
t
)
=
∫
0
+
∞
h
(
τ
)
ξ
i
(
t
−
τ
)
d
τ
\xi_o(t)=\xi_i(t)*h(t)=\int_0^{+\infty}h(\tau)\xi_i(t-\tau)\mathrm{d}\tau
ξo(t)=ξi(t)∗h(t)=∫0+∞h(τ)ξi(t−τ)dτ
3.4.1 随机过程通过线性系统
- 数学期望
E [ ξ i ( t ) ] = a ⟶ E [ ξ o ( t ) ] = a ⋅ H ( 0 ) E\left[\xi_i(t)\right]=a\quad\longrightarrow\quad E\left[\xi_o(t)\right]=a\cdot H(0) E[ξi(t)]=a⟶E[ξo(t)]=a⋅H(0)
输出过程的数学期望为常数,即输入直流分量a与系统直流增益H(0)的乘积。
R
i
(
t
,
t
+
τ
)
=
R
i
(
τ
)
⟶
R
o
(
t
,
t
+
τ
)
=
R
o
(
τ
)
R_i(t,t+\tau)=R_i(\tau)\quad\longrightarrow\quad R_o(t,t+\tau)=R_o(\tau)
Ri(t,t+τ)=Ri(τ)⟶Ro(t,t+τ)=Ro(τ)
输入平稳随机过程,则输出过程自相关函数只与时间间隔有关。
平稳随机过程通过线性系统,输出也是平稳随机过程。
- 证明
E [ ξ o ( t ) ] = a ⋅ H ( 0 ) E[\xi_o(t)]=a\cdot H(0) E[ξo(t)]=a⋅H(0)
E [ ξ o ( t ) ] = E [ ∫ 0 + ∞ h ( τ ) ξ i ( t − τ ) d τ ] = ∫ 0 + ∞ h ( τ ) E [ ξ i ( t − τ ) ] d τ = E [ ξ i ( t ) ] ⋅ ∫ 0 + ∞ h ( τ ) d τ = a ⋅ ∫ 0 + ∞ h ( τ ) d τ ⟶ E [ ξ o ( t ) ] = a ⋅ H ( 0 ) \begin{aligned} E[\xi_{o}(t)]& =E\bigg[\int_{0}^{+\infty}h(\tau)\xi_{i}(t-\tau)\mathrm{d}\tau\bigg]= \int_{0}^{+\infty}h(\tau)E\bigg[\xi_{i}(t-\tau)\bigg]\mathrm{d}\tau \\ &=E\left[\xi_i(t)\right]\cdot\int_0^{+\infty}h(\tau)\mathrm{d}\tau \\ &=a\cdot\int_0^{+\infty}h(\tau)\mathrm{d}\tau\quad\longrightarrow\quad E\left[\xi_o(t)\right]=a\cdot H(0) \end{aligned} E[ξo(t)]=E[∫0+∞h(τ)ξi(t−τ)dτ]=∫0+∞h(τ)E[ξi(t−τ)]dτ=E[ξi(t)]⋅∫0+∞h(τ)dτ=a⋅∫0+∞h(τ)dτ⟶E[ξo(t)]=a⋅H(0)
H ( f ) = ∫ 0 + ∞ h ( τ ) e − j 2 π f τ d τ H ( 0 ) = ∫ 0 + ∞ h ( τ ) e − j 2 π f τ ⏟ 1 d τ ∣ f = 0 = ∫ 0 + ∞ h ( τ ) d τ \begin{aligned}&H(f)=\int_{0}^{+\infty}h(\tau)e^{-j2\pi f\tau}\mathrm{d}\tau\\&H(0)=\int_{0}^{+\infty}h(\tau)\underbrace{e^{-j2\pi f\tau}}_{1}\mathrm{d}\tau\Bigg|_{f=0}=\int_{0}^{+\infty}h(\tau)\mathrm{d}\tau\end{aligned} H(f)=∫0+∞h(τ)e−j2πfτdτH(0)=∫0+∞h(τ)1 e−j2πfτdτ f=0=∫0+∞h(τ)dτ
- 证明
R o ( t , t + τ ) = R o ( τ ) R_o(t,t+\tau)=R_o(\tau) Ro(t,t+τ)=Ro(τ)
R o ( t , t + τ ) = E [ ξ o ( t ) ξ o ( t + τ ) ] = E [ ∫ 0 + ∞ h ( α ) ξ i ( t − α ) d α ∫ 0 + ∞ h ( β ) ξ i ( t + τ − β ) d β ] = ∫ 0 + ∞ ∫ 0 + ∞ h ( α ) h ( β ) E [ ξ i ( t − α ) ξ i ( t + τ − β ) ] d α d β \begin{aligned} R_{o}(t,t+\tau)& =E\Big[\xi_{o}(t)\xi_{o}(t+\tau)\Big] \\ &=E\left[\int_0^{+\infty}h(\alpha)\xi_i(t-\alpha)\mathrm{d}\alpha\int_0^{+\infty}h(\beta)\xi_i(t+\tau-\beta)\mathrm{d}\beta\right] \\ &=\int_{0}^{+\infty}\int_{0}^{+\infty}h(\alpha)h(\beta)E\Big[\xi_{i}(t-\alpha)\xi_{i}(t+\tau-\beta)\Big]\mathrm{d}\alpha\mathrm{d}\beta \end{aligned} Ro(t,t+τ)=E[ξo(t)ξo(t+τ)]=E[∫0+∞h(α)ξi(t−α)dα∫0+∞h(β)ξi(t+τ−β)dβ]=∫0+∞∫0+∞h(α)h(β)E[ξi(t−α)ξi(t+τ−β)]dαdβ
E [ ξ i ( t − α ) ξ i ( t + τ − β ) ] = R i ( τ + α − β ) R o ( t , t + τ ) = ∫ 0 + ∞ ∫ 0 + ∞ h ( α ) h ( β ) R i ( τ + α − β ) d α d β = R o ( τ ) \begin{aligned} &E\Big[\xi_{i}(t-\alpha)\xi_{i}(t+\tau-\beta)\Big]=R_{i}(\tau+\alpha-\beta) \\ &R_{o}(t,t+\tau)=\int_{0}^{+\infty}\int_{0}^{+\infty}h(\alpha)h(\beta)R_{i}(\tau+\alpha-\beta)\mathrm{d}\alpha\mathrm{d}\beta=R_{o}(\tau) \end{aligned} E[ξi(t−α)ξi(t+τ−β)]=Ri(τ+α−β)Ro(t,t+τ)=∫0+∞∫0+∞h(α)h(β)Ri(τ+α−β)dαdβ=Ro(τ)
因此输出过程自相关函数只依赖时间间隔,而与时间起点无关。
- 功率谱密度
P i ( ω ) ⟹ P 0 ( ω ) = P i ( ω ) ∣ H ( ω ) ∣ 2 P_i(\omega)\quad\Longrightarrow\quad P_0(\omega)=P_i(\omega)\left|H(\omega)\right|^2 Pi(ω)⟹P0(ω)=Pi(ω)∣H(ω)∣2
输出过程的功率谱为输入功率谱 P i ( ω ) P_i(\omega) Pi(ω)与系统功率增益 ∣ H ( ω ) ∣ 2 \left|H(\omega)\right|^2 ∣H(ω)∣2的乘积。
研究一般随机过程经过线性系统的输出较复杂,但特殊地,线性系统输入高斯过程,则输出也为高斯过程,但数字特征会发生改变。
- 随机过程通过线性系统
P 0 ( ω ) = P i ( ω ) ∣ H ( ω ) ∣ 2 P_0(\omega)=P_i(\omega){\left|H(\omega)\right|}^2 P0(ω)=Pi(ω)∣H(ω)∣2
R o ( t , t + τ ) = ∫ 0 + ∞ ∫ 0 + ∞ h ( α ) h ( β ) R i ( τ + α − β ) d α d β R_o(t,t+\tau)=\int_0^{+\infty}\int_0^{+\infty}h(\alpha)h(\beta)R_i(\tau+\alpha-\beta)\mathrm{d}\alpha\mathrm{d}\beta Ro(t,t+τ)=∫0+∞∫0+∞h(α)h(β)Ri(τ+α−β)dαdβ
P o ( ω ) = ∫ − ∞ + ∞ R o ( τ ) e − j ω τ d τ = ∫ − ∞ + ∞ ∫ 0 + ∞ ∫ 0 + ∞ [ h ( α ) h ( β ) R i ( τ + α − β ‾ ) d α d β ] e − j ω τ d τ τ ′ = τ + α − β τ = τ ′ − α + β , d τ = d τ ′ = ∫ 0 + ∞ h ( α ) e j ω α ‾ d α ⋅ ∫ 0 + ∞ h ( β ) e − j ω β d β ⋅ ∫ − ∞ + ∞ R i ( τ ′ ) e − j ω τ ′ d τ ′ = H ∗ ( ω ) ⋅ H ( ω ) ⋅ P i ( ω ) = P i ( ω ) ∣ H ( ω ) ∣ 2 \begin{aligned} P_{o}(\omega)& =\int_{-\infty}^{+\infty}R_{o}(\tau)e^{-j\omega\tau}\mathrm{d}\tau \\ &=\int_{-\infty}^{+\infty}\int_{0}^{+\infty}\int_{0}^{+\infty}\left[h(\alpha)h(\beta)R_{i}(\underline{\tau+\alpha-\beta})\mathrm{d}\alpha\mathrm{d}\beta\right]e^{-j\omega\tau}\mathrm{d}\tau \\ &\tau^{\prime}=\tau+\alpha-\beta\quad\tau=\tau^{\prime}-\alpha+\beta,\mathrm{d}\tau=\mathrm{d}\tau^{\prime} \\ &=\int_{0}^{+\infty}h(\alpha)e^{\underline{j\omega\alpha}}\mathrm{d}\alpha\cdot\int_{0}^{+\infty}h(\beta)e^{-j\omega\beta}\mathrm{d}\beta\cdot\int_{-\infty}^{+\infty}R_{i}(\tau^{\prime})e^{-j\omega\tau^{\prime}}\mathrm{d}\tau^{\prime} \\ &=H^{*}(\omega)\cdot H(\omega)\cdot P_{i}(\omega)=P_{i}(\omega)\big|H(\omega)\big|^{2} \end{aligned} Po(ω)=∫−∞+∞Ro(τ)e−jωτdτ=∫−∞+∞∫0+∞∫0+∞[h(α)h(β)Ri(τ+α−β)dαdβ]e−jωτdττ′=τ+α−βτ=τ′−α+β,dτ=dτ′=∫0+∞h(α)ejωαdα⋅∫0+∞h(β)e−jωβdβ⋅∫−∞+∞Ri(τ′)e−jωτ′dτ′=H∗(ω)⋅H(ω)⋅Pi(ω)=Pi(ω) H(ω) 2

3.5窄带随机过程
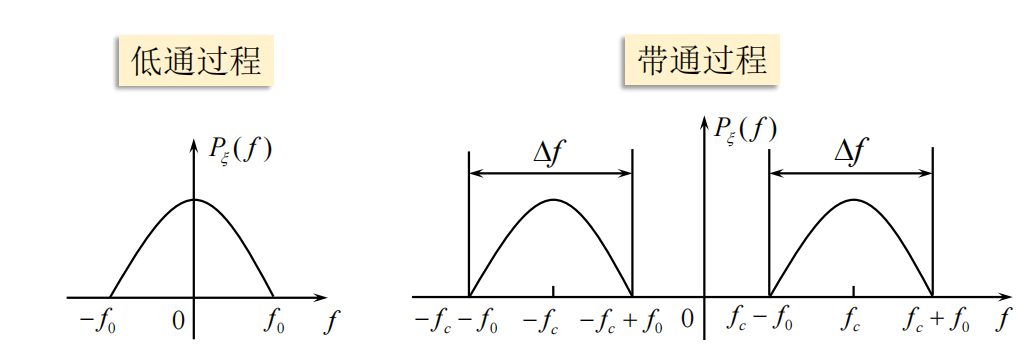
P
ξ
(
f
)
=
{
P
ξ
(
f
)
∣
f
∣
≤
f
0
0
∣
f
∣
>
f
0
P
ξ
(
f
)
=
{
P
ξ
(
f
)
f
c
−
f
0
≤
∣
f
∣
≤
f
c
+
f
0
0
其他
P_\xi(f)=\begin{cases}P_\xi(f)&\left|f\right|\leq f_0\\\\0&\left|f\right|>f_0\end{cases}\quad \quad\quad P_\xi(f)=\begin{cases}P_\xi(f)&f_c-f_0\leq\left|f\right|\leq f_c+f_0\\\\0&\text{其他}\end{cases}
Pξ(f)=⎩
⎨
⎧Pξ(f)0∣f∣≤f0∣f∣>f0Pξ(f)=⎩
⎨
⎧Pξ(f)0fc−f0≤∣f∣≤fc+f0其他
3.5.1 窄带随机过程的定义
通带宽度: Δ f ≪ f c \Delta f\ll f_c Δf≪fc, 且中心频率 f c f_c fc 远离零频率的系统。
窄带过程:随机过程通过以 f c f_c fc为中心频率的窄带系统的输出过程。
- 窄带过程时、频示意图
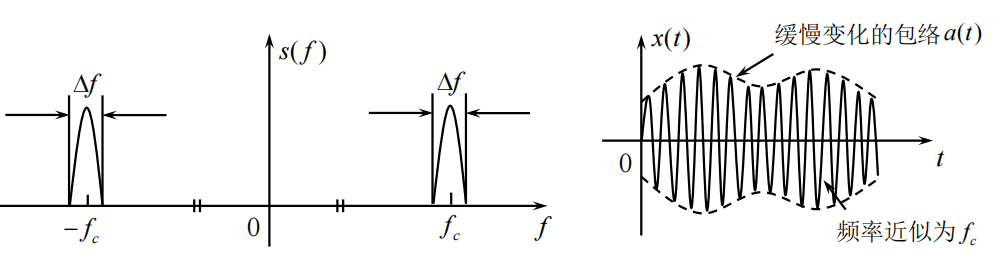
窄带随机过程的数学表示
ξ
(
t
)
=
a
ξ
(
t
)
‾
cos
[
ω
c
t
+
φ
ξ
(
t
)
‾
]
\xi(t)=\underline{a_\xi(t)}\cos\left[\omega_ct+\underline{\varphi_\xi(t)}\right]
ξ(t)=aξ(t)cos[ωct+φξ(t)]
a
ξ
(
t
)
{a_\xi(t)}
aξ(t):随机包络
φ ξ ( t ) {\varphi_\xi(t)} φξ(t):随机相位
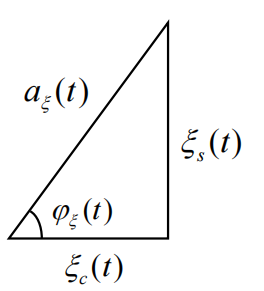
- 同相分量-正交分量表达式
ξ ( t ) = a ξ ( t ) cos [ ω c t + φ ξ ( t ) ] = a ξ ( t ) cos φ ξ ( t ) ‾ cos ω c t − a ξ ( t ) sin φ ξ ( t ) ‾ sin ω c t = ξ c ( t ) ‾ cos ω c t − ξ s ( t ) ‾ sin ω c t \begin{aligned} \xi(t)& =a_{\xi}(t)\cos\Bigl[\omega_{c}t+\varphi_{\xi}(t)\Bigr] \\ &=\underline{a_\xi(t)\cos\varphi_\xi(t)}\cos\omega_ct-\underline{a_\xi(t)\sin\varphi_\xi(t)}\sin\omega_ct \\ &=\underline{\xi_c(t)}\cos\omega_ct-\underline{\xi_s(t)}\sin\omega_ct \end{aligned} ξ(t)=aξ(t)cos[ωct+φξ(t)]=aξ(t)cosφξ(t)cosωct−aξ(t)sinφξ(t)sinωct=ξc(t)cosωct−ξs(t)sinωct
同相分量: ξ c ( t ) = a ξ ( t ) cos φ ξ ( t ) \xi_c(t)=a_\xi(t)\cos\varphi_\xi(t) ξc(t)=aξ(t)cosφξ(t)
正交分量:
ξ
s
(
t
)
=
a
ξ
(
t
)
sin
φ
ξ
(
t
)
\xi_s(t)=a_\xi(t)\sin\varphi_\xi(t)
ξs(t)=aξ(t)sinφξ(t)
{
a
ξ
(
t
)
=
ξ
c
2
(
t
)
+
ξ
s
2
(
t
)
φ
ξ
(
t
)
=
arctan
ξ
s
(
t
)
ξ
c
(
t
)
\begin{cases}a_\xi(t)=\sqrt{\xi_c^2(t)+\xi_s^2(t)}\\\varphi_\xi(t)=\arctan\frac{\xi_s(t)}{\xi_c(t)}\end{cases}
{aξ(t)=ξc2(t)+ξs2(t)φξ(t)=arctanξc(t)ξs(t)
3.5.2 ξ c ( t ) 和 ξ s ( t ) \xi_{c}(t)\text{和}\xi_{s}(t) ξc(t)和ξs(t)的统计特性
ξ ( t ) \xi(t) ξ(t) 为平稳高斯窄带过程,均值为0,方差为 σ ξ 2 \sigma_\mathrm{\xi}^2 σξ2。
ξ ( t ) = ξ c ( t ) cos ω c t − ξ s ( t ) sin ω c t \xi(t)=\xi_c(t)\cos\omega_ct-\xi_s(t)\sin\omega_ct ξ(t)=ξc(t)cosωct−ξs(t)sinωct
ξ c ( t ) \xi_c(t) ξc(t)和 ξ s ( t ) \xi_s(t) ξs(t) 的数学期望均为0;
E [ ξ c ( t ) ] = E [ ξ s ( t ) ] = 0 E[\xi_c(t)]=E[\xi_s(t)]=0 E[ξc(t)]=E[ξs(t)]=0 ξ c ( t ) \xi_c(t) ξc(t) 和 ξ s ( t ) \xi_s(t) ξs(t)的相关函数均只与时间间隔有关,故必然平稳;
ξ c ( t ) \xi_c(t) ξc(t)和 ξ s ( t ) \xi_s(t) ξs(t)的自相关函数相同;
ξ c ( t ) \xi_c(t) ξc(t) 和 ξ s ( t ) \xi_s(t) ξs(t) 的方差相同; σ ξ 2 = σ c 2 = σ s 2 \sigma_\xi^2=\sigma_c^2=\sigma_s^2 σξ2=σc2=σs2
ξ c ( t ) \xi_c(t) ξc(t) 和 ξ s ( t ) \xi_s(t) ξs(t)为互不相关、统计独立的高斯变量。
ξ c ( t ) 和 ξ s ( t ) 为零均值,等方差,不相关,独立的平稳高斯过程。 \xi_c(t)\text{和 }\xi_s(t)\text{为零均值,等方差,不相关,独立的平稳高斯过程。} ξc(t)和 ξs(t)为零均值,等方差,不相关,独立的平稳高斯过程。
3.5.3 a ξ ( t ) 和 φ ξ ( t ) 的统计特性 a_\xi(t)\text{ 和 }\varphi_\xi(t)\text{的统计特性} aξ(t) 和 φξ(t)的统计特性的统计特性
- 瑞利分布
f ( a ξ ) = a ξ σ ξ 2 e x p ( − a ξ 2 2 σ ξ 2 ) , a ξ ≥ 0 f(a_\xi)=\frac{a_\xi}{\sigma_\xi^2}\mathrm{exp}\biggl(-\frac{a_\xi^2}{2\sigma_\xi^2}\biggr),a_\xi\geq0 f(aξ)=σξ2aξexp(−2σξ2aξ2),aξ≥0
- 均匀分布
f ( φ ξ ) = 1 2 π , 0 ≤ φ ξ ≤ 2 π f(\varphi_\xi)=\frac1{2\pi},0\leq\varphi_\xi\leq2\pi f(φξ)=2π1,0≤φξ≤2π
- 随机相位和随机包络统计独立
f ( a ξ , φ ξ ) = f ( a ξ ) ⋅ f ( φ ξ ) f(a_\xi,\varphi_\xi)=f(a_\xi)\cdot f(\varphi_\xi) f(aξ,φξ)=f(aξ)⋅f(φξ)
3.6正弦波加窄带高斯噪声
3.6.1 数学模型
- 信号模型
r ( t ) = A cos ( ω c t + θ ‾ ) + n ( t ) ‾ r(t)=A\cos(\omega_ct+\underline{\theta})+\underline{n(t)} r(t)=Acos(ωct+θ)+n(t)
θ \theta θ:随机相位
n ( t ) {n(t)} n(t):均值为0,方差为c的窄带高斯噪声
- 同相分量-正交分量表达式
n ( t ) = n c ( t ) cos ω c t − n s ( t ) sin ω c t r ( t ) = A cos ( ω c t + θ ) + n c ( t ) cos ω c t − n s ( t ) sin ω c t = [ A cos θ + n c ( t ) ] ‾ cos ω c t − [ A sin θ + n s ( t ) ] ‾ sin ω c t = z c ( t ) ‾ cos ω c t − z s ( t ) ‾ sin ω c t \begin{aligned} &n(t) =n_c(t)\cos\omega_ct-n_s(t)\sin\omega_ct \\ &r(t) =A\cos(\omega_ct+\theta)+n_c(t)\cos\omega_ct-n_s(t)\sin\omega_ct \\ &=\underline{\begin{bmatrix}A\cos\theta+n_c(t)\end{bmatrix}}\cos\omega_ct-\underline{\begin{bmatrix}A\sin\theta+n_s(t)\end{bmatrix}}\sin\omega_ct \\ &=\underline{z_c(t)}\cos\omega_ct-\underline{z_s(t)}\sin\omega_ct \end{aligned} n(t)=nc(t)cosωct−ns(t)sinωctr(t)=Acos(ωct+θ)+nc(t)cosωct−ns(t)sinωct=[Acosθ+nc(t)]cosωct−[Asinθ+ns(t)]sinωct=zc(t)cosωct−zs(t)sinωct
同相分量: z c ( t ) = A cos θ + n c ( t ) z_c(t)=A\cos\theta+n_c(t) zc(t)=Acosθ+nc(t)
正交分量: z s ( t ) = A sin θ + n s ( t ) z_s(t)=A\sin\theta+n_s(t) zs(t)=Asinθ+ns(t)
- 幅度-相位表达式
r ( t ) = z c ( t ) cos ω c t − z s ( t ) sin ω c t = z ( t ) ‾ cos [ ω c t + φ ( t ) ‾ ] r(t)=z_c(t)\cos\omega_ct-z_s(t)\sin\omega_ct=\underline{z(t)}\cos{}[ \omega_ct+\underline{\varphi(t)} ] r(t)=zc(t)cosωct−zs(t)sinωct=z(t)cos[ωct+φ(t)]
随机包络 z ( t ) = z c 2 ( t ) + z s 2 ( t ) \text{随机包络}\quad z(t)=\sqrt{z_c^2(t)+z_s^2(t)}\quad 随机包络z(t)=zc2(t)+zs2(t)
随机相位 φ ( t ) = arctan z s ( t ) z c ( t ) \text{随机相位}\quad\varphi(t)=\arctan\frac{z_s(t)}{z_c(t)} 随机相位φ(t)=arctanzc(t)zs(t)
- 同相分量-正交分量与幅度-相位的关系
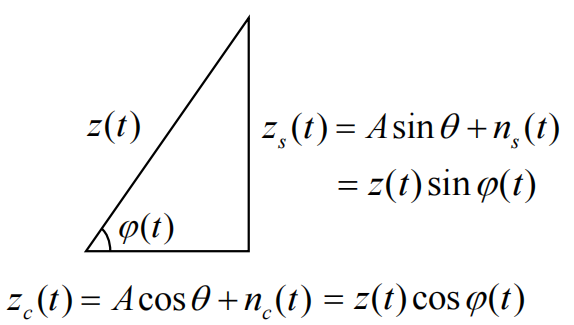
3.6.2 同相分量和正交分量和统计特性
z c ( t ) = A cos θ + n c ( t ) z_c(t)=A\cos\theta+\boxed{n_c(t)} zc(t)=Acosθ+nc(t)
z s ( t ) = A sin θ + n s ( t ) z_s(t)=A\sin\theta+\boxed{n_s(t)} zs(t)=Asinθ+ns(t)
高斯窄带过程的同相分量与正交分量零均值,方差相同的高斯变量
随机相位
θ
\theta
θ给定时,$z_c( t) $ 和 $z_s( t) $为取值不相关,相互独立,且 同分布的高斯变量,其数字特征为:
{
E
[
z
c
(
t
)
]
=
A
cos
θ
E
[
z
s
(
t
)
]
=
A
sin
θ
σ
n
2
=
σ
c
2
=
σ
s
2
\begin{cases}E[z_c(t)]=A\cos\theta\\E[z_s(t)]=A\sin\theta\\\sigma_n^2=\sigma_c^2=\sigma_s^2\end{cases}
⎩
⎨
⎧E[zc(t)]=AcosθE[zs(t)]=Asinθσn2=σc2=σs2
3.6.3 随机包络和随机相位的统计特性
随机包络 z ( t ) 的统计特性 \text{随机包络}z(t)\text{的统计特性} 随机包络z(t)的统计特性
莱斯分布/广义瑞利分布
f
(
z
)
=
z
σ
n
2
exp
(
−
z
2
+
A
2
2
σ
n
2
)
I
0
(
A
z
σ
n
2
)
,
z
≥
0
f(z)=\frac{z}{\sigma_n^2}\exp\biggl(-\frac{z^2+A^2}{2\sigma_n^2}\biggr)I_0\biggl(\frac{Az}{\sigma_n^2}\biggr),z\geq0
f(z)=σn2zexp(−2σn2z2+A2)I0(σn2Az),z≥0
I
0
(
x
)
=
1
2
π
∫
0
2
π
exp
[
x
cos
φ
]
d
φ
第一类零阶修正贝塞尔函数
I_0(x)=\frac1{2\pi}\int_0^{2\pi}\exp[x\cos\varphi]\mathrm{d}\varphi\quad\text{第一类零阶修正贝塞尔函数}
I0(x)=2π1∫02πexp[xcosφ]dφ第一类零阶修正贝塞尔函数
大信噪比环境:
r
=
A
2
2
σ
2
≫
1
r=\frac{A^2}{2\sigma^2}\gg1
r=2σ2A2≫1 近似为高斯分布
小信噪比环境: A → 0 A\to0 A→0 退化为瑞利分布
随机相位 φ ( t ) \varphi(t) φ(t)的概率密度 f ( φ ) f(\varphi) f(φ)与信噪比环境有关。
- 小信噪比环境: f ( φ ) f(\varphi) f(φ) 服从均匀分布
- 大信噪比环境:集中在有用信号相位附近,在0相位附近取值集中。
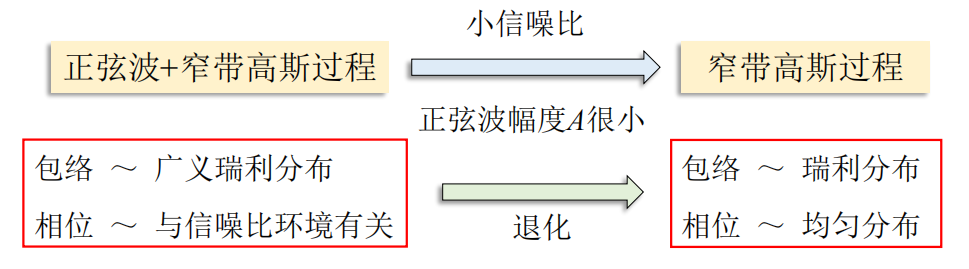
f
(
a
ξ
)
=
a
ξ
σ
ξ
2
exp
(
−
a
ξ
2
2
σ
ξ
2
)
,
a
ξ
≥
0
f(a_\xi)=\frac{a_\xi}{\sigma_\xi^2}\exp\biggl(-\frac{a_\xi^2}{2\sigma_\xi^2}\biggr),a_\xi\geq0
f(aξ)=σξ2aξexp(−2σξ2aξ2),aξ≥0
退化后
f
(
z
)
=
z
σ
n
2
exp
(
−
z
2
+
A
2
2
σ
n
2
)
I
0
(
A
z
σ
n
2
)
,
z
≥
0
f
(
φ
ξ
)
=
1
2
π
,
0
≤
φ
ξ
≤
2
π
f(z)=\frac{z}{\sigma_{n}^{2}}\exp\biggl(-\frac{z^{2}+A^{2}}{2\sigma_{n}^{2}}\biggr)I_{0}\biggl(\frac{Az}{\sigma_{n}^{2}}\biggr),z\geq0\\f(\varphi_{\xi})=\frac{1}{2\pi},0\leq\varphi_{\xi}\leq2\pi
f(z)=σn2zexp(−2σn2z2+A2)I0(σn2Az),z≥0f(φξ)=2π1,0≤φξ≤2π
窄带过程”和“正弦波+高斯窄带过程”两类模型的有关结论常用于分析系统抗噪声性能。
结合误差函数、互补误差函数的定义可以求解系统的总误码率。
3.7高斯白噪声和带限白噪声
3.7.1 高斯白噪声
- 白噪声
功率谱密度均匀分布在整个频率范围内的随机过程称为白噪声。
- 功率谱密度
P n ( ω ) = n 0 2 , − ∞ < ω < + ∞ P n ( ω ) = n 0 , ω ≥ 0 P_n(\omega)=\frac{n_0}2,-\infty<\omega<+\infty\qquad P_n(\omega)=n_0,\omega\geq0 Pn(ω)=2n0,−∞<ω<+∞Pn(ω)=n0,ω≥0
n 0 : n_0\colon n0: 单边噪声功率谱密度
n 0 2 : \frac{n_0}2: 2n0: 双边噪声功率谱密度 2
- 自相关函数
P n ( ω ) = n 0 2 , − ∞ < ω < + ∞ ⟺ R ( τ ) = n 0 2 δ ( τ ) P_{n}(\omega)=\frac{n_{0}}{2},-\infty<\omega<+\infty\quad\Longleftrightarrow\quad R(\tau)=\frac{n_{0}}{2}\delta(\tau) Pn(ω)=2n0,−∞<ω<+∞⟺R(τ)=2n0δ(τ)
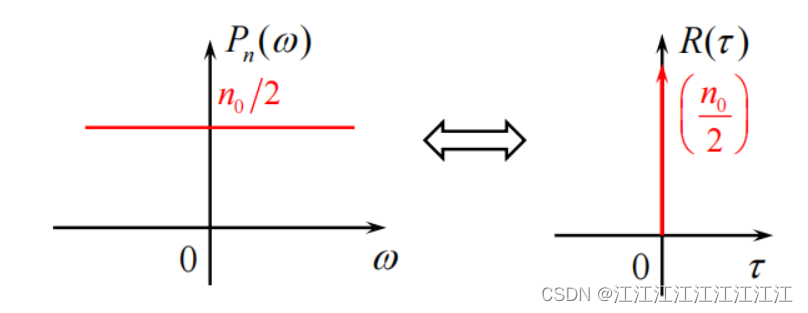
白噪声在任意两个不同时刻上取值互不相关,只有在间隔 τ = 0 \tau=0 τ=0 时才相关。
- 高斯白噪声
服从高斯分布的白噪声称为高斯白噪声。
- 性质
高斯白噪声的特点是:在任意两个不同时刻上随机变量互不相关且统计独立
- 实际应用
实际中不存在理想白噪声,因为其功率为无穷大,若噪声功率谱均匀分布的频率范围远大于通信系统的工作频带,则视为白噪声。
3.7.2 低通白噪声
- 功率谱密度和自相关函数
P
n
(
ω
)
=
{
n
0
2
∣
ω
∣
≤
ω
H
0
∣
ω
∣
>
ω
H
⟶
R
(
τ
)
=
n
0
f
H
sin
ω
H
τ
ω
H
τ
P_n(\omega)=\begin{cases}\frac{n_0}{2}&\left|\omega\right|\leq\omega_H\\\\0&\left|\omega\right|>\omega_H\end{cases}\quad{\longrightarrow}\quad R(\tau)=n_0f_H\frac{\sin\omega_H\tau}{\omega_H\tau}
Pn(ω)=⎩
⎨
⎧2n00∣ω∣≤ωH∣ω∣>ωH⟶R(τ)=n0fHωHτsinωHτ

- 平均功率
S = R ( 0 ) = n 0 f H S = ∫ − ∞ + ∞ P n ( f ) d f = 1 2 π ∫ − ∞ + ∞ P n ( ω ) d ω = 1 2 π ∫ − ω H ω H n 0 2 d ω = n 0 f H \begin{aligned}&S=R(0)=n_0f_H\\&S=\int_{-\infty}^{+\infty}P_n(f)\mathrm{d}f=\frac1{2\pi}\int_{-\infty}^{+\infty}P_n(\omega)\mathrm{d}\omega\\&=\frac1{2\pi}\int_{-\omega_H}^{\omega_H}\frac{n_0}2\mathrm{d}\omega=n_0f_H\end{aligned} S=R(0)=n0fHS=∫−∞+∞Pn(f)df=2π1∫−∞+∞Pn(ω)dω=2π1∫−ωHωH2n0dω=n0fH
对低通白噪声按照抽样定理抽样时,各抽样值为互不相关的随机变量。
3.7.3 带通白噪声
- 功率谱密度和自相关函数
P n ( f ) = { n 0 2 f c − B 2 ≤ ∣ f ∣ ≤ f c + B 2 0 其他 ⟺ R ( τ ) = n 0 B S a ( π B τ ) cos 2 π f c τ P_n(f)=\begin{cases}\frac{n_0}{2}&f_c-\frac{B}{2}\leq\left|f\right|\leq f_c+\frac{B}{2}\\0&\text{其他}\end{cases}\Longleftrightarrow\quad R(\tau)=n_0BSa(\pi B\tau)\cos2\pi f_c\tau Pn(f)={2n00fc−2B≤∣f∣≤fc+2B其他⟺R(τ)=n0BSa(πBτ)cos2πfcτ
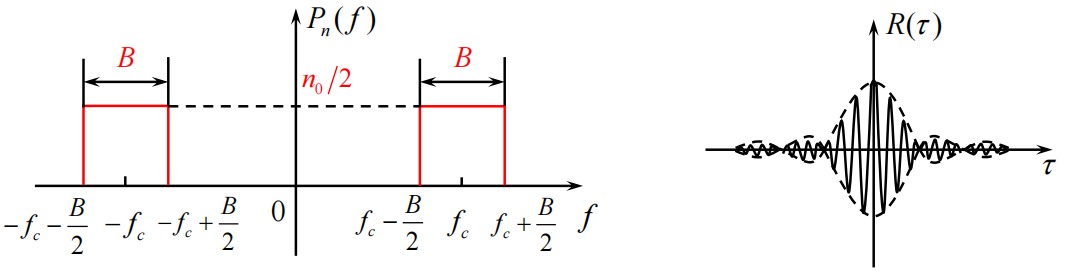
- 平均功率
S = R ( 0 ) = n 0 B S = ∫ − ∞ + ∞ P n ( f ) d f = 2 B ⋅ n 0 2 = n 0 B \begin{aligned}&S=R(0)=n_0B\\&S=\int_{-\infty}^{+\infty}P_{n}(f)\mathrm{d}f=2B\cdot\frac{n_{0}}{2}=n_{0}B\end{aligned} S=R(0)=n0BS=∫−∞+∞Pn(f)df=2B⋅2n0=n0B
- 低通白噪声
P n ( ω ) = { n 0 2 ∣ ω ∣ ≤ ω H 0 ∣ ω ∣ > ω H ⟺ R ( τ ) = n 0 f H sin ω H τ ω H τ P_n(\omega)=\begin{cases}\frac{n_0}{2}&\left|\omega\right|\leq\omega_H\\0&\left|\omega\right|>\omega_H\end{cases}\quad\Longleftrightarrow\quad R(\tau)=n_0f_H\frac{\sin\omega_H\tau}{\omega_H\tau} Pn(ω)={2n00∣ω∣≤ωH∣ω∣>ωH⟺R(τ)=n0fHωHτsinωHτ
- 带通白噪声
P n ( f ) = { n 0 2 f c − B 2 ≤ ∣ f ∣ ≤ f c + B 2 0 其他 ⟺ R ( τ ) = n 0 B S a ( π B τ ) cos 2 π f c τ P_n(f)=\begin{cases}\frac{n_0}{2}&f_c-\frac{B}{2}\leq\left|f\right|\leq f_c+\frac{B}{2}\\0&\text{其他}\end{cases}\quad\Longleftrightarrow\quad R(\tau)=n_0BSa(\pi B\tau)\cos2\pi f_c\tau Pn(f)={2n00fc−2B≤∣f∣≤fc+2B其他⟺R(τ)=n0BSa(πBτ)cos2πfcτ