使用背景

当我们需要把图像进行放大或者缩小的时候，第一反应是使用resize()实现。很多情况下，我们会调用最近邻插值和双线性插值去放大图片，当然要说没有分辨率的损失那是不可能的，只能说在放大图片的过程中尽可能增加了图片的分辨率。这里介绍这两种放大图片尺寸的方法代码，并说明其中优缺点同时看效果，最后再做一个对比和总结。

- 最近邻插值方法

- 双线性插值方法

- 总结

为了更好的展现出插值方法的效果，先利用切边操作把图片设置为（350，350）大小，再各利用插值法把图片的height和weigth各扩大一倍为（700，700），之后比较原始图片和使用了插值方法图片的分辨率或者说清晰度。切片值设置因图而异。代码如下。

img=cv2.imread(r'C:\Users\ZFG\PycharmProjects\Lenet_test\orinal.jpg')
print(img.shape[:2])  #输出为(1491, 1080)
img=img[650:1000,200:550]
print(img.shape[:2])  #输出为(350, 350)
cv2.imwrite(r'C:\Users\ZFG\PycharmProjects\Lenet_test\test.jpg',img) #保存图片在命名为test
cv2.imshow('orinal',img)
cv2.waitKey(0)

最近邻插值方法

代码如下所示可以实现：

import numpy as np
import cv2

def function(img):
    height,width,channels=img.shape #获得高宽三颜色通道三个值
    empty=np.zeros((700,700,channels),np.uint8)  #设置一个（700，700）大小的三维0数组
    sh=700/height
    sw=700/width
    for i in range(700):
        for j in range(700):
            x=int(i/sh)
            y=int(j/sw)
            empty[i,j]=img[x,y]
    return empty

img=cv2.imread(r'C:\Users\ZFG\PycharmProjects\Lenet_test\test.jpg')
cv2.imshow('origin',img)
zoom=function(img)
cv2.imshow('bigger1',zoom)
cv2.waitKey(0)

最后结果如下图所示：

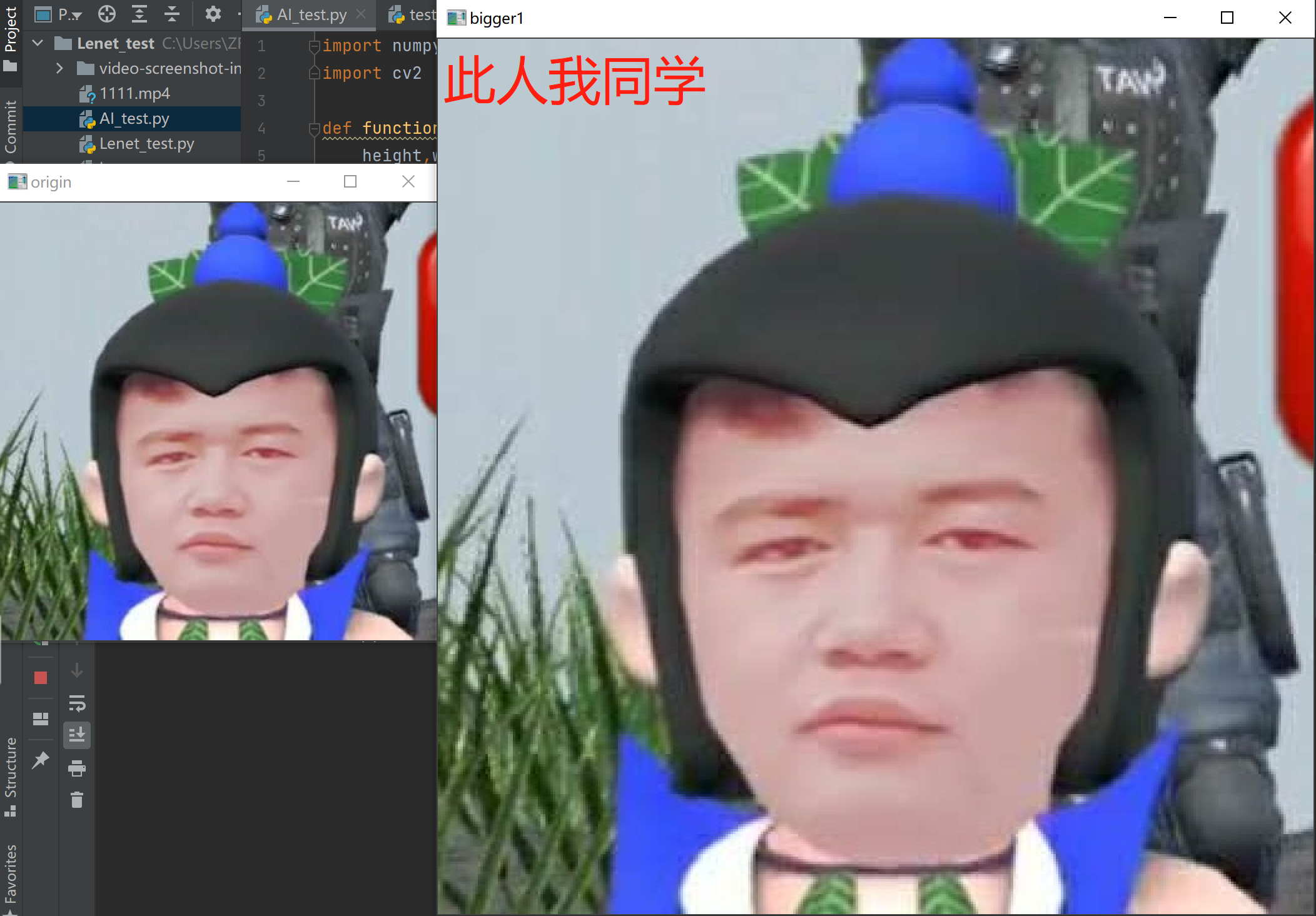
结论：

• 优点：算法容易实现，时空复杂度较小，运行较快
• 缺点：放大后轮廓锯齿状较多，效果一般

双线性插值方法

代码如下所示可以实现：

import numpy as np
import cv2

def bilinear_interpolation(img,out):  #out为希望输出大小
    src_h, src_w, channel = img.shape  #获取三通道
    dst_h, dst_w = out[1], out[0]
    if src_h == dst_h and src_w == dst_w:
        return img.copy()
    dst_img = np.zeros((dst_h,dst_w,3),dtype=np.uint8)
    scale_x, scale_y = float(src_w) / dst_w, float(src_h) / dst_h
    for i in range(3):
        for dst_y in range(dst_h):
            for dst_x in range(dst_w):
 
                # find the origin x and y coordinates of dst image x and y
                # use geometric center symmetry
                # if use direct way, src_x = dst_x * scale_x
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
 
                # find the coordinates of the points which will be used to compute the interpolation
                src_x0 = int(np.floor(src_x))
                src_x1 = min(src_x0 + 1 ,src_w - 1)
                src_y0 = int(np.floor(src_y))
                src_y1 = min(src_y0 + 1, src_h - 1)
 
                # calculate the interpolation
                temp0 = (src_x1 - src_x) * img[src_y0,src_x0,i] + (src_x - src_x0) * img[src_y0,src_x1,i]
                temp1 = (src_x1 - src_x) * img[src_y1,src_x0,i] + (src_x - src_x0) * img[src_y1,src_x1,i]
                dst_img[dst_y,dst_x,i] = int((src_y1 - src_y) * temp0 + (src_y - src_y0) * temp1)
 
    return dst_img
 
 
if __name__ == '__main__':
    img = cv2.imread(r'C:\Users\ZFG\PycharmProjects\Lenet_test\test.jpg')
    cv2.imshow('orinal',img)
    dst = bilinear_interpolation(img,(700,700))
    cv2.imshow('test',dst)
    cv2.waitKey()

最后结果如下图所示：

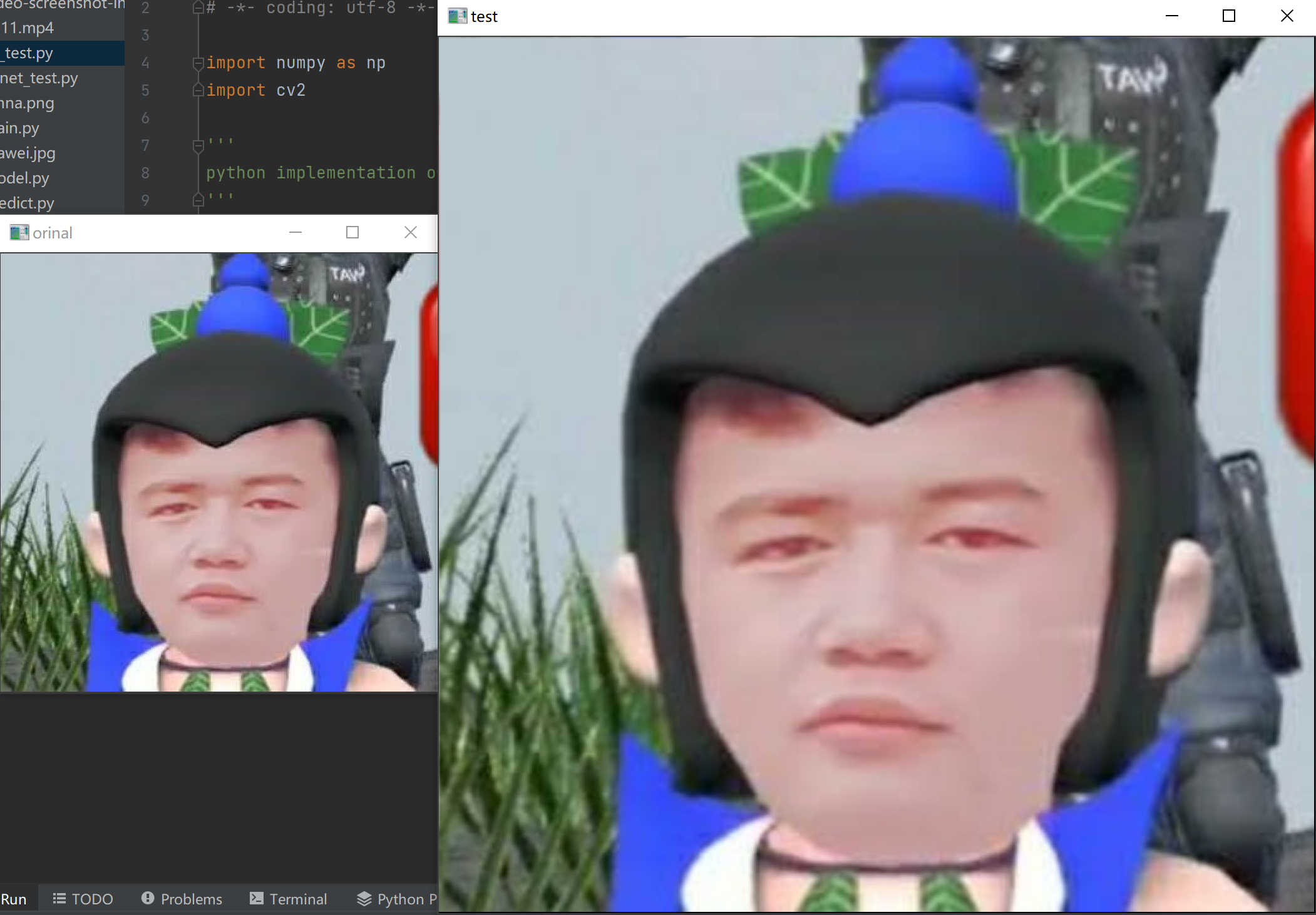
结论：

• 优点：图像几乎不失真，放大后分辨率也非常高
• 缺点：算法不易实现，时空复杂度大，运行很慢，对CPU要求较高，大批处理耗费算力大

总结

在实际操作中，选用最近邻插值方法和双线性插值方法的时候，不需要这么多源码实现，只需要在resize()的时候调用opencv-cv2的方法就可以实现方法。如resize(img,(700,700),cv2.INTER_NEAREST)为最近邻插值法，resize(img,(700,700),cv2.INTER_LINEAR)为双线性插值法。在实际过程中，需要高分辨率则用双线性插值法，但是这样需要耗费较多CPU，选用最近邻插值法运行很快但是图像有些许失真。所以具体选用哪种方法，根据实际情况衡量好精度和算力。

• 注：由于图片本身分辨率不高，所以看上去可能区别不大，但是对于电脑而言，在进行识别或者分割等操作时，差别还是很大的。