训练营第三十五天动态规划(part1)
需要用到之前的数据
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
力扣题目链接
题目
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
解答
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
class Solution {
public int fib(int n) {
if (n == 0 || n == 1)
return n;
int[] dp = new int[n + 1];//记录每次的斐波那契数
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
70. 爬楼梯
力扣题目链接
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
提示:
1 <= n <= 45
解答
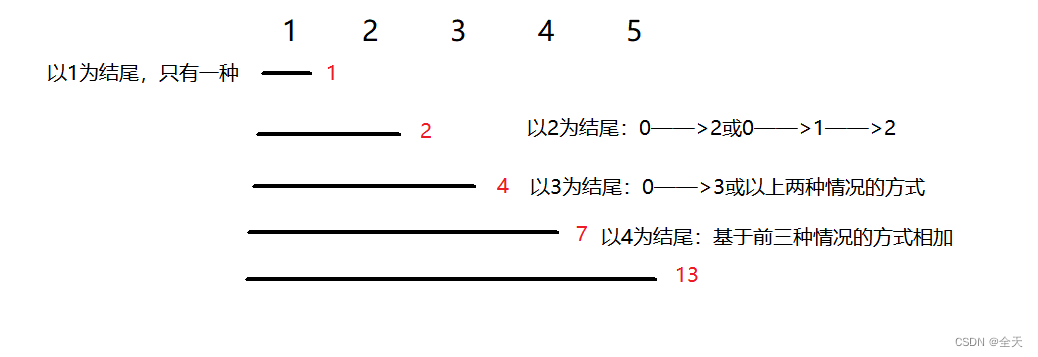
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯和到第一层楼梯状态推导出来
五部曲
- 确定dp数组以及下标的含义 dp[i]: 爬到第i层楼梯,有dp[i]种方法
- 确定递推公式 dp[i] = dp[i - 1] + dp[i - 2]
- dp数组如何初始化 不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推
- 确定遍历顺序 从前向后
- 举例推导dp数组(验证结果)
class Solution {
public int climbStairs(int n) {
int[] dp = new int[n + 1];//不要0
if (n <= 2)
return n;
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}
优化空间复杂度
class Solution {
public int climbStairs(int n) {
if(n <= 2) return n;
int a = 1, b = 2, sum = 0;
for(int i = 3; i <= n; i++){
sum = a + b; // f(i - 1) + f(i - 2)
a = b; // 记录f(i - 1),即下一轮的f(i - 2)
b = sum; // 记录f(i),即下一轮的f(i - 1)
}
return b;
}
}
746. 使用最小花费爬楼梯
力扣题目链接
题目
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
解答
- 确定dp数组以及下标的含义 dp[i]:到达第i台阶所花费的最少体力为dp[i]
- 确定递推公式 dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
- dp数组如何初始化 dp[0] = 0,dp[1] = 0;
- 确定遍历顺序 从前向后
- 举例推导dp数组(验证结果)
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length + 1];
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i <= cost.length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.length];
}
}