文章目录
- 0. 前言
- 1. 算法分析
- 2.级数
- 2.1基本形式
- 2.2 收敛级数
- 3.循环 vs 级数
- 4.示例
0. 前言
通过以基本计算模型作为参照,并且以大O记号的形式在上面添加适当刻度,已经建立一套对DSA进行分析的完整工具和体系。不清楚的可以看看复杂度度量 、复杂度分析和递归分析
接下来学习下如何运用工具对DSA进行性能分析,包括其中主要思路和方法。与这套体系建立的思路类似,我们在具体运用这套体系的时候,依然要坚持去粗存精,最终的学习目标是能够达到自如驾驭和运用这套工具来完成去粗存精式的估算。
1. 算法分析

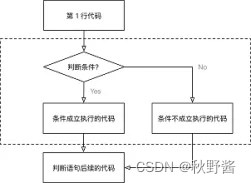
算法分析任务主要包括两方面内容,一是算法自身的正确性证明,下面会给出一种主要的办法,就是通过挖掘算法具有的不变性和单调性来证明。其次,是复杂度的分析和鉴定。
复杂度分析方法大概可以分为迭代、递归和猜测+验证。
2.级数
2.1基本形式

2.2 收敛级数

级数中的各项会逐次递减,而且这种递减的速度足够快,以至于尽管每一项都是保持正数,但是总和不会超过某一个上界,虽然数值不同,但是从渐进意义上讲都可以视作常数。因此从大0记号角度看,都可以记作是O(1)。
每一项都是分数的级数有必要讨论吗?
假设某段代码的迭代循环可以等效地描述为硬币地投掷过程,正面概率为
λ
\lambda
λ,0 <
λ
\lambda
λ < 1,反过来投掷反面地概率为1-
λ
\lambda
λ。程序运行可能等效于不断投掷一枚硬币,直到第一次出现反面,算法复杂度取决于整个投掷过程中总共投掷了多少次硬币。解就是1/(1-
λ
\lambda
λ )。
λ
\lambda
λ 是常数,所以复杂度是0(1)。
另一类级数虽然未必收敛,但是长度有限,以至于界会经常用到,典型地有两个调和级数(logn)和对数级数(nlogn)。
3.循环 vs 级数
如何分析代码段中所涉及地循环操作复杂度?

强记就OK

外部控制变量i从0变化到n,意味着内循环必然也是n趟,每一趟长度不是简单地0到i,等效于每一趟内循环地累计长度缩减到固定的2013分之一。
外循环控制变量每次都是加倍,换而言之,内循环长度j将以2为倍数,呈现出一个几何级数地形式,最大值由n决定。

4.示例



通过挖掘并且综合算法所具有地不变性和单调性,进而证明正确性地方法是算法分析地基本且重要的技巧。



![Qt [获取Dump] 使用WindowsAPI实现生成MiniDump文件](https://img-blog.csdnimg.cn/direct/e81e510b426c42aca819bcb545f1087b.png)