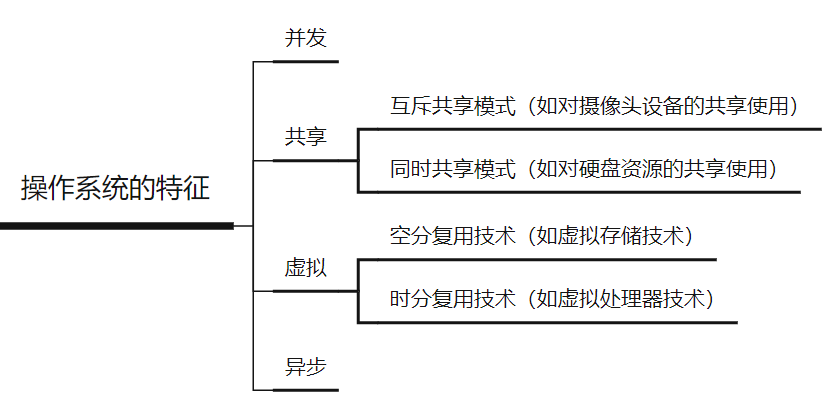
填充和步幅

• 卷积核带来的问题—输入形状不断减小
• 更大的卷积核可以更快的减小输出大小
  • 形状从$n_h\ast n_w$减少到
    $$(n_h-k_h+1)\ast (n_w-k_w+1)$$
• 解决方案
  • 填充—在输入周围添加额外的行/列—一般用0填充
  • 理论依据
    • 填充$p_h$行$p_w$列，输出形状为
      $$(n_h-k_h+p_h+1)\ast (n_w-k_w+p_w+1)$$
    • 为了保证输出结构的不变化我们一般取
      $$p_h=k_h-1,p_w=k_w-1$$
  • 步幅—每次卷积核移动的步数
  • 输入大小比较大的时候，输出可以成倍减少
  • 理论依据
    • 给定高度$s_h$和宽度$s_w$的步幅，输出形状是
      $$\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \ast \lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor$$
    • 如果$p_h=k_h-1$, $p_w=k_w-1$
      $$\lfloor (n_h+s_h-1)/s_h\rfloor \ast \lfloor (n_w+s_w-1)/s_w\rfloor$$
    • 如果输入高度和宽度可以被步幅整除
      $$(n_h/s_h)\ast (n_w/s_w)$$
• 总结
  • 填充和步幅是卷积层的超参数
  • 填充在输入周围添加额外的行/列，来控制输出形状的减少量
  • 步幅是每次滑动核窗口时到行/列的步长，可以成倍的减少输出形状
• 代码实现

import torch
from torch import nn
def com_conv2d(conv2d, X):
  X = X.reshape((1, 1)+X.shape)
  Y = conv2d(X)
  return Y.reshape(Y.shape[2:])
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
# padding就是填充
conv2d = nn.Conv2d(1, 1, kernel_size(5, 3), padding=(2, 1))
# 上下填充2*2行左右填充1*2
nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
# 上下填充0*2行左右填充1*2行，行间步长为3，列间为4

多输入输出通道

• 多个输入通道

  • 彩色图像可能有RGB三个通道
  • 转换为灰度会丢失信息
  • 每个通道都有一个对应的卷积层，结果是所有通道卷积结果的和—卷积有多通道融合性能
    

• 多个输出通道

  • 无论有多少输入通道，到目前为止我们只用到单输出通道
  • 我们可以有多个三维卷积核，每个核生成一个输出通道
    

• 多个输入和输出通道

  • 每个输出通道可以识别特定模式
  • 输入通道核识别并组合输入的模式

• 1*1卷积层

  • 它不识别空间模式，只是通道融合功能
  • 相当于输入形状为$n_h{n}_w\ast c_i$,权重为$c_o\ast c_i$的全连接层

• 总结

  • 输出通道是卷积层的超参数
  • 每个输入通道有独立的二维卷积核，所有通道结果相加得到一个输出通道结果
  • 每个输出通道有独立的三维卷积核
  • 我们可以理解每一层卷积层都是将上一层识别出来的小模式放入本层，进行更大面积的模式识别，就像识别一个猫，可以首先识别其眼睛而后到头部，最后得到全部特征

• 代码实现多输入输出

  • 从零实现

  import torch
  from d2l import torch as d2l
  # 定义多通道输入
  def corr2d_multi_in(X, K):
      return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
      # 将不同通道的进行卷积操作，而后进行融合
  X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
                    [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
  K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
  # 定义多通道输出
  corr2d_multi_in(X, K)
  def corr2d_multi_in_out(X, K):
      return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
  # k是将K中的四维取出三个维度与输入进行卷积而后形成一个卷积后的列表 在dim=0维度上堆积起来
  # k in K就是遍历每一层卷积核
  K = torch.stack((K, K + 1, K + 2), 0)
  K.shape
  corr2d_multi_in_out(X, K)
  # 利用全连接实现1*1的卷积
  def corr2d_multi_in_out_1x1(X, K):
      c_i, h, w = X.shape
      c_o = K.shape[0]
      X = X.reshape((c_i, h * w))
      K = K.reshape((c_o, c_i))
      Y = torch.matmul(K, X)
      return Y.reshape((c_o, h, w))
  
  X = torch.normal(0, 1, (3, 3, 3))
  K = torch.normal(0, 1, (2, 3, 1, 1))
  
  Y1 = corr2d_multi_in_out_1x1(X, K)
  Y2 = corr2d_multi_in_out(X, K)
  assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
  

  • 调用pytorch实现

  net = nn.Conv2d(1, 2, kernel_size=3, padding=1, stride=2)
  # 输出通道为2输入通道为1
  

池化层

• 卷积层的不足
  • 具有良好的特征提取功能但对位置太敏感
• 池化层—需要一定程度的平移不变性—弱化位置的敏感性
• 池化层的两种常见形式
  • 最大池化
    • 2*2的池化面积—$max(0,1,2,3)=3$
  • 均值池化
    • 2*2的池化面积—求解对应区间的均值
• 填充、步幅和多个通道
  • 池化层和卷积层类似，都具有填充、步幅和窗口大小这三类超参数
  • 缓解卷积层带来的位置高度敏感性
  • 没有可学习参数
  • 在每个输入通道应用池化层以获得相应的输出通道—不会和卷积一样进行同一维度多通道融合
  • 输出池化层的通道数=输入池化层的通道数
• 代码实现
  • 从零实现

  import torch
  from torch import nn
  from d2l import torch as d2l
  def pool2d(X, pool_size, model='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))# 生成输出大小
    for i in range(Y.shape[0]):
      for j in range(Y.shape[1]):
        if model == 'max':
          Y[i, j] = X[i:i+p_h, j:j+p_w].max()
        elif model == 'avg':
          Y[i, j] = X[i:i+p_h, j:j+p_w].mean()
    return Y
  

  • 调用pytorch实现

  pool2d = nn.MaxPool2d(3) # 默认是一个3*3的窗口步幅也是3
  pool2d = nn.MaxPool2d((2, 3), padding=(1,1), stride=(2, 3))
  # 根据通道的输入会时生成多个通道的池化层