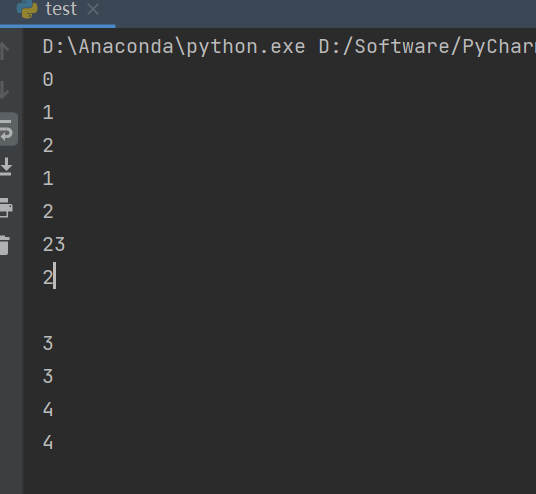
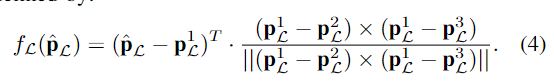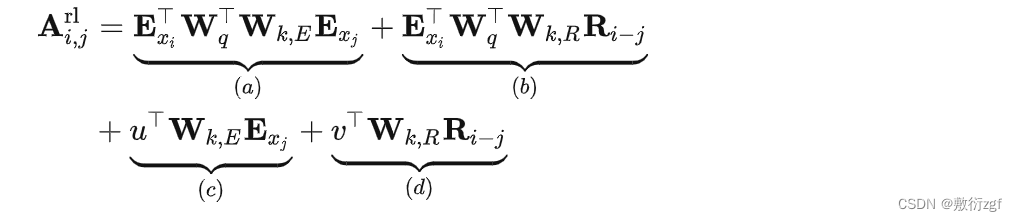高精度存在的意义

大家一定都知道int和long long是有极限的（如下表），如果超了就无法计算正确结果了，那该用什么方法来计算呢？这就是我们今天要说的算法———高精度算法。（本文只讲加法）

类型	存储字节	表示范围
int	4	1e9+             -2147483648～2147483647
long long	8	1e18+           -9223372036854775808~9223372036854775808

高精度实现原理

正常我们列的加法算式是这样的（如下图），这也是我们的期待方式，但是计算机能识别吗？

         

答案是——能。但是这样的代码不仅时间复杂度高，而且代码还十分复杂。

如果我们正常遍历，从0开始的话，就会变成这样子（如下图）。

           

这显然与我们的正确答案224相距甚远，肯定不是这样的。

那如果我们倒叙存储（当然也要倒着算）呢？就会变成这样（如下图）。

          

 我们把结果422倒过来就是224了，和正确答案224一模一样。成功了。

算法实现

核心思路

就像是列的竖式算式一样。按位相加，不要忘记处理进位的问题。如果这一位大于9，那么就把他的上一位加1，本位mod10。

代码如下：

	//核心代码 
	for(int i = 0; i < max(strlen(a1), strlen(b1)); i++)
	{ 
		result[i] += (a[i] + b[i]); 	//按位相加 
		result[i + 1] = result[i] / 10; //进位 
		result[i] %= 10; 				//本位mod10 
	}

算法过程

1.把输入的2个字符串加数倒序存储到2个int类型的数组里。

2.按照核心思路处理

3.倒序输出答案。这里有一个小细节，如果最高位大于9，则需要多输出一个result[i]

完整代码

完整代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 2010; 
char a1[N], b1[N];//分表表示字符串类型的两个加数 
int a[N], b[N], result[N];//a[],b[]表示int类型的两个加数，方便运算， 
int main()
{
	cin >> a1 >> b1;
	//倒序存储 
	for(int i = 0; i < strlen(a1); i++)
	{
		a[strlen(a1) - 1 - i] = a1[i] - '0';	
	}
	for(int i = 0; i < strlen(b1); i++)
	{
		b[strlen(b1) - 1 - i] = b1[i] - '0';	
	}
	//核心代码 
	for(int i = 0; i < max(strlen(a1), strlen(b1)); i++)
	{ 
		result[i] += (a[i] + b[i]); 	//按位相加 
		result[i + 1] = result[i] / 10; //进位 
		result[i] %= 10; 				//本位mod10 
	}
	//看看加完之后的结果用不用进位
	int add = 0; 
	if(result[max(strlen(a1), strlen(b1))] != 0)
	{
		add = 1; 
	}
	//倒序输出 
	for(int i = max(strlen(a1), strlen(b1)) + add - 1; i >= 0; i--)
	{
		cout << result[i];
	}
	return 0;
}

 这样高精度加法就完美解决了！

请您点赞关注加收藏，您的点赞是我更新最大的动力。