1. 前言
今天的目的是为了深入了解下优先队列的机制。不过优先队列是基于
大小顶堆实现的,但是其本质就是一个二叉树,所以今天会讲一些铺垫知识,好了,废话不多说了,让我们开始吧
2. 前置知识
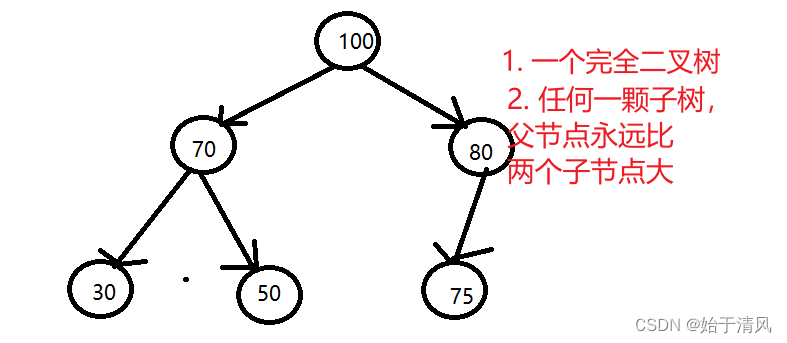
2.1 大顶堆
-
完全二叉树:
- 一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为 i(1≤i≤n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
- 一棵深度为 k 且有个结点的二叉树称为满二叉树
- 叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部
- 如果完全二叉树缺少节点,那一定在右侧

-
大顶堆:
- 必须是一个完全二叉树(满足二叉树的所有的性质)
- 任何子树中必须满足父元素大于任何子元素的值
-
需要实现的方法:
peek(): T | boolean查询堆顶的数据,但是不修改数据poll(): T | boolean从堆顶弹出一个元素,调整结构(堆尾元素添加到堆顶,并且开始下调整)offer(value: T): boolean从堆底添加一个元素,调整结构(上调整)isEmpty(): boolean判断堆是否为空size(): number返回堆的长度
-
实现案例
- 求最值 场景使用最多(比如:获取前 5 个最小值)
2.2 小顶堆

-
完全二叉树:
- 一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为 i(1≤i≤n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
- 一棵深度为 k 且有个结点的二叉树称为满二叉树
- 叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部
- 如果完全二叉树缺少节点,那一定在右侧

-
小顶堆:
- 必须是一个完全二叉树(满足二叉树的所有的性质)
- 任何子树中必须满足父元素小于任何子元素的值
-
需要实现的方法:
peek(): T | boolean查询堆顶的数据,但是不修改数据poll(): T | boolean从堆顶弹出一个元素,调整结构(堆尾元素添加到堆顶,并且开始下调整)offer(value: T): boolean从堆底添加一个元素,调整结构(上调整)isEmpty(): boolean判断堆是否为空size(): number返回堆的长度
-
实现案例
- 求最值 场景使用最多(比如:获取前 5 个最大值)
3. 优先队列
3.1 构造函数
既然是优先队列,就需要通过比较大小来决定谁先输出。被添加的元素要实现了
Comparator接口,可以进行比较.

3.1.1 基本构造属性
// 数组的默认长度。 虽然是一个完全二叉树,但是底层是基于数组来实现的
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// 表示数组的最大值。 减8的目的是为了兼容不同的JDK版本
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
// 存储元素的地方
private transient Object[] queue;
// 用来表示队里的长度
private transient int size;
// 此处是比较器
private transient Comparator<? super E> comparator;
// 此处表示一个锁
private final ReentrantLock lock;
// 表示消费者挂起condition
private final Condition notEmpty;
// 目的是为了避免并发扩容
private transient volatile int allocationSpinLock;
3.1.2 构造函数实现
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
// 如果长度小于1的话 直接报错
if (initialCapacity < 1)
throw new IllegalArgumentException();
// 实例化锁
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
// 表示比较器
this.comparator = comparator;
// 表示存储对象的数组
this.queue = new Object[initialCapacity];
}
3.2 生产者方法
3.2.1 add
public boolean add(E e) {
// add方法 本质上就是调用offer方法
return offer(e);
}
3.2.2 offer
public boolean offer(E e) {
// 添加的元素不能为null 如果为null的话 直接报错
if (e == null)
throw new NullPointerException();
// 局部变量 获取锁实例
final ReentrantLock lock = this.lock;
// 上锁
lock.lock();
int n, cap;
Object[] array;
// queue 表示的数组本身
// size 优先级中队列元素
// 如果优先队列中元素 >= 数组的长度的话 直接选择扩容
while ((n = size) >= (cap = (array = queue).length))
// 扩容方法
tryGrow(array, cap);
try {
// 执行到此时 表示要么扩容成功 要么就不满足while条件
Comparator<? super E> cmp = comparator;
// 如果cmp 比较器 为null的话
if (cmp == null)
// n 表示size长度
// e 表示添加的元素
// array 优先级队列本身
siftUpComparable(n, e, array);
else
siftUpUsingComparator(n, e, array, cmp);
// 表示size 累加
size = n + 1;
// 通过消费者 开始消费。 因为有可能之前队列是空的 消费者消费时导致线程挂起
notEmpty.signal();
} finally {
lock.unlock();
}
return true;
}
3.2.3 小顶推实现
- 如果想实现小顶堆,应该牢记小顶堆的原理。
任意一个元素,都比其子元素要小- 如果
root节点应该是最小的值- 为了维护这种关系,我们应该向上查找,直到找到比当前值小的值为止
private static <T> void siftUpComparable(int k, T x, Object[] array) {
// 此时表示添加的元素 。元素实现了Comparable 比较器
Comparable<? super T> key = (Comparable<? super T>) x;
// 此while循环是一个小顶堆实现原理
while (k > 0) {
// 虽然小顶堆是完全二叉树,但是存放顺序可以放到数组中。 如果是子元素寻找父亲的话可以是`(k - 1) >>> 1`
int parent = (k - 1) >>> 1;
// 找到父亲的位置 获取对应的值
Object e = array[parent];
// 将当前元素 跟父类元素比较 应该是 当前的值 - 父亲的值 >= 0. 因为是小顶堆 所以应该向上找比当前值 更小的值
if (key.compareTo((T) e) >= 0)
break;
// 移动父亲的位置
array[k] = e;
// 当前parent 成为新的key
k = parent;
}
// 设置最小的值
array[k] = key;
}
3.2.4 扩容数组实现原理
- 这里简单简述下 整个数组扩容的思想:
- 如果原来的数组长度 < 64 的话,设置新的长度是 旧长度 * 2 + 2
- 如果原来的数组长度 >= 64的话,设置的新的长度是 旧长度 * 1.5
- 然后比较是否超过最大长度等等 做一系列长度
// 此方法是一个数组扩容方法
// oldCap 原数组队列的长度
// array 是一个原数组
private void tryGrow(Object[] array, int oldCap) {
// 解锁
lock.unlock();
// 新的数组
Object[] newArray = null;
// allocationSpinLock 为 0的时候 表示目前没有线程 处于一个扩容的状态
if (allocationSpinLock == 0 &&
// 通过CAS 进行allocationSpinLock值设置。 保证了线程安全。
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) {
// 如果数组的长度 < 64 的话 实际长度就是oldCap * 2 + 2 反之 oldCap * 1.5
try {
int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // grow faster if small
(oldCap >> 1));
// 如果设置的新的长度 比 最大值还大
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
// 扩容最小长度 = 旧数组长度 + 1
int minCap = oldCap + 1;
// 如果为负值 或是 最小都比MAX_ARRAY_SIZE 大的话 直接就是溢出异常
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
// 将新数组长度 设置为 MAX_ARRAY_SIZE
newCap = MAX_ARRAY_SIZE;
}
// 设置新的长度 > 原来的长度 && 数组没有变化
if (newCap > oldCap && queue == array)
newArray = new Object[newCap];
} finally {
allocationSpinLock = 0;
}
}
if (newArray == null) // back off if another thread is allocating
Thread.yield();
lock.lock();
// 新的数组 以及被实例化了 && 原数组本身没有变化
if (newArray != null && queue == array) {
// 进行值copy
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
3.2.5 有参offer
public boolean offer(E e, long timeout, TimeUnit unit) {
// 可以理解为优先级队列是无界的 因为一直在扩容。 所以不会存在队满的情况,所以不需要等待
return offer(e); // never need to block
}
3.2.6 put
public void put(E e) {
// 此处表示直接添加 绝不会blocking住
offer(e); // never need to block
}
3.3 消费者方法
3.3.1 remove
public E remove() {
// 表示删除一个元素
E x = poll();
// 如果删除的元素不为null的话 直接返回值
if (x != null)
return x;
else
// 如果为null的话 直接抛出异常
throw new NoSuchElementException();
}
3.3.2 poll
public E poll() {
// 获取锁实例
final ReentrantLock lock = this.lock;
// 加锁
lock.lock();
try {
// 返回提出的值
return dequeue();
} finally {
// 解锁
lock.unlock();
}
}
// 此方法是获取堆顶的元素
private E dequeue() {
// 表示-1 后的长度
int n = size - 1;
// 如果是<0的话 表示是空队列
if (n < 0)
return null;
else {
// 如果执行到此处表示不是空队列
Object[] array = queue;
// 获取堆顶元素
E result = (E) array[0];
// 获取最后一个元素
E x = (E) array[n];
// 最后一个元素重置为null
array[n] = null;
// 比较器
Comparator<? super E> cmp = comparator;
if (cmp == null)
// 元素下沉
siftDownComparable(0, x, array, n);
else
siftDownUsingComparator(0, x, array, n, cmp);
size = n;
return result;
}
}
3.3.3 维护堆,下沉方法
// 为了维护堆中元素 实现下沉的方法
// k 此时的值 为 0
// x 原来堆中最后一个元素 其实就是最大元素
// array 表示队列中的原数组
// n 队列中长度 - 1
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
// 如果n<= 0 表示 此时队列中没有数据 所以没有必要下沉
if (n > 0) {
// 此时元素 实现了Comparable 比较器
Comparable<? super T> key = (Comparable<? super T>)x;
// 一半
int half = n >>> 1; // loop while a non-leaf
while (k < half) {
// 左子元素
int child = (k << 1) + 1; // assume left child is least
// 左子元素值
Object c = array[child];
// 右子元素下标
int right = child + 1;
// 左右子树进行比较 如果左子树 > 右子树
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
c = array[child = right];
// 如果父元素 已经比子树小了 就到头了
if (key.compareTo((T) c) <= 0)
break;
// 重新设置元素 以及下标
array[k] = c;
k = child;
}
array[k] = key;
}
}
3.3.4 有参poll
// 表示延迟时间 timeout
public E poll(long timeout, TimeUnit unit) throws InterruptedException {
// 格式化时间 统一转换为纳秒
long nanos = unit.toNanos(timeout);
// 获取锁实例
final ReentrantLock lock = this.lock;
// 上锁
lock.lockInterruptibly();
E result;
try {
// 队列中没有数据 && 还有等待时间
while ( (result = dequeue()) == null && nanos > 0)
// 暂时挂起线程
nanos = notEmpty.awaitNanos(nanos);
} finally {
lock.unlock();
}
return result;
}
3.3.5 take
public E take() throws InterruptedException {
// 获取锁实例
final ReentrantLock lock = this.lock;
// 上锁 可被打断锁
lock.lockInterruptibly();
E result;
try {
// 如果队列中没有数据 然后挂起线程 反之就是一直等待
while ( (result = dequeue()) == null)
notEmpty.await();
} finally {
lock.unlock();
}
return result;
}
4. 结束
代码就分析到这里了。其实核心内容就是:
扩容机制和 通过小顶堆如何维护队列的数据结构。 上述的代码中每一行代码都标注了注释,如果大家还有什么疑问的话,欢迎及时留言区评论。