参考文献：

• [1]乔珊. 主动配电网多源协同运行优化研究[D]. 山东大学, 2021. 
• [2]高红均,刘俊勇,沈晓东,等. 主动配电网最优潮流研究及其应用实例 [J]. 中国电机工程学报, 2017, 37 (06): 1634-1645. DOI:10.13334/j.0258-8013.pcsee.152839.

1.引言

        主动配电网技术的发展已成为大势所趋，如何协调主动配电网中的各元件进行协同和优化，使可再生能源充分被消纳，是亟待解决的问题。本文针对主动配电网中的主要组成部分，包括分布式电源、储能系统、电动汽车、无功补偿装置等，分析其出力特性及可调潜力，对其进行数学建模，从保障配电网安全稳定运行角度出发，尽量降低运行成本，构建多时间尺度优化调度模型。在优化调度过程中，在满足经济效益最优的同时实现对分布式电源出力的最大化消纳，尽量缩减潮流分布的峰谷差，实现“源”、“荷”、“储”的多方面协同优化运行。

2.主动配电网模型

        在主动配电网框架下,主动管理包括: 1)OLTC调节;2）无功装置调节，包括离散无功补偿和连续无功调节;3）有功调节，包括储能调节以及电动汽车调节;4）分布式电源自身调节。同样，需求响应作为主动配电网的重要参与元素也应充分利用。此外，为适应模型的通用性，文中也增加了综合负荷模型。由于最优潮流的目标函数基本为线性或二次形式，二次形式也能通过分段线性等方式进行转化，且效果均较满意，因此本文主要侧重于对各主动管理设备相关的约束条件进行线性建模处理。此外根据文献[2]知，网络灵活性在主动配电网规划运行中举足轻重,其主要思想为网络重构(开关调节)。本文对网络重构相关约束限制也进行了探讨，如辐射性约束等。

2.1 OLTC建模

2.2 无功调节装置建模

2.3 储能装置建模

2.4 分布式电源建模

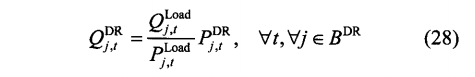
        上式为最简单的负荷响应与电网交互方式，认为无功等比例变化于有功功率，实际上，无功需求也是一个较为复杂的问题，本文不予讨论。

3.运行结果展示

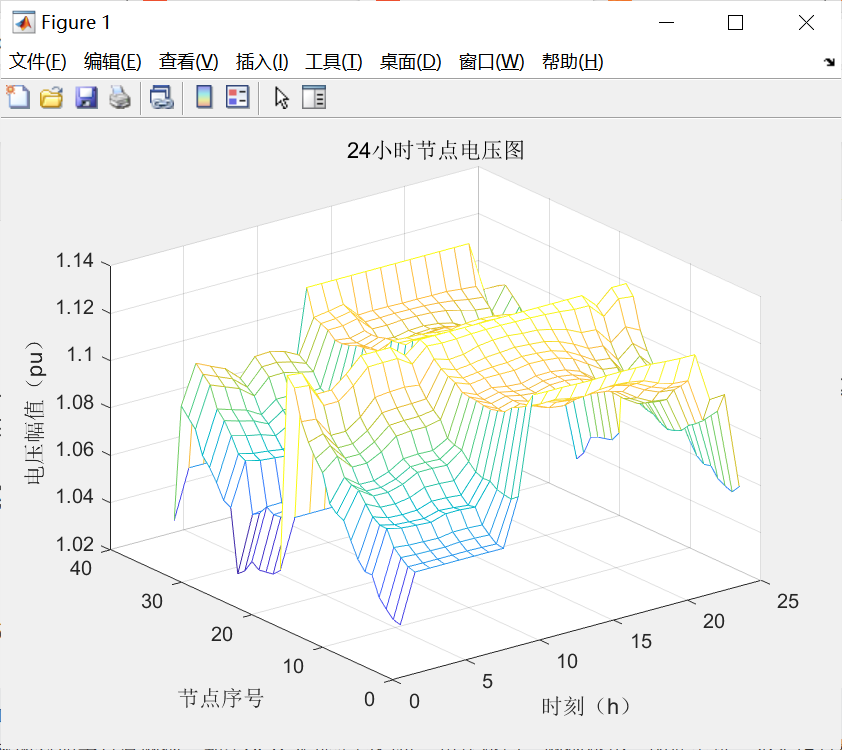
4.matlab代码

%多时段+SVC+CB+OLTC+DG SOCP_OPF   Sbase=1MVA,   Ubase=12.66KV
%目标函数如果只有网损，那么OLTC永远是高挡位，电压越高，网损越小，因此需进一步考虑目标函数如主网购电，或者电压平衡          

%%
%有载调压变压器的位置在那个节点

%%
clear 
clc 
tic 
warning off
%% 1.设参
mpc = IEEE33BW;
wind = mpc.wind;    
pload = mpc.pload;    
pload_prim = mpc.pload_prim/1000;  %化为标幺值
qload_prim = mpc.qload_prim/1000;
a = 3.715;   %单时段所有节点有功容量,MW
b = 2.3;     %单时段所有节点无功容量,MW
pload = pload/a;%得到各个时段与单时段容量的比例系数
qload = pload/b;%假设有功负荷曲线与无功负荷变化曲线相同
pload = pload_prim*pload;   %得到33*24的负荷值，每一个时间段每个节点的负荷
qload = qload_prim*qload;      

branch = mpc.branch;       
branch(:,3) = branch(:,3)*1/(12.66^2);%求阻抗标幺值      
R = real(branch(:,3));            
X = imag(branch(:,3));             
T = 24;%时段数为24小时             
nb = 33;%节点数            
nl = 32;%支路数           
nsvc = 3;%SVC数      静止无功补偿器 Static Var compensator
ncb = 2;%CB数        分组投切电容器组 (capacitorbanks，CB)
noltc = 1;%OLTC数    有载调压变压器 ( on—load tap changer，OLTC ）  transformer   
nwt = 2;%2个风机     
ness = 2;%ESS数      
upstream = zeros(nb,nl);
dnstream = zeros(nb,nl);
for i = 1:nl
    upstream(i,i)=1;
end
for i = [1:16,18:20,22:23,25:31]
    dnstream(i,i+1)=1;
end
dnstream(1,18) = 1;
dnstream(2,22) = 1;
dnstream(5,25) = 1;
dnstream(33,1) = 1;
Vmax = [1.06*1.06*ones(nb-1,T)
        1.06*1.06*ones(1,T)];
Vmin = [0.94*0.94*ones(nb-1,T)
        0.94*0.94*ones(1,T)];%加入变压器后，根节点前移，因此不是恒定值1.06
Pgmax = [zeros(nb-1,T)
         5*ones(1,T)];
Pgmin = [zeros(nb-1,T)
         0*ones(1,T)];
Qgmax = [zeros(nb-1,T)
         3*ones(1,T)];
Qgmin = [zeros(nb-1,T)
         -1*ones(1,T)];
QCB_step = 100/1000;       %单组CB无功,100Kvar 转标幺值     
%% 2.设变量
V = sdpvar(nb,T);%电压的平方
I = sdpvar(nl,T);%支路电流的平方
P = sdpvar(nl,T);%线路有功（是不是平方我就不清楚了，应该不是）
Q = sdpvar(nl,T);%线路无功
Pg = sdpvar(nb,T);%发电机有功
Qg = sdpvar(nb,T);%发电机无功
theta_CB = binvar(ncb,T,5); %CB档位选择，最大档为5
theta_IN = binvar(ncb,T);%CB档位增大标识位
theta_DE = binvar(ncb,T);%CB档位减小标识位   

q_SVC = sdpvar(nsvc,T);%SVC无功    
p_wt = sdpvar(nwt,T);%风机有功     


p_dch = sdpvar(ness,T);   %ESS放电功率
p_ch = sdpvar(ness,T);   %ESS充电功率
u_dch = binvar(ness,T);%ESS放电状态
u_ch = binvar(ness,T);%ESS充电状态
E_ess = sdpvar(ness,25);%ESS的电量，这个25的原因要搞懂才能理解储能一天开始结束时刻（首末）功率相等的意思   

r1 = sdpvar(noltc,T);     
theta_OLTC = binvar(noltc,T,12);%OLTC档位选择，最大档为12
theta1_IN = binvar(noltc,T);%OLTC档位增大标识位
theta1_DE = binvar(noltc,T);%OLTC档位减小标识位
%% 3.设约束
C = [];        

.....省略......

%% 4.设目标函数
objective = sum(Pg(33,:))  +  0.3*sum(sum(I.*(R*ones(1,T))));   %子配电网向主网购电量 + 0.3*子配电网有功损耗
toc%建模时间
%% 5.设求解器
ops = sdpsettings('verbose', 1, 'solver', 'cplex');
ops.cplex= cplexoptimset('cplex');%这两句修改收敛间隙，使MIP问题跑的更快，酌情使用
ops.cplex.mip.tolerances.absmipgap = 0.01;

sol = optimize(C,objective,ops);

objective = value(objective)

toc%求解时间
% clear branch C dnstream upstream i kk mpc nb nl ncb ness noltc npv nwt nsvc...
%       QCB_step ops Pgmax Pgmin pload qload t T theta_DE theta_IN ...
%       Vmax Vmin R X P_ch P_dch P_pv P_wt Q_SVC Qgmax Qgmin Pin Qin...
%       Q_CB k r rjs theta1_DE theta1_IN 

%% 6.分析错误标志
if sol.problem == 0
    disp('succcessful solved');
else
    disp('error');
    yalmiperror(sol.problem)
end



% B = [1 2 3 ;
%     4 5 6 ;
%     7 8 9 ]
V = value(V);        
% for  i = 1 : 33   
%      VV(24*i - 23 : 24*i)   =  V(i,: );   
%      XX(24*i - 23 : 24*i) =   i;
%      YY(24*i - 23 : 24*i ) =  1:24;
% end  
% plot3(XX,YY,VV,'*');
figure(1)
[XX,YY] =meshgrid(1:24,1:33 );
mesh(XX,YY,V);
xlabel('时刻（h）');
ylabel('节点序号');
zlabel('电压幅值（pu）');
title('24小时节点电压图');

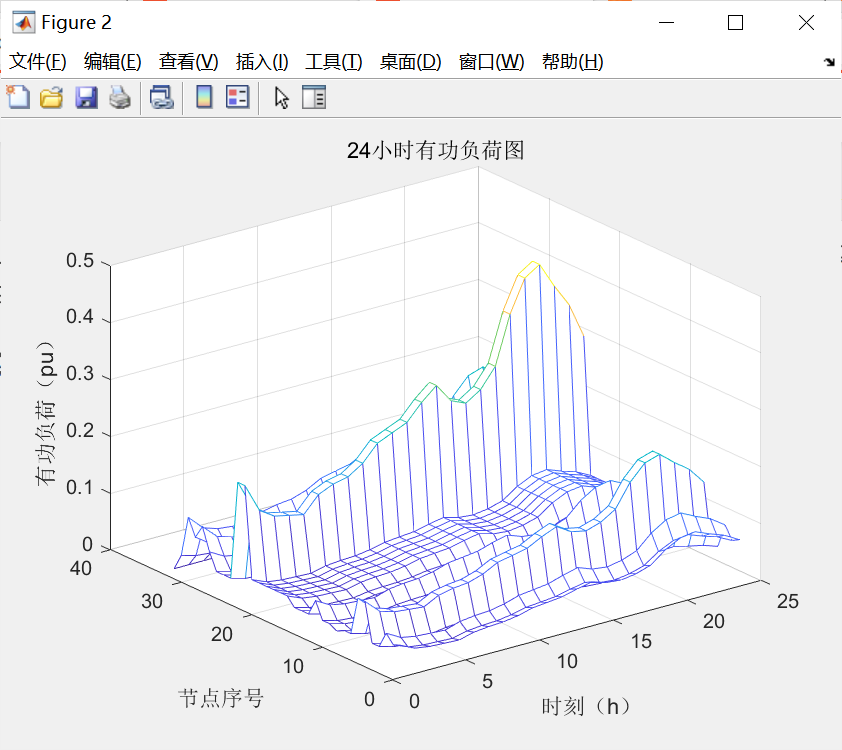
figure(2)
[XX,YY] =meshgrid(1:24,1:33 );
mesh(XX,YY,pload);     % pload需要进一步归算（利用pload_prim，a,b反推 ）
xlabel('时刻（h）');
ylabel('节点序号');
zlabel('有功负荷（pu）');
title('24小时有功负荷图');

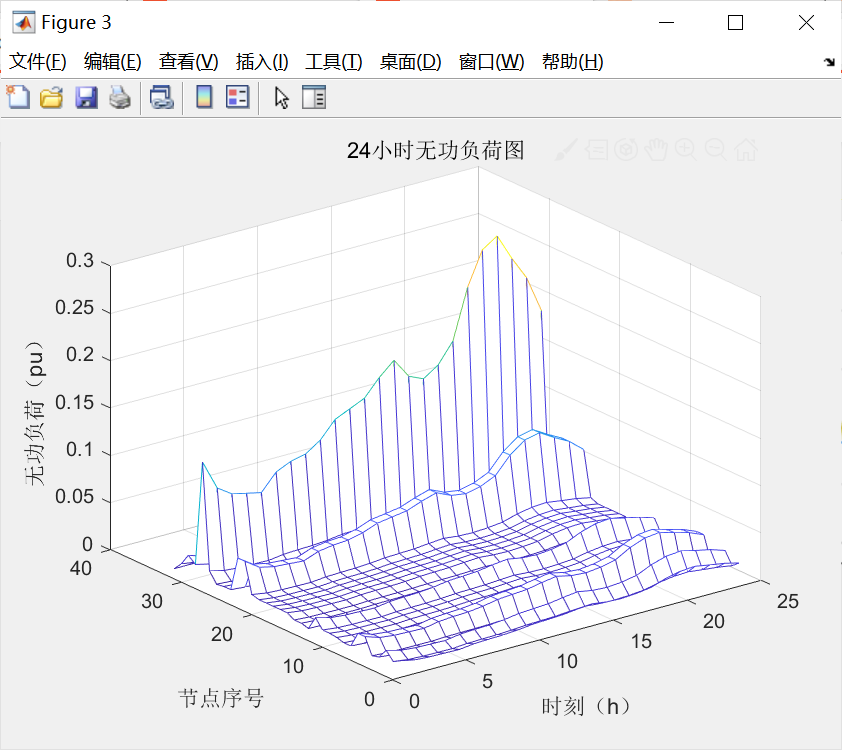
figure(3)
[XX,YY] =meshgrid(1:24,1:33 );
mesh(XX,YY,qload);
xlabel('时刻（h）');
ylabel('节点序号');
zlabel('无功负荷（pu）');
title('24小时无功负荷图');


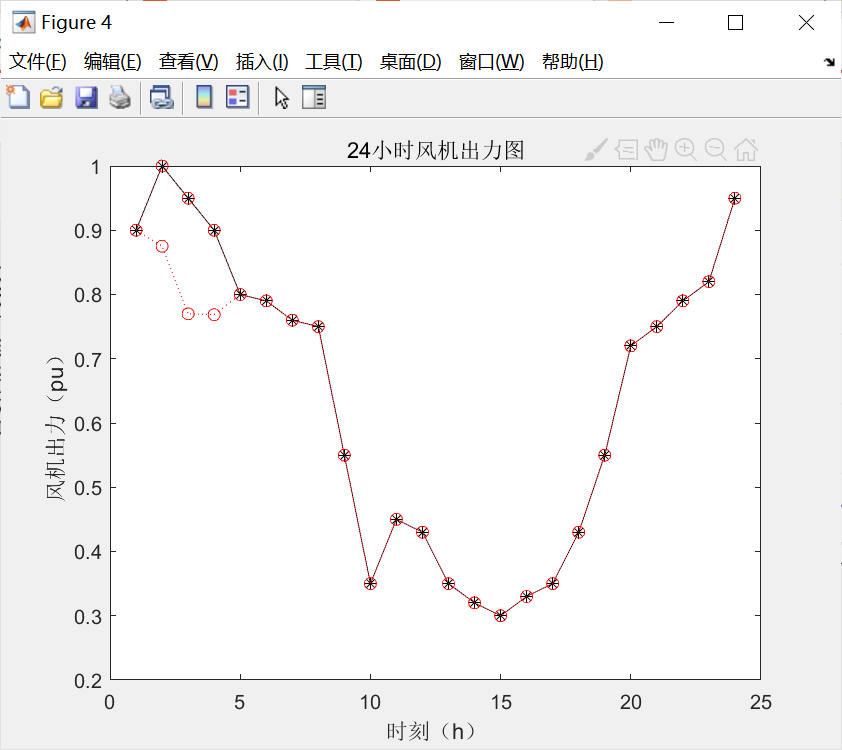
figure(4)
p_wt= value(p_wt);
plot(wind,'k-*');
hold on 
plot(p_wt',':ro');
xlabel('时刻（h）');
ylabel('风机出力（pu）');
title('24小时风机出力图');


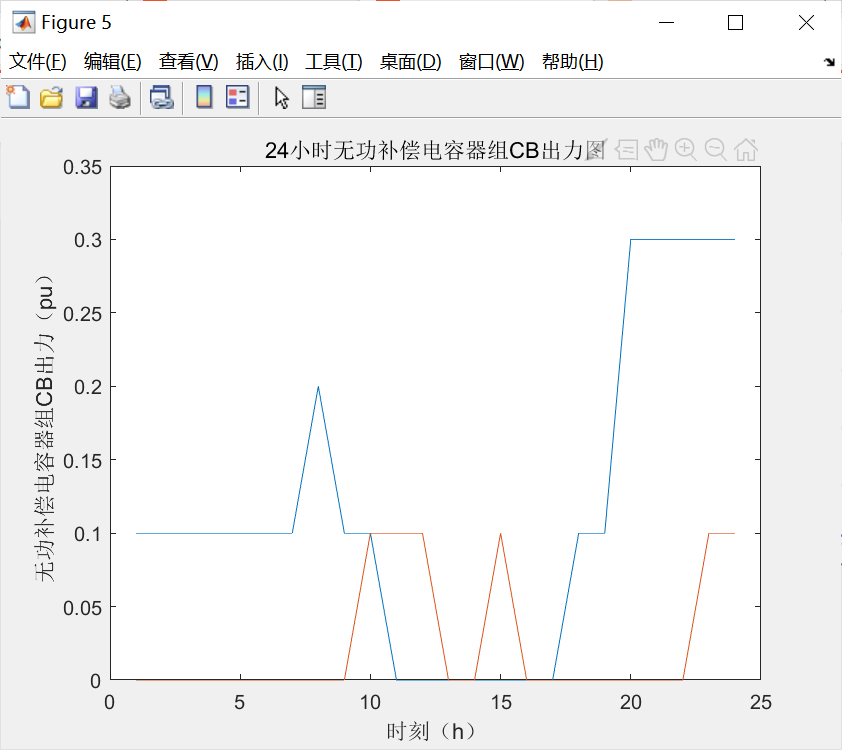
figure(5)
k= value(k);
Q_cb= value(Q_cb);
plot(Q_cb(1,:));
hold on 
plot(Q_cb(2,:));
xlabel('时刻（h）');
ylabel('无功补偿电容器组CB出力（pu）');
title('24小时无功补偿电容器组CB出力图');


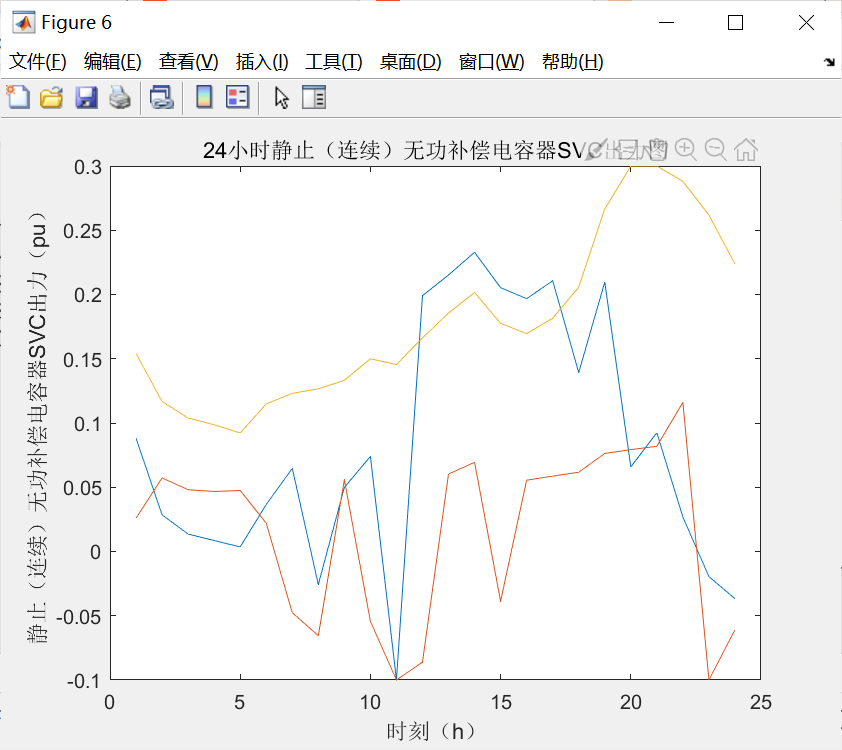
figure(6)
q_SVC = value(q_SVC);    
plot(q_SVC(1,:));
hold on 
plot(q_SVC(2,:));
hold on 
plot(q_SVC(3,:));
xlabel('时刻（h）');
ylabel('静止（连续）无功补偿电容器SVC出力（pu）');
title('24小时静止（连续）无功补偿电容器SVC出力图');


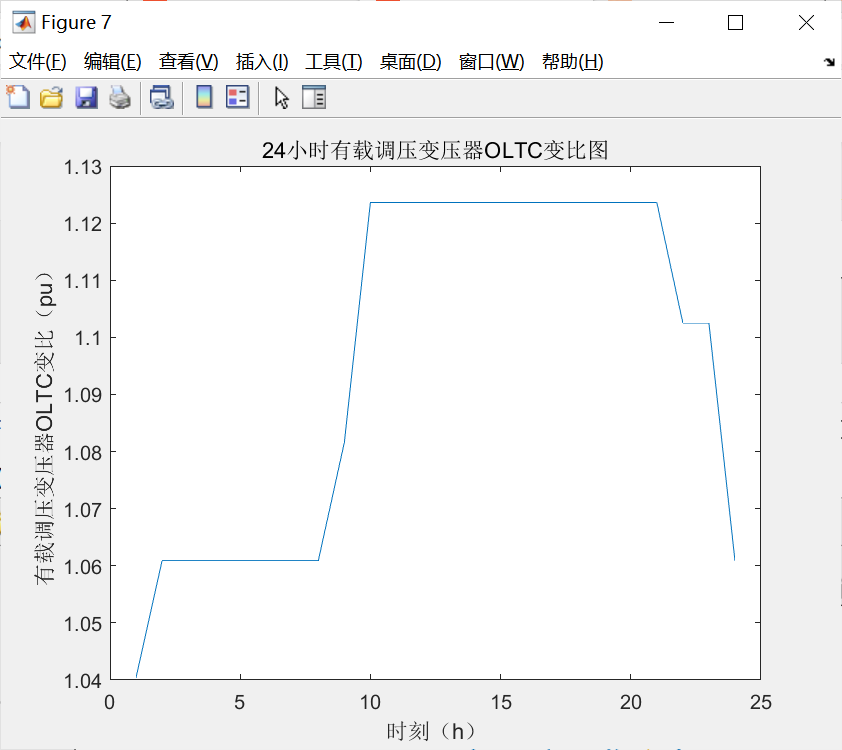
figure(7)
r1 = value(r1);    
plot(r1);
xlabel('时刻（h）');
ylabel('有载调压变压器OLTC变比（pu）');
title('24小时有载调压变压器OLTC变比图');


% p_dch = sdpvar(ness,T);   %ESS放电功率                
% p_ch = sdpvar(ness,T);   %ESS充电功率               
BA_dch = value(p_dch)*1.11;     
BA_ch = value(p_ch)*0.9;    
% BA_dch = value(p_dch);     
% BA_ch = value(p_ch);    
BA1 = BA_ch(1,:) - BA_dch(1,:);
BA2 = BA_ch(2,:) - BA_dch(2,:);
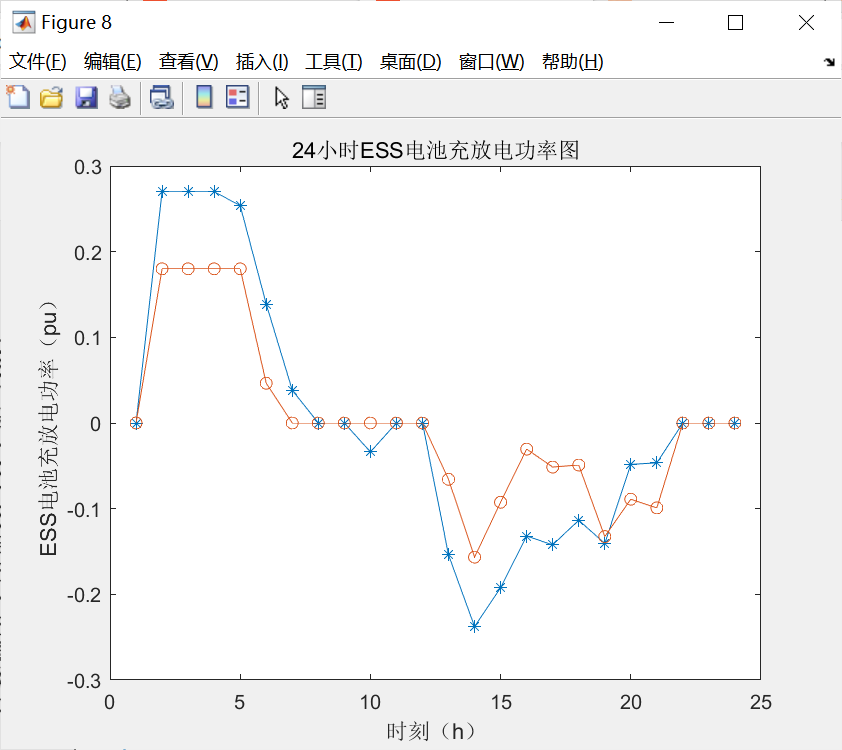
figure(8)  
plot(BA1,'-*');
hold on
plot(BA2,'-o');
xlabel('时刻（h）');
ylabel('ESS电池充放电功率（pu）');     
title('24小时ESS电池充放电功率图');       
BA1_P_Sum=sum(BA1);             
BA2_P_Sum=sum(BA2);  


E_ess=value(E_ess);
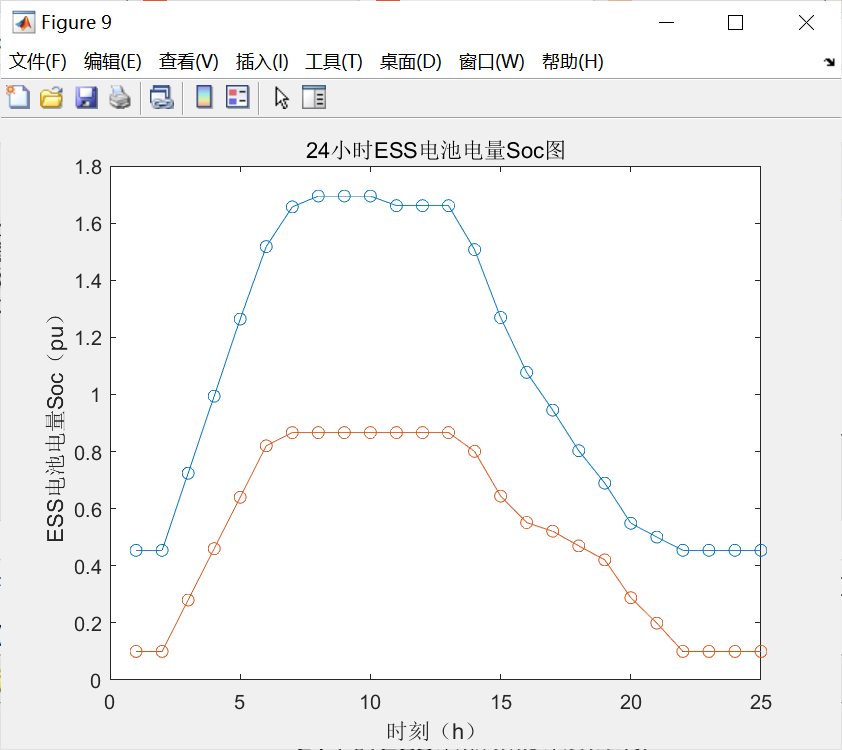
figure(9)
plot(E_ess','-o');
xlabel('时刻（h）');
ylabel('ESS电池电量Soc（pu）');     
title('24小时ESS电池电量Soc图');     

        以上仅为部分matlab代码，完整代码获取方式如下：

开源代码分享(23)-基于混合整数二阶锥规划(MISOCP)的主动配电网最优潮流matlab代码资源-CSDN文库