目录
- 1.数学介绍
- 2.使用多项式环进行加密
- 2.1 私钥和公钥的产生
- 2.2 加密
- 2.3 解密
- 3.同态计算
- 3.1 同态加法
- 3.2 同态乘法
1.数学介绍
同态加密方案基于一个难以计算的问题Ring Learning with Errorsred。这些方案中的数据在加密和未加密时都用多项式表示。
这里举一个简单的多项式:
4
x
2
+
2
x
+
1
4x^2+2x+1
4x2+2x+1 注意,其中的系数都是整数并且每个系数都会
m
o
d
t
mod \ t
mod t。 假设
t
=
24
t=24
t=24 ,如下图所示
21
+
6
=
3
m
o
d
24
21+6= 3 \ mod \ 24
21+6=3 mod 24。

或者我们可以将范围变为
[
−
11
,
12
]
[-11,12]
[−11,12],这样方便我们取负数。

我们定义了一个特殊的多项式,称为多项式模数,并且只考虑多项式在被这个多项式模数除后的余数。在FV方案中,这个多项式模数的具体形式是
x
d
+
1
x^d+1
xd+1,其中
d
=
2
n
d=2^n
d=2n,
n
n
n为某个整数。这里我们举例说明取
n
=
4
n=4
n=4,因此这个多项式是
x
16
+
1
x^{16}+1
x16+1
因为我们只考虑关于
x
16
+
1
x^{16}+1
x16+1后的余数,所以余数的中的多项式取值范围便为
[
x
0
,
x
15
]
[x^0,x^{15}]
[x0,x15],下面便是我们需要考虑的余数:
a
15
x
15
+
a
14
x
14
+
a
13
x
13
+
a
12
x
12
+
a
11
x
11
+
a
10
x
10
+
a
9
x
9
+
a
8
x
8
+
a
7
x
7
+
a
6
x
6
+
a
5
x
5
+
a
4
x
4
+
a
3
x
3
+
a
2
x
2
+
a
1
x
1
+
a
0
a_{15}x^{15}+a_{14}x^{14}+a_{13}x^{13}+a_{12}x^{12}+a_{11}x^{11}+a_{10}x^{10}+a_{9}x^{9}+a_{8}x^{8}+a_{7}x^{7}+a_{6}x^{6}+a_{5}x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x^{1}+a_{0}
a15x15+a14x14+a13x13+a12x12+a11x11+a10x10+a9x9+a8x8+a7x7+a6x6+a5x5+a4x4+a3x3+a2x2+a1x1+a0
其中系数
a
i
a_i
ai的取值范围为
{
0
,
t
−
1
}
\{0,t-1\}
{0,t−1},也就是说这里面的每个系数都会被
m
o
d
t
mod \ t
mod t,我们可以用系数环面来说明,如下所示:
 在该图中每个环代表一个
x
i
x^i
xi可以拥有24种系数的中一个。绿点代表系数为0。
在该图中每个环代表一个
x
i
x^i
xi可以拥有24种系数的中一个。绿点代表系数为0。
假设当我们让
2
x
14
a
n
d
x
4
2x^{14} and\ x^4
2x14and x4 相乘,同时
m
o
d
x
16
+
1
mod \ x^{16}+1
mod x16+1,将这个项(如下图中的红点所示)向前绕着环体旋转4个幂次,然后将值反射到0点的另一侧,变成了
22
x
2
22x^2
22x2。这个只是为了直观展示,方便后面的讲解,当然你也可以使用多项式除法进行计算,结果相同。

2.使用多项式环进行加密
2.1 私钥和公钥的产生
我们首先定义 d = 16 , t = 7 , q = 874 d=16,t=7,q=874 d=16,t=7,q=874,那么多项式的模便为 x 16 + 1 x^{16}+1 x16+1
对于密钥或者私钥 s s s,我们产生一个系数为 { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1}中的一个的随机多项式: s = x 15 − x 13 − x 12 − x 11 − x 9 + x 8 + x 6 − x 4 + x 2 + x − 1 s=x^{15}-x^{13}-x^{12}-x^{11}-x^9+x^8+x^6-x^4+x^2+x-1 s=x15−x13−x12−x11−x9+x8+x6−x4+x2+x−1
接下来我们产生一个公钥,使用密文空间中的随机多项式,其中系数 m o d q mod \ q mod q a = 42 x 15 − 256 x 14 − 393 x 13 − 229 x 12 + 447 x 11 − 369 x 10 − 212 x 9 + 107 x 8 + 52 x 7 + 70 x 6 − 138 x 5 + 322 x 4 + 186 x 3 − 282 x 2 − 60 x + 84 a=42x^{15}-256x^{14}-393x^{13}-229x^{12}+447x^{11}-369x^{10}-212x^9+107x^8+52x^7+70x^6-138x^5+322x^4+186x^3-282x^2-60x+84 a=42x15−256x14−393x13−229x12+447x11−369x10−212x9+107x8+52x7+70x6−138x5+322x4+186x3−282x2−60x+84
我们还定义了一个误差多项式,从离散高斯分布中提取出的“小”系数。这个多项式在这里只使用一次,然后被丢弃。 e = − 3 x 15 + x 14 + x 13 + 7 x 12 − 6 x 11 − 6 x 10 + x 9 + 4 x 8 − x 6 + 3 x 5 − 4 x 4 + 4 x 3 + 4 x + 1 e=-3x^{15}+x^{14}+x^{13}+7x^{12}-6x^{11}-6x^{10}+x^9+4x^8-x^6+3x^5-4x^4+4x^3+4x+1 e=−3x15+x14+x13+7x12−6x11−6x10+x9+4x8−x6+3x5−4x4+4x3+4x+1
公钥是由一对多项式组成 p k = ( [ − a s + e ] q , a ) pk=([-as+e]_q,a) pk=([−as+e]q,a),多项式算术取多项式的模,系数算术取 q q q的模。
下面举一个例子,公钥的第一个多项式将这样构建

p k 0 = − 285 x 15 − 431 x 14 − 32 x 13 + 86 x 12 − 83 x 11 − 14 2 10 − 41 x 9 + 430 x 8 + 26 x 7 − 158 x 6 − 281 x 5 + 377 x 4 + 110 x 3 − 234 x 2 − 113 x + 252 pk_0=-285x^{15}-431x^{14}-32x^{13}+86x^{12}-83x^{11}-142^{10}-41x^9+430x^8+26x^7-158x^6-281x^5+377x^4+110x^3-234x^2-113x+252 pk0=−285x15−431x14−32x13+86x12−83x11−14210−41x9+430x8+26x7−158x6−281x5+377x4+110x3−234x2−113x+252
系数取值范围为 { 0 , q − 1 } \{0,q-1\} {0,q−1}的多项式 a a a ,与系数取值范围为 { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1}的多项式 s s s 相乘,由于多项式乘法相对于多项式模数的“旋转和反射”特性,这有效地混合和打乱了 a a a 的所有系数,并且还进一步添加了小误差项 e e e 。多项式 a a a 有效地掩盖了公钥中的私钥 s s s 。
2.2 加密
加密便是将一个多项式且其系数 m o d t mod \ t mod t 的明文,将它转化为一对系数 m o d q mod \ q mod q 的多项式。这里我们举一个例子: m = 3 + 4 x 8 = 3 − 3 x 8 m o d 7 m=3+4x^8=3-3x^8 \ mod \ 7 m=3+4x8=3−3x8 mod 7。
加密需要三个小多项式。两个误差多项式取自与公钥误差多项式相同的离散高斯分布,另一个多项式我们称之为 u u u ,它的系数为 { − 1 , 0 , 1 } \{-1,0,1\} {−1,0,1},就像私钥一样。

密文由两个经计算后的多项式表示:
c
t
=
(
[
p
k
0
u
+
e
1
+
q
m
/
t
]
q
,
[
p
l
1
u
+
e
2
]
q
)
ct=([pk_0u+e_1+qm/t]_q,[pl_1u+e_2]_q)
ct=([pk0u+e1+qm/t]q,[pl1u+e2]q)
消息
m
m
m 是在模
t
t
t 的范围,给它乘上
q
t
\frac{q}{t}
tq 将它的范围缩放到模
q
q
q 上,再加上噪声与掩码。

c
t
0
ct_0
ct0,
c
t
1
ct_1
ct1的计算结果如下,大家没事可以动手算一下。


总之一个密文可以由公钥,私钥,掩码,噪声,消息表示为:

2.3 解密
我们首先通过计算 [ c t 0 + c t 1 s ] q [ct_0+ct_1s]_q [ct0+ct1s]q从消息中完全删除掩码。将计算结果扩展得 [ q m / t + e 1 + e u + e 2 s ] q [qm/t+e_1+eu+e_2s]_q [qm/t+e1+eu+e2s]q,可以看到其中包含缩放后的消息和一些噪声,只要噪声不太大我们便可以通过舍入恢复消息。
 具体来说
具体来说

我们将该多项式重新缩放到模
t
t
t 上,也就是乘上
t
q
\frac{t}{q}
qt :
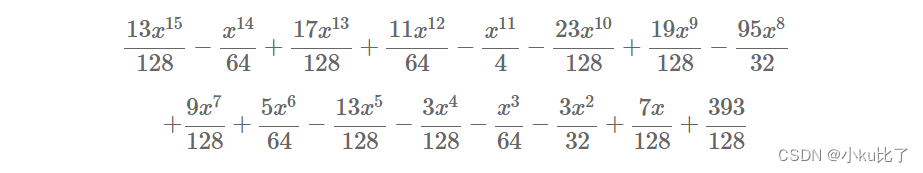
四舍五入这些系数便可以恢复我们的消息:
m
=
3
−
3
x
8
m=3-3x^8
m=3−3x8
我们用下图 来进行说明:在缩放到最接近的整数后,我们将近似系数四舍五入,从而得到我们的信息: 总之,我们通过下式来计算解密结果:
m
′
=
[
⌊
t
q
[
c
t
0
+
c
t
1
s
]
q
⌉
]
t
m^{'}=[\lfloor \frac{t}{q}[ct_0+ct_1s]_q \rceil]_t
m′=[⌊qt[ct0+ct1s]q⌉]t其中
⌊
⌉
\lfloor \rceil
⌊⌉表示取整最接近的整数。
总之,我们通过下式来计算解密结果:
m
′
=
[
⌊
t
q
[
c
t
0
+
c
t
1
s
]
q
⌉
]
t
m^{'}=[\lfloor \frac{t}{q}[ct_0+ct_1s]_q \rceil]_t
m′=[⌊qt[ct0+ct1s]q⌉]t其中
⌊
⌉
\lfloor \rceil
⌊⌉表示取整最接近的整数。
3.同态计算
3.1 同态加法
假设我们有两个多项式 m 1 a n d m 2 m_1 and \ m_2 m1and m2,它们使用相同的公钥加密: a = ( [ p k 0 u 1 + e 1 + q m 1 / t ] q , [ p k 1 u 1 + e 2 ] q ) a=([pk_0u_1+e_1+qm_1/t]_q,[pk_1u_1+e_2]_q) a=([pk0u1+e1+qm1/t]q,[pk1u1+e2]q) b = ( [ p k 0 u 2 + e 3 + q m 2 / t ] q , [ p k 1 u 2 + e 4 ] q ) b=([pk_0u_2+e_3+qm_2/t]_q,[pk_1u_2+e_4]_q) b=([pk0u2+e3+qm2/t]q,[pk1u2+e4]q)我们将a,b相加得到c: c = ( [ p k 0 u 3 + e 5 + q ( m 1 + m 2 ) / t ] q , [ p k 1 u 3 + e 6 ] q ) c=([pk_0u_3+e_5+q(m_1+m_2)/t]_q,[pk_1u_3+e_6]_q) c=([pk0u3+e5+q(m1+m2)/t]q,[pk1u3+e6]q)缩放之前的解密: [ q ( m 1 + m 2 ) / t + e 5 + e u 3 + e 6 s ] q [q(m_1+m_2)/t+e_5+eu_3+e_6s]_q [q(m1+m2)/t+e5+eu3+e6s]q只要最后的噪声不太大,在缩放后被舍入掉,便可以得到正确的解密结果。
3.2 同态乘法
首先我们根据同态的解密公式得: [ c t 0 + c t 1 s 1 ] q [ct_0+ct_1s^1]_q [ct0+ct1s1]q注意:这个方程是一个多项式 ( c t 0 ) (ct_0) (ct0)乘以1( s 0 s^0 s0)加上一个多项式 ( c t 1 ) (ct_1) (ct1)乘以另一个多项式 ( s 1 ) (s^1) (s1),然后对 x d + 1 x^d+1 xd+1 取模,对 q q q 取模。
现在,我们在上面看到解密产生了一个独立于掩码项
a
u
au
au 的量
n
o
i
s
e
noise
noise
[
c
t
0
+
c
t
1
s
1
]
q
→
t
q
m
+
n
o
i
s
e
[ct_0+ct_1s^1]_q \rightarrow \frac{t}{q}m+noise
[ct0+ct1s1]q→qtm+noise
我们现在考虑两个多项式
m
1
a
n
d
m
2
m_1 and \ m_2
m1and m2 使用相同的公钥加密:
[
a
0
+
a
1
s
1
]
q
→
t
q
m
1
+
n
1
[a_0+a_1s^1]_q \rightarrow \frac{t}{q}m_1+n_1
[a0+a1s1]q→qtm1+n1
[
b
0
+
1
s
1
]
q
→
t
q
m
2
+
n
2
[b_0+_1s^1]_q \rightarrow \frac{t}{q}m_2+n_2
[b0+1s1]q→qtm2+n2
如果我们取它们的乘积,我们有:
[
a
0
+
a
1
s
1
]
q
[
b
0
+
1
s
1
]
q
→
(
t
q
m
1
+
n
1
)
(
t
q
m
2
+
n
2
)
[a_0+a_1s^1]_q[b_0+_1s^1]_q \rightarrow (\frac{t}{q}m_1+n_1)(\frac{t}{q}m_2+n_2)
[a0+a1s1]q[b0+1s1]q→(qtm1+n1)(qtm2+n2)
我们将左边展开:
m
u
l
t
(
a
,
b
)
=
c
0
+
c
1
s
+
c
2
s
2
mult(a,b)=c_0+c_1s+c_2s^2
mult(a,b)=c0+c1s+c2s2其中
c
0
=
[
t
q
a
0
b
0
]
q
c_0=[\frac{t}{q}a_0b_0]_q
c0=[qta0b0]q
c
1
=
[
t
q
(
a
1
b
0
+
a
0
b
1
)
]
q
c_1=[\frac{t}{q}(a_1b_0+a_0b_1)]_q
c1=[qt(a1b0+a0b1)]q
c
2
=
[
t
q
a
1
b
1
]
q
c_2=[\frac{t}{q}a_1b_1]_q
c2=[qta1b1]q
最后的公式应该为:
m
u
l
t
(
a
,
b
)
=
[
⌊
t
q
[
c
0
+
c
1
s
+
c
2
s
2
]
⌉
]
t
mult(a,b)=[\lfloor \frac{t}{q}[c_0+c_1s+c_2s^2]\rceil]_t
mult(a,b)=[⌊qt[c0+c1s+c2s2]⌉]t
英文链接