力扣爆刷第127天之动态规划五连刷(整数拆分、一和零、背包)
文章目录
- 力扣爆刷第127天之动态规划五连刷(整数拆分、一和零、背包)
- 关于0 1 背包问题的总结
- 01背包遍历顺序:
- 完全背包遍历顺序:
- 一、343. 整数拆分
- 二、96. 不同的二叉搜索树
- 三、416. 分割等和子集
- 四、1049. 最后一块石头的重量 II
- 五、494. 目标和
关于0 1 背包问题的总结
背包问题:一维数组,dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i])。
01背包遍历顺序:
先物品后背包,物品正序,背包逆序。
如若背包正序则会出现同一个物品重复放入,如物品1重量为1,背包空间为1时放入了,背包空间为2时又放入了。
如果先背包后物品,为了避免重复放入背包依然是逆序,背包容量固定时,每种背包容量只能放入一个物品,即为最大的物品,小的物品都放不进来或者被覆盖了。
求组合数排列数:dp[j] += dp[j - nums[i]]
完全背包遍历顺序:
物品背包没有先后顺序,物品背包都是正序。因为同一个物品不限量可以放入多次,在背包采用正序中。
完全背包求组合数,物品在外,背包在内。求排列数,背包在外,物品在内。
一、343. 整数拆分
题目链接:https://leetcode.cn/problems/integer-break/description/
思路:整数拆分是把整数拆分成k个数使其乘积最大,最低是拆分成两个数,根据题目要求的目标定义dp[i]表示i被拆分后相乘的最大值,对于任意一个数来说,最低是拆分成两个数,然后就是两个数以上,我们要求的就是这些情况中的最大值,显然发现是有状态转移的关系的,如dp[i],如果拆分成两个数,那就是(i-j)* j,如果拆分成两个数以上就是dp[i-j] * j,每一个数都要遍历这些情况,故 dp[i] = Math.max(Math.max(dp[i-j] * j, (i-j)*j), dp[i]);
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i <= n; i++) {
for(int j = 1; j <= i/2; j++) {
dp[i] = Math.max(Math.max(dp[i-j] * j, (i-j)*j), dp[i]);
}
}
return dp[n];
}
}
二、96. 不同的二叉搜索树
题目链接:https://leetcode.cn/problems/unique-binary-search-trees/
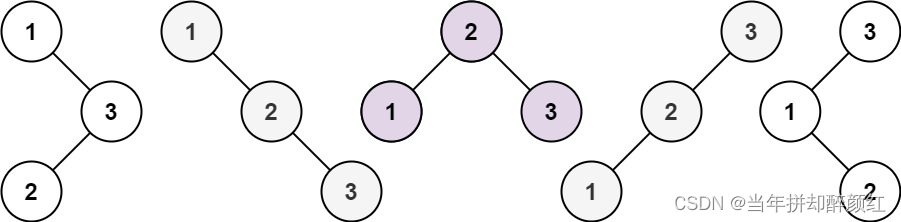
思路:做动态规划的题目主要是找出重叠子问题,推导出状态转移方程,定义dp[i]表示i个节点的二叉搜索树有多少种结构类型,dp[3]也就是有3个节点我们可以看出,1为根节点有两种,2为根节点有1种,3为根节点有2种,但1为根节点时,右子树有两个节点,这2个节点的种类数量其实是和dp[2]是一样的,由此我们是可以看出关系来的,有N个节点的二叉搜索树的类型数量就等于1-N每一个数字作为根节点时种类数量的累加,这里正好有重叠子问题。故递推公式为dp[i] += dp[j-1] * dp[i-j];
以dp[3]推导举例:
1为根节点,dp[0]*dp[2]。
2为根节点,dp[1]*dp[1]。
3为根节点,dp[2]*dp[0]。这里是有复用关系的。
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= i; j++) {
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
}
三、416. 分割等和子集
题目链接:https://leetcode.cn/problems/partition-equal-subset-sum/description/
思路:0 1背包问题,划分等和子集,如果和为偶数就可以划分,奇数就不能划分。偶数可以划分,就等于用数组里的数把总和的一半给填满,那么就可以划分等和子集,从而转化为0 1 背包问题。
0 1 背包特点,物品在外,背包在内,背包逆序。内外关系为的是防止,大物品放入后,小物品无法再放入。背包逆序为的是防止物品重复放入。
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for(int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if(sum % 2 == 1) return false;
sum /= 2;
int[] dp = new int[sum+1];
for(int i = 0; i < nums.length; i++) {
for(int j = sum; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);
}
}
return dp[sum] == sum;
}
}
四、1049. 最后一块石头的重量 II
题目链接:https://leetcode.cn/problems/last-stone-weight-ii/description/
思路:求最后一块是否的重量,就是两两抵消,求最后剩余的无法抵消的数,转换思路想一想其实就是尽量把石头分成两堆大小接近的堆,然后比较最小差值,所以题目就转变成了0 1背包问题,总数和的一半作为背包,求的结果后,乘2与总数相减即得最后一块是否的重量。
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0, total = 0;
for(int i = 0; i < stones.length; i++) {
total += stones[i];
}
sum = total / 2;
int[] dp = new int[sum+1];
for(int i = 0; i < stones.length; i++) {
for(int j = sum; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return total - dp[sum] * 2;
}
}
五、494. 目标和
题目链接:https://leetcode.cn/problems/target-sum/description/
思路:0 1 背包求组合数,想办法转化为背包,得到背包空间,因为分为正数和负数,a + b = sum; a - b = target。
a = (sum+target) / 2;
由此可以得到正数背包,从而转变从背包求组合数,定义dp[j]表示,背包空间为j时的物品组合数,那么自然,递推公式为dp[j] += dp[j - nums[i]]; 所以需要初始化为1.
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for(int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if(sum < Math.abs(target) || (sum + target) % 2 == 1) return 0;
int left = Math.abs((sum + target) / 2);
int[] dp = new int[left+1];
dp[0] = 1;
for(int i = 0; i < nums.length; i++) {
for(int j = left; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[left];
}
}