本篇博客主要介绍一下什么是线段树与树状数组,它们的原理与结构是怎样,并通过实际题型来讲解,篇一主要讲解线段树,下一篇博客讲解树状数组。
线段树与树状数组的区别和特点:
它们的时间复杂度都是O(nlogn)
- 存储方式和空间复杂度不同。线段树使用树形结构存储,其空间复杂度通常较高;树状数组使用数组存储,空间复杂度较低。
- 操作复杂度不同。线段树和树状数组在操作复杂度上有所差异,线段树的查询和更新操作的时间复杂度通常为O(log n)或O(log^2 n),而树状数组的查询和更新操作的时间复杂度为O(log n)。
- 应用场景不同。线段树适用于区间修改、区间查询的场景;树状数组适用于单点修改、区间查询的场景。
- 功能不同。线段树可以维护区间信息,包括区间和、最大值、最小值等;树状数组主要维护前缀和,通过特定操作也可以实现区间查询,但功能上不如线段树强大。
总体来说,线段树的构造更难一些,但是功能很强,树状数组的实现较简单,但功能较弱
什么是线段树?
自己写了半天的博客发现还是水平有限,介绍的知识点不太全面,这里引用一篇其他博主的线段树介绍什么是线段树,介绍的内容很细也很好理解。
这里说明一下问什么要开4n倍的数组空间:
设最后有n个叶结点,对应的满二叉树最多有2n个叶结点(这是因为极端情况是倒数第二层区间长度1,2交替) 然后根据(2n)+n+n/2…<=4n
下面结合具体题目来看看如何用线段树解决实际问题。
题目: 动态求连续区间和
题目链接:1264. 动态求连续区间和
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b]
的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n,
数据保证在任何时候,数列中所有元素之和均在 int 范围内。
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35
思路:
题目描述很简单,看数据范围是 1 0 5 10^5 105,如果每次都要遍历数组再查询的话时间复杂度为O( n 2 n^2 n2),也就是 1 0 10 10^{10} 1010,明显超时。所以需要把时间复杂度降到O(logn),而题目中涉及的操作只有区间修改和区间查询,线段树的模板题。
首先需要构建线段树,每个节点有3个值,左区间,右区间,区间总和值
class Node:
def __init__(self):
# 左右区间与总和
self.l, self.r, self.sum = 0, 0, 0
构造线段树其实就是数据结构中构造树的过程
def push_up(u): # 利用它的两个儿子来算一下它的当前节点信息
# 左儿子 u * 2 ,右儿子 u * 2 + 1
tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum
def build(u, l, r): # 第一个参数:当前节点编号。第二个参数:左边界。第三个参数:右边界。
if l == r: # 如果当前已经是叶节点了,那我们就直接赋值就可以了
tr[u].l, tr[u].r, tr[u].sum = l, r, val[r]
# 否则的话,说明当前区间长度至少是 2 对吧,那么我们需要把当前区间分为左右两个区间,那先要找边界点
else:
tr[u].l, tr[u].r = l, r # 这里记得赋值一下左右边界的初值
mid = (l + r) // 2 # 边界的话直接去计算一下 l + r 的下取整
build(u * 2, l, mid) # 先递归一下左儿子
build(u * 2 + 1, mid + 1, r) # 然后递归一下右儿子
push_up(u) # 做完两个儿子之后的话呢 push_up 一遍u ,更新一下当前节点信息
build(1, 1, n) # 第一个参数是根节点的下标,根节点是一号点,然后初始区间是 1 到 n
如样例所示线段树图示:
区间 [1,10]
数列值为 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ]
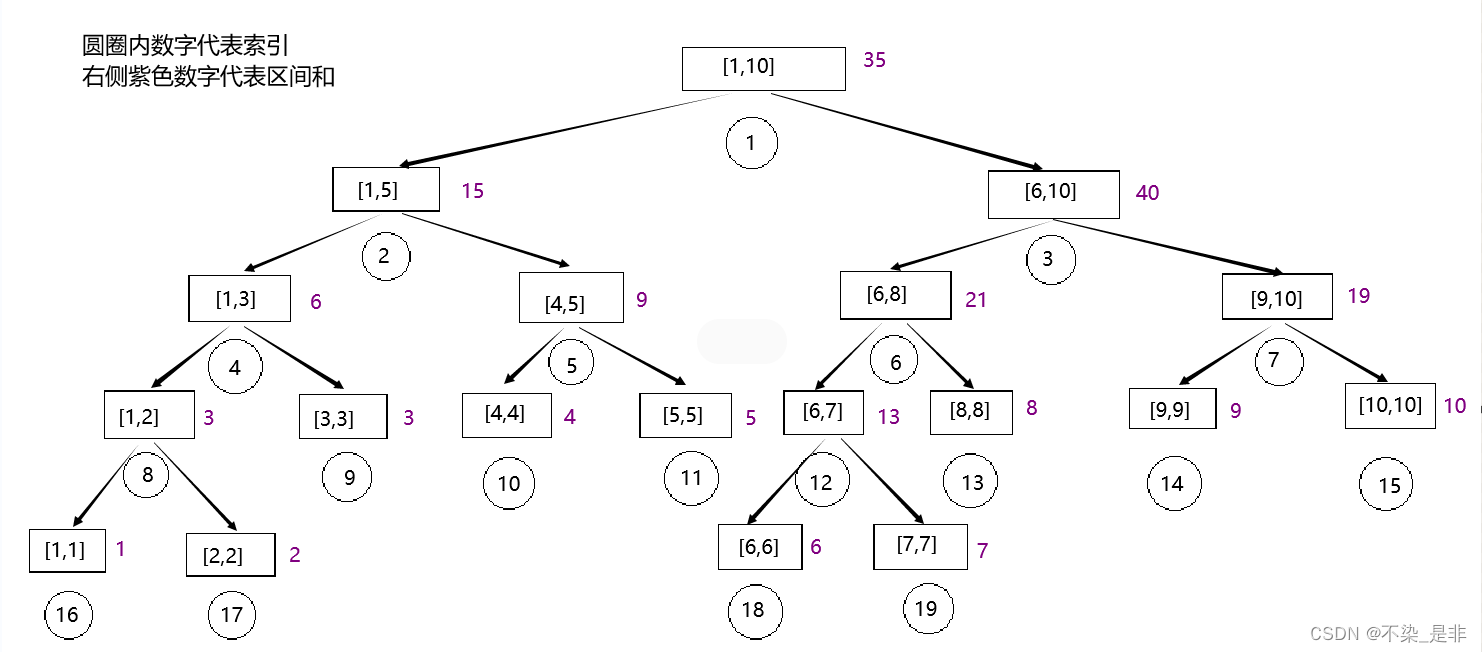
线段树构造好之后就要进行修改和查询操作了,这里的查询无需用到 lazy 标记,因为它不是修改完所有数值之后才进行查询操作,而是修改和查询操作随时都会进行不分先后顺序。
查询操作:
def query(u, l, r): # 查询的过程是从根结点开始往下找对应的一个区间
if tr[u].l >= l and tr[u].r <= r: # 如果当前区间已经完全被包含了,那么我们直接返回它的值就可以了
return tr[u].sum
# 否则的话我们需要去递归来算
else:
mid = (tr[u].l + tr[u].r) // 2 # 计算一下我们 当前 区间的中点是多少
total_sum = 0 # 用 total_sum 来表示一下我们的总和
if mid >= l: # 看一下我们当前区间的中点和左边有没有交集
total_sum += query(u * 2, l, r)
if mid + 1 <= r: # 看一下我们当前区间的中点和右边有没有交集
total_sum += query(u * 2 + 1, l, r)
return total_sum
这里有两处稍微绕一点:
- 查询区间和时,为什么当前区间被完全包含就返回它的值?
- 查询区间和时,为什么要判断跟左bb右边有无交集?
这里举个例子求一下就可以明白
我们在查询时,查询的过程是从根结点开始往下找对应的一个区间,如果要查找的区间是根节点区间,直接返回,否则第一次递归之前是不可能有区间完全包含根节点区间,拿样例结合上图图示说明,l 和 r 的取值范围就在 1 ~ 10 之间,不可能小于1 也不可能大于 10。
只要不是根节点区间查询区间和,那么就会进行到下一步。比如查询区间 [1, 8] 的和,因为查询区间不完全包含根节点区间,所以需要判断根节点区间的中点跟查询区间左右两边是否有交集。
根节点区间的中点为5,所以查询区间 [1, 8] 跟左右两边都有交集,所以总和total_sum 需要加上跟左右两边交集的和(也就是要加上[1,5] 和 [6,8]的和)。
先加左半边交集的和,递归到左孩子节点(下标索引为2的节点),因为[1, 8] 完全包含[1,5] 所以直接返回 区间[1,5] 的和(和是15)。
再加右半边交集的和,继续判断,直到可以求出[6,8] 的和为止。
修改操作:
def modify(u, index, v): # 第一个参数也就是当前节点的编号,第二个参数是要修改的位置,第三个参数是要修改的值
if tr[u].l == tr[u].r: # 如果当前已经是叶节点了,那我们就直接让他的总和加上 v 就可以了
tr[u].sum += v
else:
mid = (tr[u].l + tr[u].r) // 2
# 看一下 index 是在左半边还是在右半边
if index <= mid: # 如果是在左半边,那就找左儿子
modify(u * 2, index, v)
else: # 如果在右半边,那就找右儿子
modify(u * 2 + 1, index, v)
# 更新完之后当前节点的信息就要发生变化对吧,那么我们就需要 push_up 一遍
push_up(u)
以上就是线段树的所有操作,就是按照线段树的概念来构成的,理解了线段树的概念也就会做本题了。
完整代码及注释:
class Node:
def __init__(self):
# 左右区间与总和
self.l, self.r, self.sum = 0, 0, 0
def push_up(u): # 利用它的两个儿子来算一下它的当前节点信息
# 左儿子 u * 2 ,右儿子 u * 2 + 1
tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum
def build(u, l, r): # 第一个参数:当前节点编号。第二个参数:左边界。第三个参数:右边界。
if l == r: # 如果当前已经是叶节点了,那我们就直接赋值就可以了
tr[u].l, tr[u].r, tr[u].sum = l, r, val[r]
# 否则的话,说明当前区间长度至少是 2 对吧,那么我们需要把当前区间分为左右两个区间,那先要找边界点
else:
tr[u].l, tr[u].r = l, r # 这里记得赋值一下左右边界的初值
mid = (l + r) // 2 # 边界的话直接去计算一下 l + r 的下取整
build(u * 2, l, mid) # 先递归一下左儿子
build(u * 2 + 1, mid + 1, r) # 然后递归一下右儿子
push_up(u) # 做完两个儿子之后的话呢 push_up 一遍u ,更新一下当前节点信息
def query(u, l, r): # 查询的过程是从根结点开始往下找对应的一个区间
if tr[u].l >= l and tr[u].r <= r: # 如果当前区间已经完全被包含了,那么我们直接返回它的值就可以了
return tr[u].sum
# 否则的话我们需要去递归来算
else:
mid = (tr[u].l + tr[u].r) // 2 # 计算一下我们 当前 区间的中点是多少
total_sum = 0 # 用 total_sum 来表示一下我们的总和
if mid >= l: # 看一下我们当前区间的中点和左边有没有交集
total_sum += query(u * 2, l, r)
if mid + 1 <= r: # 看一下我们当前区间的中点和右边有没有交集
total_sum += query(u * 2 + 1, l, r)
return total_sum
def modify(u, index, v): # 第一个参数也就是当前节点的编号,第二个参数是要修改的位置,第三个参数是要修改的值
if tr[u].l == tr[u].r: # 如果当前已经是叶节点了,那我们就直接让他的总和加上 v 就可以了
tr[u].sum += v
else:
mid = (tr[u].l + tr[u].r) // 2
# 看一下 index 是在左半边还是在右半边
if index <= mid: # 如果是在左半边,那就找左儿子
modify(u * 2, index, v)
else: # 如果在右半边,那就找右儿子
modify(u * 2 + 1, index, v)
# 更新完之后当前节点的信息就要发生变化对吧,那么我们就需要 push_up 一遍
push_up(u)
n, m = map(int, input().split())
val = list(map(int, input().split()))
val = [0, *val] # 记录一下权重
tr = [Node() for _ in range(4 * n + 10)] # 记得开 4 倍空间,防止爆栈
build(1, 1, n) # 第一个参数是根节点的下标,根节点是一号点,然后初始区间是 1 到 n
for _ in range(m):
k, a, b = map(int, input().split())
if k == 0:
print(query(1, a, b)) # 求和的时候,也是传三个参数,第一个的话是根节点的编号 ,第二和第三个的话是我们查询的区间
else:
modify(1, a, b) # 第一个参数是根节点的下标,第二个参数是要修改的位置,第三个参数是要修改的值
总结:
没接触线段树前还觉得线段树很难实现和理解,但其实把线段树的概念原理理解了就会发现线段树还是比较简单的(就是不太好构造,树形结构肯定不如普通数组好构造)。下一篇博客将讲解树状数组。