1:事实表和维表的概述
前言:数据仓库是一种用于存储和管理大量数据的技术。其中,事实表和维表是数据仓库中的两个重要概念,首先了解一下事实表和维度表
1.事实表:是指用于存储测量“事实数据”的表,事实数据表包含描述业务(例如产品销售)内特定事件的数据,例如订单信息表、销售记录表等
2.维表是用于提供事实表上下文和维度信息的表,例如时间表、地区表、客户表等
事实表通常包含多个维表,这些维表提供了与事实数据相关的上下文和维度信息,维表通常与事实表相关联,以提供关于数据测量的上下文和描述信息。
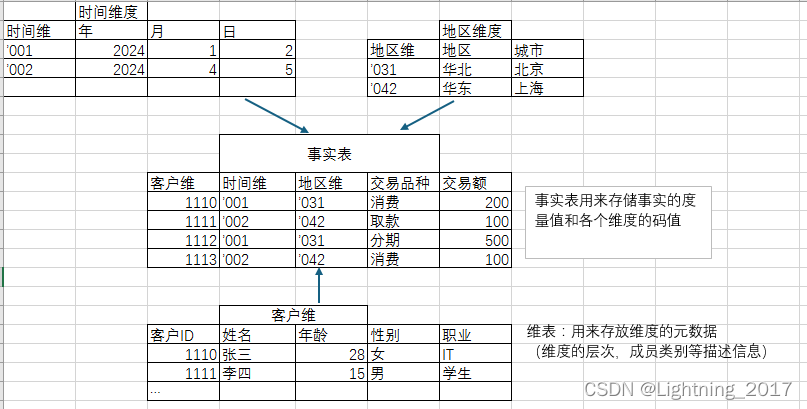
以上总结:
1.事实表存储的是度量值,也可以是计算值,是一条一条的明细,可分为周期快照事实表(按一定的周期业务积累的数据)和累计快照事实表(记录整个过程的数据)
2.维度表:由上图可看,维度表一般都是每条数据都是唯一的,有主键设置,它的主键是事实表的外键。可细分一般维度表(数据是不断增加和变化的)和固定维度表(数据是不变的,例如码值表)
2.数据模型
数据模型一般分为:星型模型、雪花模型、星型-雪花模型、事实星座模型
一、星型模型
星型模型是由一个事实表和多个维度表组成的一种体系结构。事实表位于星型模型的中心,维度表则呈辐射状与事实表相连,各种维度表之间不存在联系。这种模型的结构简单,易于理解和实现。此外,星型模型还具有较好的查询性能和可扩展性,因此在数据仓库的构建中被广泛采用。
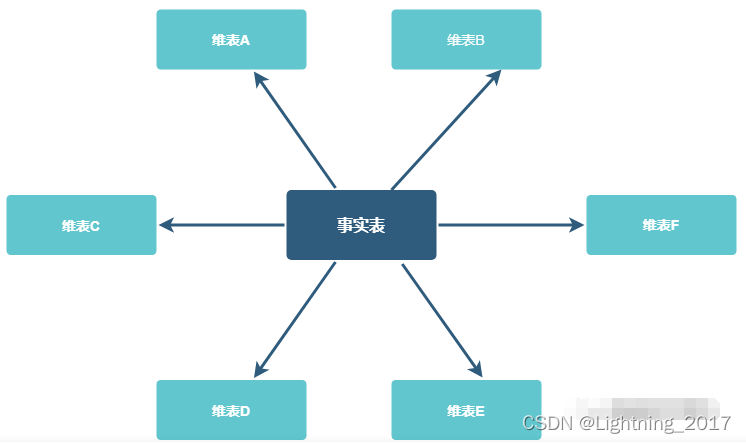
二、雪花模型
雪花模型是由1个事实表和多个维度表组成的一种体系结构。维度表和维表相连,再连接到事实表,形成一个复杂的网状结构。与星型模型相比,雪花模型的结构更加灵活,能够更好地支持复杂的数据分析需求。然而,这种模型的构建和维护较为困难,且查询性能相对较低。
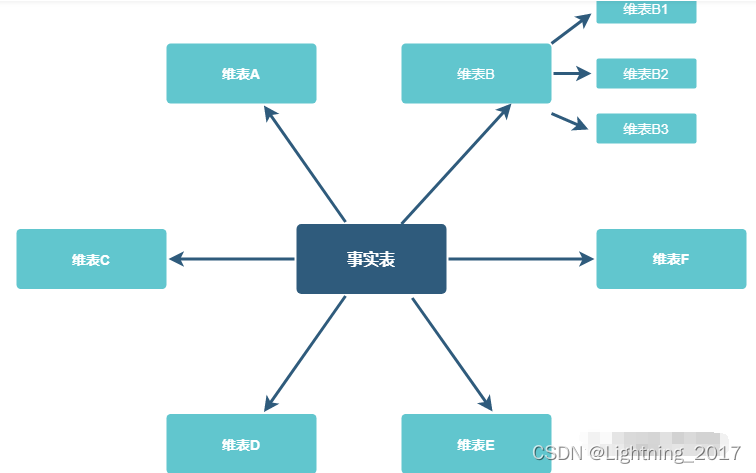
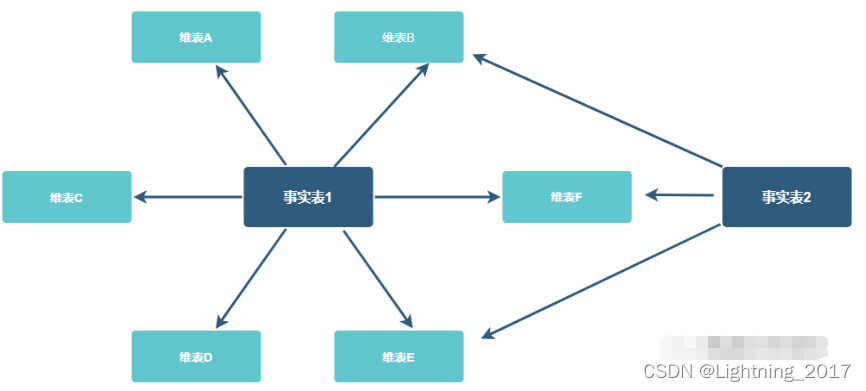
三、事实星座模型
事实星座模型是由多个事实表和多个维度表组成的一种体系结构。与雪花模型不同的是,事实星座模型的事实表之间不再直接相连,而是通过维度表相连形成一个星座状结构。这种模型的结构非常灵活,能够更好地支持复杂的数据分析需求。然而,这种模型的构建和维护非常困难,需要谨慎使用。
3.维度建模四个步骤
1.选择业务过程
表示的是业务执行的活动,产生一系列事实表。
2.声明粒度
粒度是事实表的度量细节级别。通常从原子级别粒度开始设计,这样可以支持上卷,也支持下钻细节,能够承受各种用户查询。
3.确认维度
文本属性,用来修饰事实表。
4.确认事实
是维度建模的核心。
不同粒度的度量要放在不同的事实表中。
通过外键关联相关维度。
查询操作是基于事实表开展计算和聚合





![[x86] OpenBMC简介](https://img-blog.csdnimg.cn/direct/5f7f83bdb0f844beb02c90c8dc08d873.jpeg)