2. 认识O(logN)的排序

news2025/1/16 3:47:46

1. 递归

  • 递归arr[L…R]范围上求最大值
    流程分析如下:
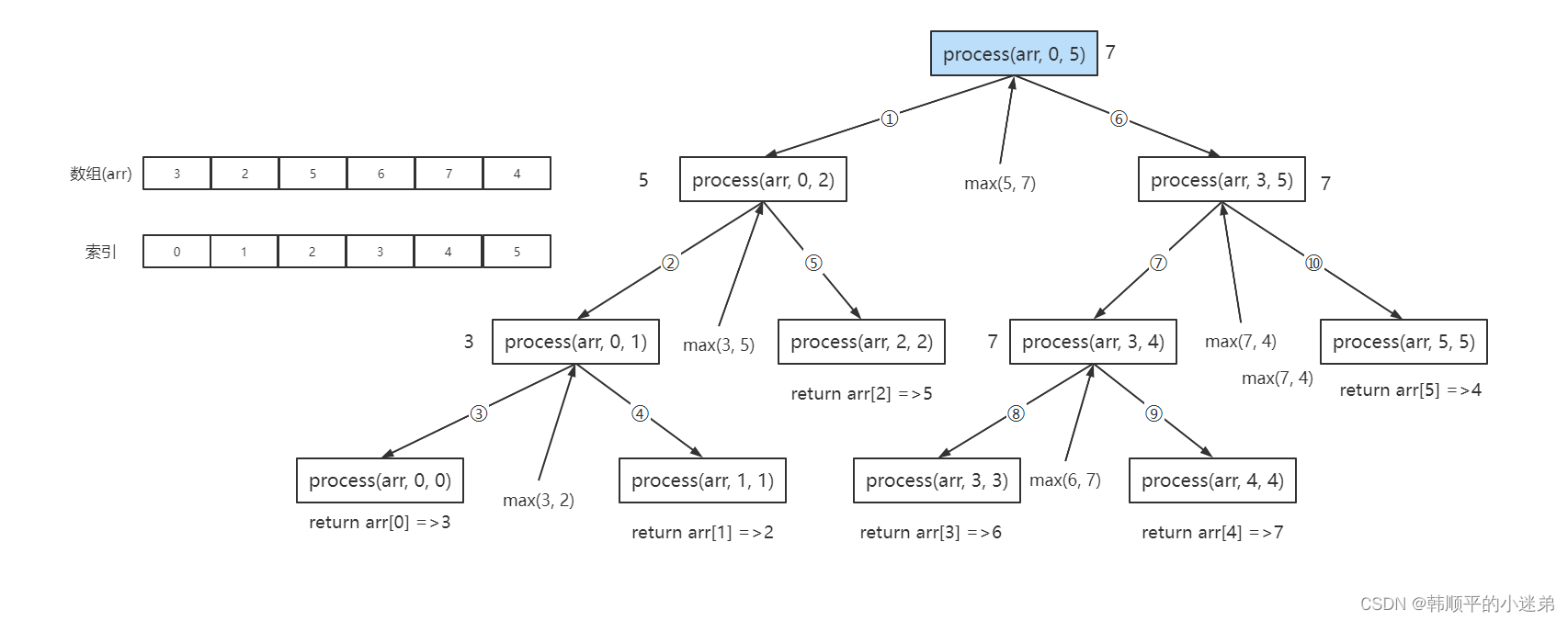
    在这里插入图片描述
    java代码:
package paixu.class01;

public class Code08_GetMax {
    public static void main(String[] args) {
        int[] arr = {3,2,5,6,7,4};
        System.out.println(getMax(arr));
    }

    public static int getMax(int[] arr) {
        return process(arr, 0, arr.length - 1);
    }

    //arr[L..R]范围上求最大值
    public static int process(int[] arr, int L, int R) {
        if (L == R){ //arr[L..R]范围上只有一个数，直接返回
            return arr[L];
        }
        int mid = L + ((R-L) >> 1);
        int leftMax = process(arr, L, mid);
        int rightMax = process(arr, mid + 1, R);
        return Math.max(leftMax, rightMax);
    }
}

在这里插入图片描述

2. Master公式

Master公式用来计算子问题规模确定的递归函数的时间复杂度。

master公式的使用
T(N) = a*T(N/b) + O(N^d)

  1. log(b,a) > d ->复杂度为O(N^log(b,a))
  2. log(b,a) = d -> 复杂度为O(N^d * logN)
  3. log(b,a) < d -> 复杂度为O(N^d)

说明：
T(N)：母问题的规模
T(N/b)： 子问题的规模
a： 子问题调用次数
O(N^d)：除了子问题之外，其他逻辑的时间复杂度

例子: 上面递归求arr[L…R]范围上最大值。满足master公式。
T(N) = 2*T(N/2) + O(N^0)

3. 归并排序

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。
归并排序时间复杂度O(N*logN)，额外空间复杂度O(N),稳定排序
归并操作，也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法。归并排序的流程图如下:
在这里插入图片描述
在看归并排序时，我们首先要能够归并两个有序数组，换句话说就是合并两个有序数组为一个有序数组。
例如归并以下两个数组。素材来源 https://blog.csdn.net/weixin_50941083/article/details/120852477

a[5] = {3，5，7，8，10}
b[7] = {1，2，4，5，8，11，1}

主要思想：

  1. 定义一个新数组c，可以容纳a和b两个数组中的所有元素；
  2. 初始化三个下标（都指向第一个元素），i给a数组，j给b数组，k是新数组c的；
  3. a[i]和b[j]进行比较：若a[i]<b[j]，将a[i]填入c[k]，i++，k++；若a[i]>b[j]，将b[j]填入c[k]，j++，k++;
  4. 循环第三步，直至其中一个数组中的数据全部填入数组c中，再将另外一个还有剩余的数组中的元素放入新数组c中。

图解过程如下：
在这里插入图片描述
java代码:

package paixu.class02;

import java.util.Arrays;

public class Code01_MergeSort_ {
    public static void main(String[] args) {
        int[] arr = {10,4,6,3,8,2,5,7};
        mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void mergeSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        process(arr, 0, arr.length - 1);
    }

    public static void merge(int[] arr, int l, int m, int r) {
        int[] tempArr = new int[r - l + 1];
        int i = l;
        int j = m + 1;
        int k = 0;
        while (i <= m && j <= r) {
            if (arr[i] <= arr[j]) {
                tempArr[k++] = arr[i++];
            }else{
                tempArr[k++] = arr[j++];
            }
        }
        while (i <= m) {
            tempArr[k++] = arr[i++];
        }
        while (j <= r) {
            tempArr[k++] = arr[j++];
        }

        //把临时保存数组数据拷贝到原数组
        for (int e = 0; e < tempArr.length; e++) {
            arr[l++] = tempArr[e];
        }
    }

    public static void process(int[] arr, int L, int R) {
        if (L == R) {
            return;
        }
        int mid = L + ((R - L) >> 1);
        process(arr, L, mid);
        process(arr, mid + 1, R);
        merge(arr, L, mid, R);
    }
}

在这里插入图片描述
master公式分析归并排序:
merge()的时间复杂度为O(N)
T(N) = 2T(N/2) + O(N) -> a = 2, b = 2, d = 1
log(b,a) = d -> 时间复杂度为O(N * logN)

1. 小和问题

参考 https://blog.csdn.net/qq_37236745/article/details/83625679
描述
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例子
[1,3,4,2,5]
1左边比1小的数：没有
3左边比3小的数：1
4左边比4小的数：1,3
2左边比2小的数：1
5左边比5小的数：1,3,4,2
所以小和为1+1+3+1+1+3+4+2=16
解题思路
如果直接用两层for循环扫，时间复杂度是O(n ^2) ，但是可以通过归并排序的方法将时间复杂度降到O(nlogn)
具体做法：归并排序分两步，一是分，二是治。分好说，不停的将数组划分为两部分，比如样例，最终划分为如下图所示的样子
在这里插入图片描述
分完以后开始治，归并排序的治就是merge的过程，首先对1和3进行merge，在此过程中产生一个小和1；然后将1、3和4进行merge，在此过程中产生小和1、3；然后2和5进行merge，产生小和2；最后将1、3、4和2、5进行一次merge，1比2小，所以一共产生n个1的小和，这个n就是当前右边的数的个数，因为右边有两个数2和5，所以产生2个1的小和，然后将1填入辅助数组，继续比较3和2，2比3小，但是2是右边的数，所以不算小和，然后比较3和5，3比5小，所以产生n个3的小和，因为右侧只有一个数，所以就只产生1个3的小和，同样的，
产生1个4的小和
这道题换个角度来想，题目要求的是每个数左边有哪些数比自己小，其实不就是右边有多少个数比自己大，那么产生的小和就是当前值乘以多少个吗？还是以上面的样例举例，1右边有4个比1大的数，所以产生小和14；3右边有2个比3大的数，所以产生小和32；4右边有一个比4大的数，所以产生小和41；2右边没有比2大的数，所以产生小和为20；5右边也没有比5大的数，所以产生小和5*0

java代码:

package paixu.class02;


public class Code02_SmallSum {
    public static void main(String[] args) {
        int[] arr = {1,3,4,2,5};
        System.out.println(getSmallSum(arr));
    }
    public static int getSmallSum(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return 0;
        }
        return process(arr, 0, arr.length - 1);
    }
    public static int merge(int[] arr, int l, int m, int r) {
        int res = 0;
        int[] tempArr = new int[r - l + 1];
        int i = l;
        int j = m + 1;
        int k = 0;
        while (i <= m && j <= r) {
            if (arr[i] < arr[j]) {
                res += arr[i] * (r - j + 1);
                tempArr[k++] = arr[i++];
            }else{
                tempArr[k++] = arr[j++];
            }
        }
        while (i <= m) {
            tempArr[k++] = arr[i++];
        }
        while (j <= r) {
            tempArr[k++] = arr[j++];
        }
        //临时数组拷贝到原数组
        for (int e = 0; e < tempArr.length; e++) {
            arr[l++] = tempArr[e];
        }
        return res;
    }

    public static int process(int[] arr, int L, int R) {
        if (L == R) {
            return 0;
        }
        int mid = L + ((R - L) >> 1);
        return process(arr, L, mid) + process(arr, mid + 1, R) + merge(arr, L, mid, R);
    }
}

在这里插入图片描述

2. 逆序对

  • 什么是逆序对呢？百度百科这样解释：

设 A 为一个有 n 个数字的有序集 (n>1)，其中所有数字各不相同。如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对，也称作逆序数。

  • 在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有逆序对，或者逆序对数量?

分析：
本题其实就是统计数组中右边比左边小的数据对数。用归并排序算法的思想
java代码:

package paixu.class02;

public class Code03_nixudui_ {
    public static void main(String[] args) {
        int[] arr = {3,2,4,5,0};
        int res = getNixuNum(arr);
        System.out.println(res);
    }
    public static int getNixuNum(int[] arr) {
        if (arr == null || arr.length < 1) {
            return 0;
        }
        return process(arr, 0, arr.length - 1);
    }

    public static int merge(int[] arr, int l, int mid, int r) {
        int res = 0;
        int i = l;
        int j = mid + 1;
        int k = 0;
        int[] tempArr = new int[r - l + 1];
        while (i <= mid && j <= r) {
            if (arr[i] > arr[j]) {
                res += (r - j + 1);
                for (int g = j; g <= r; g++) {
                    System.out.println(arr[i] + " -> " + arr[g]);
                }
                tempArr[k++] = arr[i++];
            }else {
                tempArr[k++] = arr[j++];
            }
        }
        while (i <= mid) {
            tempArr[k++] = arr[i++];
        }
        while (j <= r) {
            tempArr[k++] = arr[j++];
        }
        for (int e = 0; e < tempArr.length; e++) {
            arr[l++] = tempArr[e];
        }
        return res;
    }

    public static int process(int[] arr, int l, int r) {
        if (l == r) {
            return 0;
        }
        int mid = l + ((r - l) >> 1);
        int left = process(arr, l, mid);
        int right = process(arr, mid + 1, r);
        int merge = merge(arr, l, mid, r);
        return  left + right + merge;
    }
}

在这里插入图片描述

4. 快速排序

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

(1)首先设定一个分界值，通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于分界值，而右边部分中各元素都大于或等于分界值。
(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

排序步骤
原理：
设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它左边，所有比它大的数都放到它右边，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

荷兰国旗问题
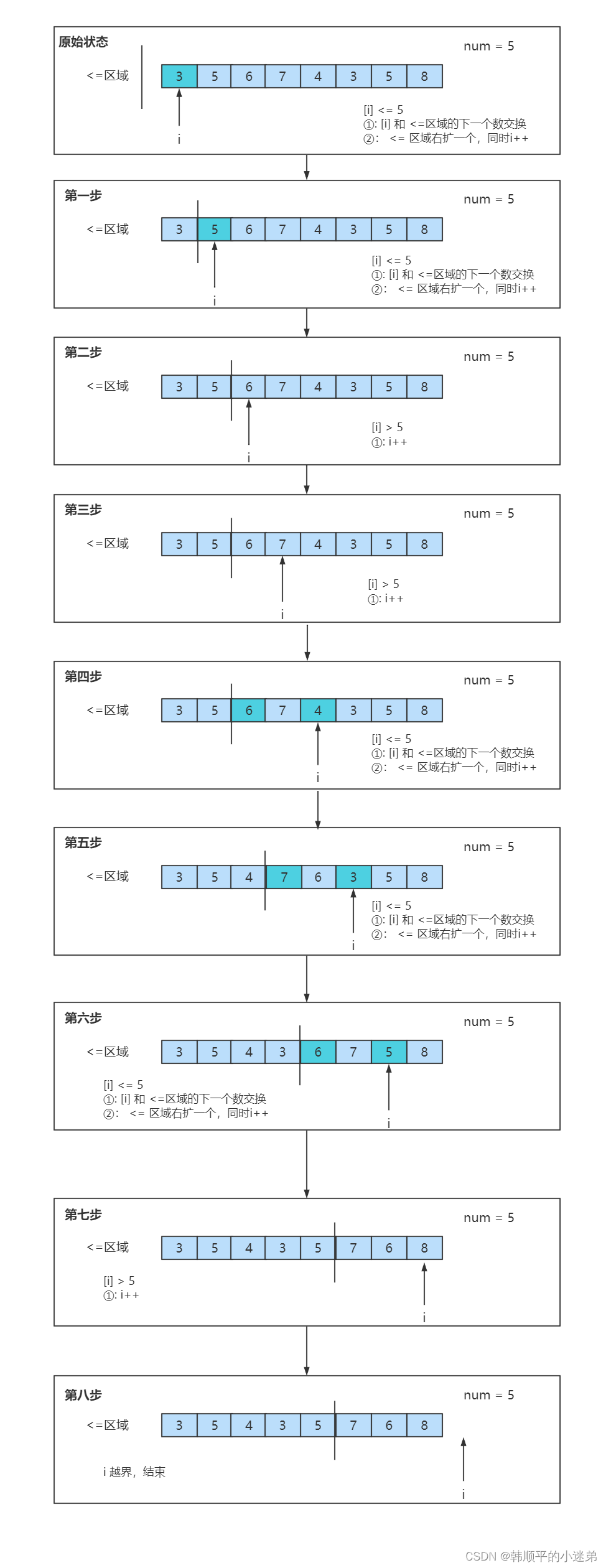
问题一：给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)
解决方案:
划定一个<=区域 j，初始化为-1，一个指针i 初始化指向arr[0],arr[i]与num比较大小:

  1. arr[i] <= num;arr[i] 和 <=区域的下一个数交换， <=区域右扩一个（j++），同时 i++; 2)arr[i]
  2. arr[i] > num; i++;

例子:arr = [3,5,6,7,4,3,5,8], num = 5。整个流程如下:
在这里插入图片描述
java代码:

//在数组arr中，把小于num的数放在数组左边，大于num的数放在右边
    public static void version1(int[] arr, int num) {
        int leftArea = -1;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] <= num) {
                swap(arr, i, ++leftArea);
            }
        }
        System.out.println(leftArea);
    }

问题二(荷兰国旗问题)
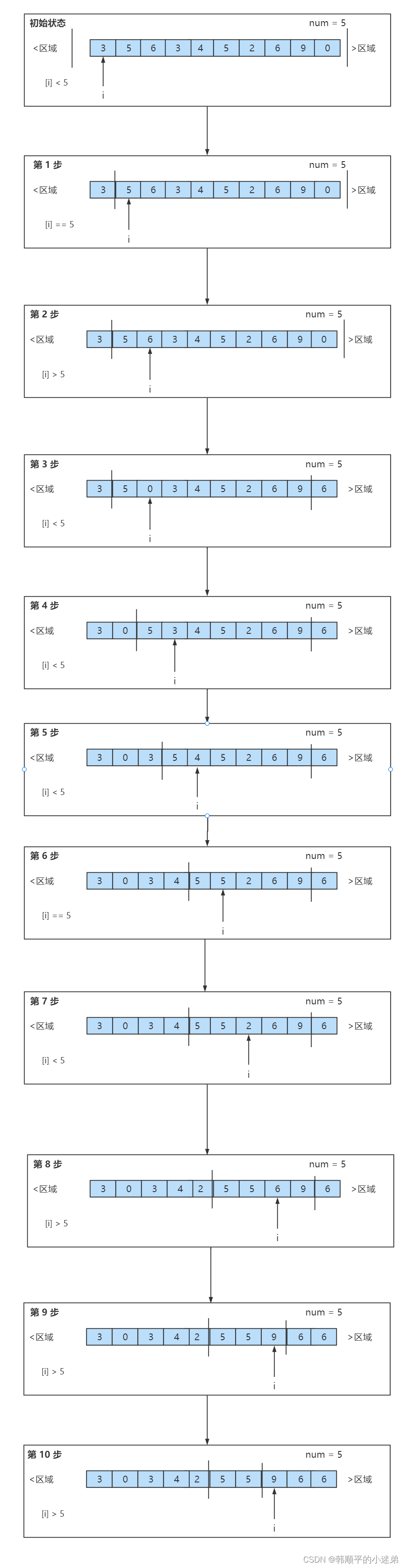
给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的 右边。要求额外空间复杂度O(1)，时间复杂度O(N)
解决方案:
划定一个<区域 ，初始化为-1，一个>区域，初始化为arr.length()，一个指针i 初始化指向arr[0],arr[i]与num比较大小:

  1. arr[i] < num; arr[i] 和 <区域的下一个数交换， <区域右扩一个，同时 i++;
    2)arr[i] == num; i++
  2. arr[i] > num; arr[i] 和 >区域的前一个数交换，>区域左扩一个;

例子:arr = [3,5,6,3,4,5,2,6,9,0], num = 5。整个流程如下:
在这里插入图片描述
java代码:

//在数组arr中，把小于num的数放在数组左边，等于num的数放在中间，大于num的数放在右边
    public static int[] version2(int[] arr, int left, int right) {
        int leftArea = left -1;
        int rightArea = right + 1;
        int i = left;
        int num = arr[right];
        while (i != rightArea) {
            if (arr[i] < num) {
                swap(arr, i++, ++leftArea);
            }
            else if (arr[i] == num) {
                i++;
            }
            else {
                swap(arr, i, --rightArea);
            }
        }
        System.out.println("leftArea:" + leftArea + "\trightArea:" + rightArea);
        int[] res = {leftArea, rightArea};
        return res;
    }

随机快速排序（改进的快速排序）:

1）在数组范围中，等概率随机选一个数作为划分值，然后把数组通过荷兰国旗问题分成三个部分：左侧<划分值、中间==划分值、右侧>划分值
2）对左侧范围和右侧范围，递归执行
3）时间复杂度为O(N*logN)

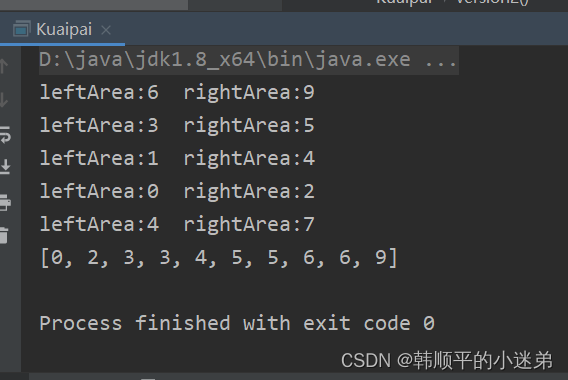
快排代码如下:

package paixu;

import java.util.Arrays;

public class Kuaipai {
    public static void main(String[] args) {
        int[] arr = {3,5,6,3,4,5,2,6,9,0};
        kuaipai(arr, 0,9);
        System.out.println(Arrays.toString(arr));
    }

    //在数组arr中，把小于num的数放在数组左边，等于num的数放在中间，大于num的数放在右边
    public static int[] version2(int[] arr, int left, int right) {
        int leftArea = left -1;
        int rightArea = right + 1;
        int i = left;
        int num = arr[right];
        while (i != rightArea) {
            if (arr[i] < num) {
                swap(arr, i++, ++leftArea);
            }
            else if (arr[i] == num) {
                i++;
            }
            else {
                swap(arr, i, --rightArea);
            }
        }
        System.out.println("leftArea:" + leftArea + "\trightArea:" + rightArea);
        int[] res = {leftArea, rightArea};
        return res;
    }

    public static void kuaipai(int[] arr, int L, int R) {
        if (L < R) {
            swap(arr, L + (int)(Math.random() * (R - L - 1)), R);
            int[] p = version2(arr, L, R);
            kuaipai(arr, L, p[0]);
            kuaipai(arr, p[1], R);
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

结果如下:
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/162405.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

浅谈非类型模板参数、模板的特化

浅谈非类型模板参数、模板的特化

非类型模板参数 1.模板参数分类类型形参与非类型形参。 2.类型形参即&#xff1a;出现在模板参数列表中&#xff0c;跟在class或者typename之类的参数类型名称。类型参数也可以给缺省值 3.非类型形参&#xff0c;就是用一个常量作为类(函数)模板的一个参数&#xff0c;在类(函…
阅读更多...
FARO RevEng Software 22.3.9 Crack

FARO RevEng Software 22.3.9 Crack

FARO RevEng Software 22.3.9 用于反向工程的三维点云捕捉和网格生成 先进的 FARO RevEng 软件平台能为用户带来全面的数字设计体验。该反向工程软件有助于利用三维点云创建和编辑高质量的网格和 CAD 表面&#xff0c;以实现反向工程工作流程。然后&#xff0c;工业设计师可以利…
阅读更多...
Zookeeper 集群安装

Zookeeper 集群安装

Zookeeper 集群 主机 IP SoftWare Port OS Myidnode1 192.168.230.128 apache-zookeeper-3.7.1 2181 Centos 7 1 node2 192.168.230.129 apache-zookeeper-3.7.1 2181 Centos 7 2 node3 192.168.230.130 apache-zookeeper-3.7.1 2181 Centos 7 31. 下载 Apache Downloads 下…
阅读更多...
2022简单一年

2022简单一年

牙齿软件决定开发的时间是2021年底&#xff0c; 老板说2022年任务是要开发牙齿咬合力的软件&#xff0c; 功能主要借鉴美国的一款软件,老板给了我一份软件的说明书&#xff0c; 包含了软件的所有功能。 看到软件第一感觉是&#xff0c; 做的确实是牛逼&#xff0c; 并且各…
阅读更多...
【十 二】Netty 文件传输

【十 二】Netty 文件传输

概念介绍 文件是最常见的数据源之一&#xff0c;程序经常需要在文件中读取数据&#xff0c;也要将数据保存在文件中&#xff0c;进行持久化。 文件是计算机中一种基本的数据存储形式。即使计算机关机&#xff0c;文件的数据还是存在的&#xff0c;但是内存的数据就会丢失。 相…
阅读更多...
联合证券|五定增项目同日被否 保荐机构该不该“背锅”？

联合证券|五定增项目同日被否 保荐机构该不该“背锅”？

一天之内5家上市公司定增一起被拒&#xff0c;这一音讯瞬间引发商场重视。 1月11日&#xff0c;浙江世宝、铭普光磁、胜华新材、日辰股份、振华科技等5家上市公司一起公告称&#xff0c;定增不被证监会受理&#xff0c;理由均是证监会以为请求资料不符合法定方式。 投行业界人…
阅读更多...
18.Isaac教程--坐标系

18.Isaac教程--坐标系

坐标系 本节介绍相机、网格/矩阵/图像和机器人坐标系。 ISAAC教程合集地址: https://blog.csdn.net/kunhe0512/category_12163211.html 文章目录坐标系网格像素中心网格/矩阵/图像坐标系相机坐标系机器人坐标系网格像素中心 存储网格 GGG 上的值&#xff0c;使得网格单元将值…
阅读更多...
Crack：CAD Exchanger GUI/CAD Exchanger Lab 不是SDK

Crack：CAD Exchanger GUI/CAD Exchanger Lab 不是SDK

CAD Exchanger GUI/CAD Exchanger Lab 用于查看、转换和分析 CAD、BIM 和 3D 数据 在 Windows、Mac 和 Linux 上加载和转换模型&#xff0c;而无需处理昂贵的 CAD 系统。 使用 CATIA、SOLIDWORKS、Creo、STEP、JT、IFC 和更多格式。 非常适合您的 3D 数据工作流程 连接不同的软…
阅读更多...
多频电磁仪在2018年杭州电磁大会的报告（ICEEG）

多频电磁仪在2018年杭州电磁大会的报告（ICEEG）

本篇是对多频电磁方法，应用的解读。 本汇报讲述了EMI传感器的基本情况，以及用手持多频电磁仪进行实际探测应用的例子。 什么是电磁感应？用发射装置（TX）激发谐波，产生一次场（Primary field），地下导体目标会相应产生涡流电磁场，产生二次场，被接收装置（RX）探测到。 …
阅读更多...
超参数、划分数据集、偏差与方差、正则化

超参数、划分数据集、偏差与方差、正则化

目录1.超参数(hyperparameters)参数(Parameters)&#xff1a;&#xff0c;&#xff0c;&#xff0c;&#xff0c;&#xff0c;...超参数&#xff1a;能够控制参数W,b的参数&#xff0c;是在开始学习之前设置的参数。比如&#xff1a;学习率、梯度下降循环的数量#iterations、隐…
阅读更多...
力扣sql基础篇(七)

力扣sql基础篇(七)

力扣sql基础篇(七) 1 统计各专业学生人数 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 想要没有学生的部门也保存,就得以部门表作为主表 #字母表顺序就是升序 SELECT d.dept_name,IFNULL(s1.number,0) student_number FROM Department d LEFT …
阅读更多...
2022. 12 青少年机器人技术等级考试理论综合试卷（二级）

2022. 12 青少年机器人技术等级考试理论综合试卷（二级）

2022.年12月青少年机器人技术等级考试理论综合试卷&#xff08;二级&#xff09; 一、 单选题(共 30 题&#xff0c; 共 60 分) 1.“机器人三原则” 是由谁提出的&#xff1f; &#xff08; &#xff09; A.美国人艾萨克 阿西莫夫 B.日本人森昌弘 C.美国人乔治 德沃尔 D.中国人…
阅读更多...
谈谈 MongoDB 中连接池、索引、事务等问题

谈谈 MongoDB 中连接池、索引、事务等问题

大家好&#xff0c;三分钟你将学会&#xff1a; MongoDB连接池的使用方式与常用参数查询五步走&#xff0c;能活九十九&#xff1f;MongoDB索引与MySQL索引有何异同&#xff1f;MongoDB事务与ACID什么是聚合框架&#xff1f;在最开始接触MongoDB的时候&#xff0c;是通过 Mong…
阅读更多...
H3C V7MSR路由器定时限速的典型应用配置

H3C V7MSR路由器定时限速的典型应用配置

某公司希望在上班时间对员工进行每IP限速&#xff0c;其他时间不限制。 1.主要配置如下&#xff1a; #创建关闭接口g0/1的限速功能 scheduler job close-car-g0/1 command 1 system-view command 2 interface g0/1 command 3 undo qos car inbound carl 1 #创建开启接口g0…
阅读更多...
什么是CISP-ICSSE？到底该不该考？

什么是CISP-ICSSE？到底该不该考？

CISP-ICSSE注册信息安全专业人员-工业控制系统安全工程师&#xff0c;英文为 Certified Information Security Professional-ICS Security Engineer&#xff0c;简称 CISP-ICSSE。 持证人员可以从事信息安全技术领域工业控制系统安全方向的工作&#xff0c;具备制定工 控安全威…
阅读更多...
74. 序列模型

74. 序列模型

1. 序列数据 实际中很多数据是有时序结构的例如&#xff0c;电影的评价随时间变化而变化 拿奖后评分上升&#xff0c;直到奖项被忘记看了很多好电影后&#xff0c;人们的期望变高季节性&#xff1a;贺岁片、暑期档导演、演员的负面报道导致评分变低 2. 序列数据-更多例子 音…
阅读更多...
【文件操作】C语言

【文件操作】C语言

目录1. 为什么使用文件2. 什么是文件2.1 程序文件2.2 数据文件2.3 文件名3. 文件的打开和关闭3.1 文件指针3.2 文件的打开和关闭4. 文件的顺序读写5. 文件的随机读写5.1 fseek5.2 ftell5.3 rewind6. 文本文件和二进制文件7. 文件读取结束的判定8. 文件缓冲区1. 为什么使用文件 …
阅读更多...
NodeMCU esp8266的网络连入网络的模式方式即程序实例

NodeMCU esp8266的网络连入网络的模式方式即程序实例

接入WIFI模式 参考&#xff1a;http://www.taichi-maker.com/homepage/esp8266-nodemcu-iot/internet-basics/link-layer/ 模式1 – 无线终端模式&#xff08;Wireless Station&#xff09; 简单说就是把这个开发板做为终端连入WiFi 程序实例 需要注意&#xff1a;端口号…
阅读更多...
TikTok的崛起历程：我们所有人都看到了这种潜力

TikTok的崛起历程：我们所有人都看到了这种潜力

武汉瑞卡迪电子商务有限公司&#xff1a;在短短五年里&#xff0c;TikTok已经爆发成为一种流行文化现象以及一个地缘政治闪爆点。它是全世界最热门的应用&#xff0c;被2/3的美国青少年所使用。它的超级吸引人的短视频格式已经让硅谷争相效仿&#xff0c;并使一夜成名变得比以前…
阅读更多...
Linux常用命令——vi命令

Linux常用命令——vi命令

在线Linux命令查询工具(http://www.lzltool.com/LinuxCommand) vi 功能强大的纯文本编辑器 补充说明 vi命令是UNIX操作系统和类UNIX操作系统中最通用的全屏幕纯文本编辑器。Linux中的vi编辑器叫vim&#xff0c;它是vi的增强版&#xff08;vi Improved&#xff09;&#xff…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023