题目描述

五子棋是世界智力运动会竞技项目之一，是一种两人对弈的纯策略型棋类游戏，通常双方分别使用黑白两色的棋子，下在棋盘直线与横线的交叉点上，先形成连续的五子连线（横、竖、斜）者获胜。

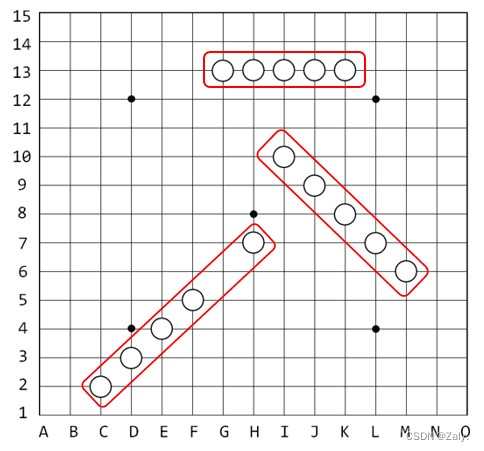
棋盘一般为15X15的，横向为A～O，纵向为1～15，从棋盘的左下角开始标记，如下图所示。例如，图示中上面的5个棋子可标记为G13、H13、I13、J13、K13，正好形成横向五子连线的情况；图示中右方的5个棋子可标记为I10、J9、K8、L7、M6，正好形成斜向五子连线的情况；图示中左下方的5个棋子可标记为H7、F5、E4、D3、C2，未能形成五子连线的情况。

现给出5个棋子的位置，请判断这5个棋子有没有形成五子连线的情况?

输入

第一行输入一个整数n（1≤n≤200），代表有n组测试数据。

接下来有n行数据，每行一组数据，每组数据包括5个棋子的位置。

输出

如果5个棋子可以形成五子连线的情况（横向、竖向、斜向），输出Yes，否则输出No。

每个输出占一行。

样例输入

3
G13 K13 J13 I13 H13
I10 J9 M6 L7 K8
H7 E4 F5 D3 C2

样例输出

Yes
Yes
No

算法思路

输入

考虑到有多组复杂的数据，所以选择采用结构体的数据结构。读取的时候我们将横坐标（字母）和纵坐标（数字）分别读取并存放到结构体下的两个数组alp和dig中。

五子连线的判定

拿到了坐标，判定是否连成五子只需要分三大类讨论

• 字母连续的情况
• 字母相等的情况
• 其他情况

在字母连续的情况下需要分两小类

• 数字相等 或 数字字母（横纵坐标）差相等 或 数字字母（横纵坐标）和相等
• 其他情况

在字母相等的情况下也需要分两小类 

• 数字连续
• 数字不连续

坐标连续的判定

按照上述思路我们在讨论的时候要对数字和字母的连续性进行判定，这时候采用排序是很好的办法，通过<stdlib.h>中的qsort函数可以帮助我们省掉一些麻烦。因为只有5个坐标，采用硬核一点的办法直接判定五个是不是连续就行了。

小心坑

• 输入的时候每读完一个坐标要用一个getchar()清空缓冲区，否则会得到不期望的结果
• 要先计算横纵坐标差再给数组排序，因为排序之后横纵坐标就不再在同一索引对应

代码

以上只是我个人的思路，并不代表着最优解，代码仅供参考。

#include <stdio.h>
#include <stdlib.h>
struct chess{
    char alp[5];
    int dig[5];
};
int as_int(const void* e1, const void* e2) {
    return *(int*)e1 - *(int*)e2;
}
int as_char(const void* e1, const void* e2) {
    return (*(char*)e1) - (*(char*)e2);
}
int main(){
    int n;
    scanf("%d",&n);
    getchar();
    struct chess groups[n];
    for(int i=0;i<n;i++){
        for(int j=0;j<5;j++){
            scanf("%c%d",&groups[i].alp[j],&groups[i].dig[j]);
            getchar();
        }
    }
    for(int i=0;i<n;i++){
        int a1,a2,a3,a4,a5,d1,d2,d3,d4,d5;
        a1=groups[i].dig[0]+groups[i].alp[0];
        a2=groups[i].dig[1]+groups[i].alp[1];
        a3=groups[i].dig[2]+groups[i].alp[2];
        a4=groups[i].dig[3]+groups[i].alp[3];
        a5=groups[i].dig[4]+groups[i].alp[4];
        d1=groups[i].dig[0]-groups[i].alp[0];
        d2=groups[i].dig[1]-groups[i].alp[1];
        d3=groups[i].dig[2]-groups[i].alp[2];
        d4=groups[i].dig[3]-groups[i].alp[3];
        d5=groups[i].dig[4]-groups[i].alp[4];
        qsort(groups[i].dig, 5, sizeof(int), as_int);
        qsort(groups[i].alp, 5, sizeof(char), as_char);
        if(groups[i].alp[0]+1==groups[i].alp[1]&&groups[i].alp[1]+1==groups[i].alp[2]&&groups[i].alp[2]+1==groups[i].alp[3]&&groups[i].alp[3]+1==groups[i].alp[4]){
            if((groups[i].dig[0]==groups[i].dig[1]&&groups[i].dig[0]==groups[i].dig[2]&&groups[i].dig[0]==groups[i].dig[3]&&groups[i].dig[0]==groups[i].dig[4])||(a1==a2&&a2==a3&&a3==a4&&a4==a5)||(d1==d2&&d2==d3&&d3==d4&&d4==d5)){
                printf("Yes\n");
            }
            else{
                printf("No\n");
            }
        }
        else if(groups[i].alp[0]==groups[i].alp[1]&&groups[i].alp[0]==groups[i].alp[2]&&groups[i].alp[0]==groups[i].alp[3]&&groups[i].alp[0]==groups[i].alp[4]){
            if(groups[i].dig[0]+1==groups[i].dig[1]&&groups[i].dig[1]+1==groups[i].dig[2]&&groups[i].dig[2]+1==groups[i].dig[3]&&groups[i].dig[3]+1==groups[i].dig[4]){
                printf("Yes\n");
            }            
            else{
            printf("No\n");
            }
        }
        else{
            printf("No\n");
        }
    }
    return 0;
}