目录
一、斐波那契数列的基本概念
二、动态规划在斐波那契数列中的应用与优势
三、实际案例:使用动态规划解决斐波那契数列问题
四、动态规划问题的做题步骤
五、例题
1、第N个泰波那契数---点击跳转题目
2、三步问题----点击跳转题目
3、最小花费爬楼梯----点击跳转题目
4、解码方法----点击跳转题目
本文通过对斐波那契数列问题引入动态规划,这也是动态规划问题中比较简单的一类问题,通过这个模型我们一起来学习什么是动态规划算法并且动态规划问题的基本做题步骤是什么
一、斐波那契数列的基本概念
斐波那契数列是这样一个数列:从第三项开始,每一项都等于前两项之和。数列的前几项为:0, 1, 1, 2, 3, 5, 8, 13, 21, ...。这个数列的特性使得它在很多实际问题中都有着重要的应用。
二、动态规划在斐波那契数列中的应用与优势
在计算斐波那契数列时,我们可以使用递归的方式。然而,递归方式在计算较大的斐波那契数时,会存在大量的重复计算,效率非常低。而动态规划技术可以有效地避免这种重复计算,显著提高计算效率。
动态规划的基本思想是将问题分解为若干个子问题,并将这些子问题的解保存起来,以便在计算新的子问题时能够直接利用之前的结果,避免重复计算。在斐波那契数列问题中,我们可以使用动态规划技术,从下往上计算斐波那契数列,并将每个计算结果保存起来,这样在计算较大的斐波那契数时,就可以直接使用之前保存的结果,通过空间换时间的操作,大大提高了计算效率。
三、实际案例:使用动态规划解决斐波那契数列问题
下面是一个C++代码示例,展示了如何使用动态规划来计算斐波那契数列:
#include<iostream>
const int N = 100;
int dp[N];
int main()
{
dp[0] = 1,dp[1] = 1;
int n;cin>>n;
for(int i=2;i<=n;i++)
dp[i] = dp[i-1] + dp[i-1];
cout<<dp[n]<<endl;
return 0;
}在上述代码中,我们创建了一个列表dp来保存斐波那契数列的值。初始时,列表的前两个元素被设置为斐波那契数列的前两项。然后,我们通过一个循环,从第三项开始,依次计算斐波那契数列的每一项,并将结果保存在dp列表中。最后,返回dp[n],即第n项斐波那契数的值。
动态规划在斐波那契数列中的核心思想是通过保存子问题的解来避免重复计算。具体方法是将问题分解为子问题,并按照某种顺序(如上述示例中的从下往上)依次解决这些子问题,同时保存每个子问题的解。在计算新的子问题时,如果其解已经保存,则直接利用保存的解,否则通过解决更小的子问题来得到其解,并将解保存起来。
四、动态规划问题的做题步骤
在分析题目时分为五步:
- 状态表示:根据 经验 + 题目要求 得出
dp[i]代表什么? 一般可以 以i为结尾 或 以i为起点 做状态表示
- 状态转移方程:根据dp[i]的最近一步推导得出关于dp[i]的递推公式
- 初始化:根据递推公式来初始化需要先用到的dp值
- 填表顺序:根据递推公式来判断填表顺序
- 返回值:题目要求
在编写代码时分为四步:
- 创建dp表
- 初始化
- 填表
- 返回值
五、例题
1、第N个泰波那契数---点击跳转题目

本题很简单明了,题目里面就已经给出了状态转移方程,由此,我们定义dp[n]是第n个泰波斐契数
代码:
class Solution {
public:
int m = 40;
int tribonacci(int n)
{
//空间优化
if(n == 0) return 0;
if(n == 1 || n == 2) return 1;
int a = 0,b = 1, c = 1,d;
for(int i=3;i<=n;i++)
{
d = a + b + c;
//滚动操作
a = b; b = c; c = d;
}
return d;
}
};由于每个数只会用到它的前三个数,所以我们可以使用滚动数组来进行空间优化
2、三步问题----点击跳转题目

分析:
- 状态表示:以i为结尾分析,dp[i]为到第i个台阶的方法总数
- 状态转移方程:分析最近一步,由于一次可以跨1到3个台阶,所以到第i个台阶的最近一步就是先到i-1、i-2、i-3这三个台阶,再分别跨1、2、3个台阶到达第i个台阶,那么从i-1层到i层这种方式到i层的方法数就是到i-1层的方法数,以此类推:dp[i] = dp[i-1]+dp[i-2]+dp[i-3]; 可以看出递推公式和上一题一摸一样,只不过这个需要我们根据题意和经验自己推导。
- 初始化:把上1、2、3层的台阶方法数先初始化,因为递推公式要用到三个数,根据题意,dp[1] = 1,dp[2] = 2,dp[3] = 4;
- 填表顺序:由于递推公式是由小推大,所以从左向右填表
- 返回值:根据题意,返回dp[n] 对1000000007取模的结果即可
代码:
class Solution {
public:
int waysToStep(int n)
{
int MOD = 1e9 + 7;
//创建dp表
vector<int> dp(10+n);
//初始化
dp[1] = 1;dp[2] = 2;dp[3] = 4;
//填表
for(int i=4;i<=n;i++)
dp[i] = ((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;
//返回值
return dp[n];
}
};题意是结果取模即可,但是因为数值过大,计算过程中就会爆数据范围,所以只能每做一次加法取一次模,和对结果取模等价; 注意,取模运算具有分配律:(A+B)%C = A%C + B%C
3、最小花费爬楼梯----点击跳转题目

分析:题中表示,从第i层向上爬,需要花费cost[i]的体力值,可以从0、1层向上爬,也就死选择到0/1层并不花费体力值;
- 状态表示:以i为结尾,dp[i]:到第i层花费的最小体力值
- 状态转移方程:由dp[i]最近一步推导,由于一次可以爬1~2步,到第i层之前,要么在i-1层,要么在i-2层,分类讨论,从i-1层到i层的最小花费为:dp[i-1]+cost[i-1];从i-2层到i层的最小花费为:dp[i-2]+cost[i-2],一共这两种情况,哪一种才是到达i层的最小花费呢?两者取个最小值即可:dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
- 初始化:由递推公式可知需要前两个dp值,由题意,选择上0或1层台阶不花费体力值,dp[0] = dp[1] = 0
- 填表顺序:由递推公式是在小推大,所以我们从左向右填表
- 返回值:根据题意,返回dp[n]就是到达第n层台阶的最小花费
代码:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
vector<int> dp(10+n);
dp[0] = dp[1] = 0;
for(int i=2;i<=n;i++)
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
return dp[n];
}
};看到这里,可能有读者会有疑惑,分析状态表示时这三个题怎么都是以i为结尾分析,做题步骤中不是还有以i为起点分析吗?其实都可以,做题的时候觉得怎样更方便就选择怎样,那么这道题我们也以i为起点来举例分析一下
- 状态表示:以i为起点,dp[i]表示以i为起点到楼顶的最小花费
- 状态转移方程:分析dp[i]最近的一步,以i为起点,自然只能向后看,最近的一步就是i+1层台阶和i+2层台阶; dp[i] = cost[i] + min(dp[i+1],dp[i+2])
- 初始化:由递推公式可知,是要先直到后面的值推导前面的值,dp[n] = 0, dp[n-1] = cost[i-1]
- 填表顺序:由递推公式,是大推小,所以是从右往左填表
- 返回值:根据题意,要求的是从0层或1层到n层的最小花费,所以结果为min(dp[0],dp[1])
代码:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost)
{
//dp[i]:以i位置出发到达楼顶的最小花费
//dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
int n = cost.size();
vector<int> dp(n+10);
dp[n] = 0;dp[n-1] = cost[n-1];
for(int i=n-2;i>=0;i--)
dp[i] = cost[i] + min(dp[i+1],dp[i+2]);
return min(dp[0],dp[1]);
}
};这道题怎么分析都可以,建议两种视角都看一遍加深理解
4、解码方法----点击跳转题目

分析:一个字符要么单独解码,要么合并另一个字符解码,合并时前导0情况表示解码失败
- 状态表示:以i为结尾,dp[i]表示以i为结尾时的解码方法总数
- 状态转移方程:根据dp[i]最近的一步,就是以i位置的字符单独解码或者i和i-1的字符合并解码两种情况,其中每种情况都要判断其合法性,是否能解码成功,解码失败则表示i位置这种情况下的解码方法数是0,如果两种情况都解码成功,dp[i] = dp[i-1] + dp[i-2]
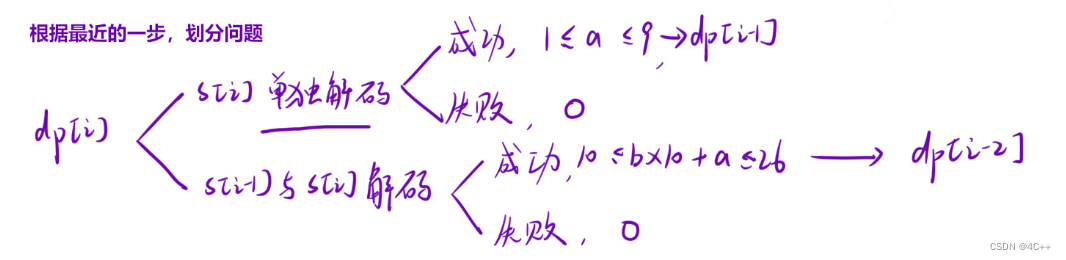
- 初始化:初始化0,1即可,根据是否能解码成功来分类
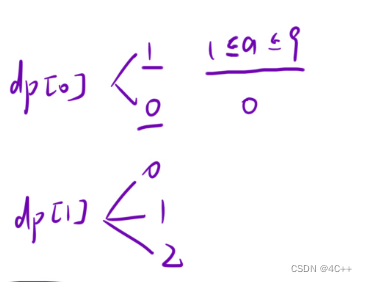
- 填表顺序:从左往右
- 返回值:dp[s.size()]
代码:
class Solution {
public:
int numDecodings(string s)
{
int n = s.size();
vector<int> dp(10+n);
if(s[0]-'0' != 0) dp[0] = 1;
else dp[0] = 0;
if(s[0]-'0' && s[1]-'0') dp[1]++;
int t = (s[0]-'0')*10 + s[1] - '0';
if(t>=10 && t<= 26) dp[1]++;
for(int i=2;i<n;i++)
{
if(s[i] != '0') dp[i] += dp[i-1];
int t = (s[i-1] - '0')*10 + s[i] - '0';
if(10<=t && t<=26) dp[i] += dp[i-2];
}
return dp[n-1];
}
};