【一刷剑指Offer】面试题 8：旋转数组的最小数字

news2024/11/16 6:04:58

力扣对应题目链接：154. 寻找旋转排序数组中的最小值 II - 力扣（LeetCode）

牛客对应题目链接：旋转数组的最小数字_牛客题霸_牛客网 (nowcoder.com)

核心考点 ：数组理解，二分查找，临界条件。

一、《剑指Offer》对应内容

二、分析题目

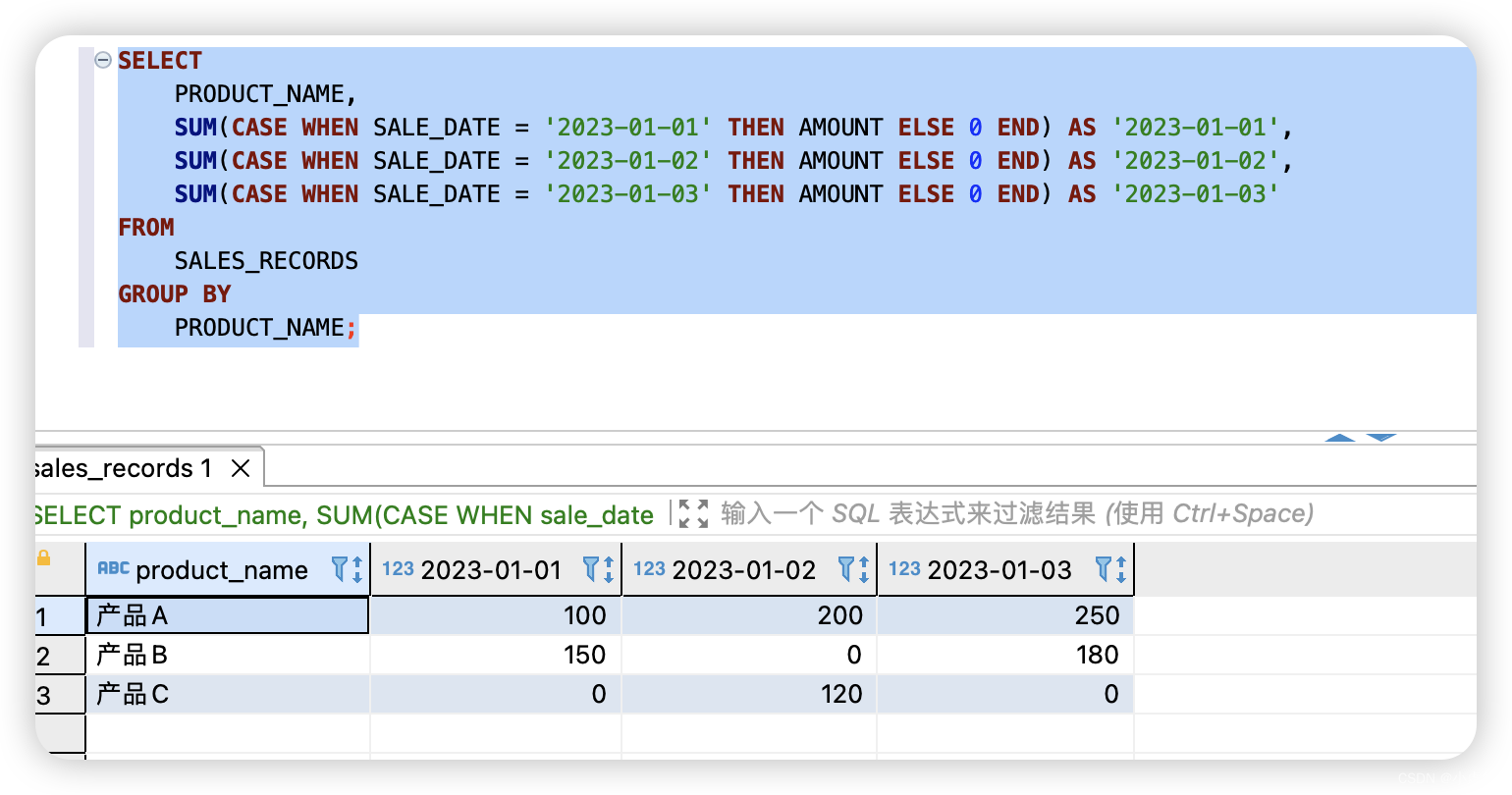
数组问题的本质：求最小值问题。

1、方法一

理论上遍历一次即可，但是我们可以根据题意选择使用稍微高效且更简单一点的做法。
按照题目要求，要么是一个非递减排序的数组（最小值在最开始），要么是一个旋转（最小值在中间某个地方）。
在旋转之后有个特征：在遍历的时候原始数组是非递减的，在旋转之后就有可能出现递减，引起递减的数字就是最小值。

2、方法二

采用二分查找的方式，进行定位。二分的本质是二段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用二分。
定义首尾下标，因为是非递减数组旋转，所以旋转后可以将数组看成两部分，前半部分整体非递减，后半部分整体非递减，前半部分整体大于后半部分。
所以，我们可以假设如下定义，让 left 指向最左侧，right 指向最右侧，mid 为二分之后的中间位置。我们假设 nums[nums.size()-1]（或 num[0]）为 x，如果 nums[mid] > nums[x] 时，说明 mid 位置在原数组前半部分，也就是说，目标最小值在 mid 的右侧，那么我们让 left=mid+1。否则，说明 mid 位置在原数组后半部分，也就是说，目标最小值在 mid 的右侧，让那么我们让 right=mid。
上述这个过程，会让 [left, right] 这个区间缩小。在这个过程中，left 永远在原数组前半部分，right 永远在原数组的后半部分，而范围会一直缩小。当不满足 left < right 时，left 指向的位置就是最小元素的位置。
但是因为题目说的是非递减，也就意味着数据允许重复，因为有重复数据的可能，这意味着我们无法直接根据与 nums[0] 或 nums[nums.size()-1] 的大小关系，将数组划分为两段，即无法通过二分来找到旋转点。
这时，我们就需要判断重复元素是否存在于两端，通过移动指针来避免数据重复的影响。

三、代码（C++）

本题是153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）的延伸，可以先尝试第 153 题（区别：153 题元素值互不相同，没有重复值），体会在旋转数组中进行二分查找的思路，再来尝试解决本题。

因为这里找到的题目链接的数据范围都是数组长度 >= 1 的，所以这里就不做判空处理了。

这里贴出 AC 代码：（可以看看两体之间的区别）

//推荐：二分-取右端点为比较值 O(logN)
class Solution {
public:
    int findMin(vector<int>& nums) {
        int n=nums.size();
        int left=0, right=n-1;
        int x=nums[n-1];
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>x) left=mid+1;
            else right=mid;
        }
        return nums[left];
    }
};

//不推荐：二分-取左端点为比较值 O(logN)
class Solution {
public:
    int findMin(vector<int>& nums) {
        int n=nums.size();
        if (n==1 || nums[0]<nums[n-1]) return nums[0];
        int left=0, right=n-1;
        int x=nums[0];
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>=x) left=mid+1;
            else right=mid;
        }
        return nums[left];
    }
};

1、方法一（题目要求尽可能减少整个过程的操作步骤，所以推荐写方法二）

//暴力解法一
class Solution {
public:
    int findMin(vector<int>& nums) {
        int n=nums.size();
        int res=INT_MAX;
        for(int i=0; i<n; i++)
            if(res>nums[i])
                res=nums[i];
        return res;
    }
};

//暴力解法二（上述描述写法）
class Solution {
public:
    int findMin(vector<int>& nums) {
        int res=nums[0];
        int n=nums.size();
        for(int i=1; i<n; i++)
        {
            if(nums[i-1]>nums[i])
            {
                res=nums[i];
                break;
            }
        }
        return res;
    }
};

2、方法二

//推荐：二分-取右端点为比较值 O(logN)
class Solution {
public:
    int findMin(vector<int>& nums) {
        int n=nums.size();
        int left=0, right=n-1;
        while(left<right && nums[0]==nums[right])
            right--;
        int x=nums[right];
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>x) left=mid+1;
            else right=mid;
        }
        return nums[left];
    }
};

//牛客网
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型vector 
     * @return int整型
     */
    int minNumberInRotateArray(vector<int>& nums) {
        int n=nums.size();
        int left=0, right=n-1;
        while(left<right && nums[0]==nums[right])
            right--;
        int x=nums[right];
        while(left<right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>x) left=mid+1;
            else right=mid;
        }
        return nums[left];
    }
};