在之前文章 分类分析|贝叶斯分类器及其Python实现中，我们对分类分析和分类模型进行了介绍，这里

1. KNN算法思想

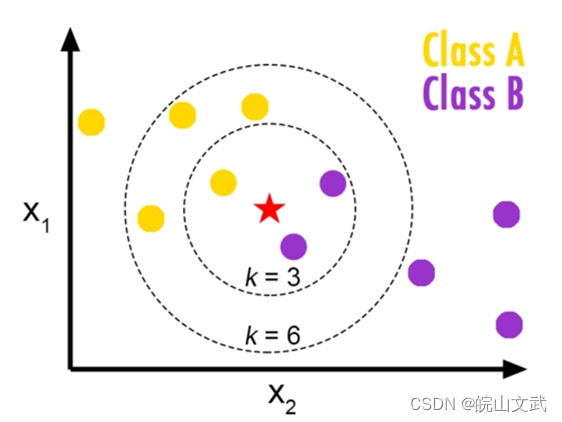
 KNN（K-Nearest Neighbor）最邻近分类算法是一种基于类比学习的分类算法，其指导思想是”近朱者赤，近墨者黑“，即由你的邻居来推断出你的类别。其算法原理是在训练数据集中找出K个与预测样本距离最近且最相似的样本，这些样本大部分属于哪个类别，则该预测样本也属于哪个类别。
 KNN分类算法的实现原理：为了判断未知样本的类别，以所有已知类别的样本作为参照，计算未知样本与所有已知样本的距离，从中选取与未知样本距离最近的K个已知样本，根据少数服从多数的投票法则（majority-voting），将未知样本与$K$个最邻近样本中所属类别占比较多的归为一类。

 $k$最近邻分类主要的问题是确定样本集、距离函数、组合函数和$k$值。

2. KNN算法步骤

1. 计算预测数据样本与各个训练数据样本之间的距离；
2. 按照距离的递增关系进行排序；
3. 选取距离最小的K个数据样本（前面K个）；
4. 确定前K个数据样本所在类别的出现频率；
5. 前K个数据样本中出现频率最高的类别作为预测数据样本的类别。

2.1 KNN主要优点

(1) 简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归。
(2) 可用于数值型数据和离散型数据。
(3) 训练时间复杂度为$O(n)$，无数据输入假定。
(4) 对异常值不敏感。

2.2 KNN主要缺点

KNN算法是目前较为常用且成熟的分类算法，但是KNN算法也有一定的不足:
(1) 计算复杂性高、空间复杂性高。
(2) 当样本不平衡（有些类别的样本数量很大，而其它样本的数量又很少）时，容易产生误分。
(3) 一般样本数量很大的时候不用KNN，因为计算量很大。但是数据样本量又不能太少，此时容易产生误分。
(4) 无法给出数据的内在含义。

3. Python实现KNN分类算法

3.1 自定义方法实现KNN分类

 下例中，假设训练集数据为学生各门课程测验成绩，标签为综合等级评价。利用KNN方法对样本进行分类预测。

#trainData-训练集、testData-测试集、labels-分类
def knn(trainData, testData, labels, k):
    rowSize = trainData.shape[0] #计算训练样本的行数
    diff=np.tile(testData,(rowSize,1))-trainData #计算训练样本和测试样本的差值
    sqrDiff = diff ** 2  #计算差值的平方和
    sqrDiffSum = sqrDiff.sum(axis=1)
    distances = sqrDiffSum ** 0.5  #计算距离
    sortDistance = distances.argsort() #对所得的距离从低到高进行排序
    count = {}
    for i in range(k):
        vote = labels[sortDistance[i]]
        count[vote] = count.get(vote, 0) + 1
        sortCount = sorted(count.items(),reverse=True) #对类别出现的频数从高到低进行排序
    return sortCount[0][0] #返回出现频数最高的类别
import numpy as np
trainData = np.array([[100,100,100],[90,98,97],[90,90,85],
[100,90,93],[80,90,70],[100,80,100],[95,95,95],[95,90,80],
[90,75,90],[95,95,90],[100,100,95]])
labels = ['优', '良', '中', '良','中','良','优','中','中','良','优']
testData = [97,96,92]
X = knn(trainData, testData, labels, 3)
print(X)

输出结果：良

3.2 调用scikit-learn模块实现KNN分类

 在scikit-learn 中，与KNN法这一大类相关的类库都在sklearn.neighbors包之中。当使用函数KNeighborsClassifier()进行分类时，需要导入相关的类库，语句为：from sklearn import neighbors。常用形式为：
KNeighborsClassifier(n_neighbors=5,weights=’uniform’)

KNeighborsClassifier函数一共有8个参数，参数说明：

1. n_neighbors：KNN中的k值，int，默认为5。
2. weights： 默认是uniform，参数可以是uniform、distance，也可以是用户自己定义的函数（直接weights=函数名就行）。uniform是均等的权重，就说所有的邻近点的权重都是相等的。distance是不均等的权重，距离近的点比距离远的点的影响大。用户自定义的函数，接收距离的数组，返回一组维数相同的权重。
3. algorithm： {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’。快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
4. leaf_size： int ，default=30。leaf_size：默认是30，这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度，同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
5. metric： str or callable, default=’minkowski’。用于距离度量，默认度量是minkowski（也就是闵氏距离，当p=2时为欧氏距离(欧几里德度量)。
6. p： 距离度量公式。即设置metric里闵氏距离的参数p，这个参数默认为2，也就是默认使用欧式距离公式进行距离度量。也可以设置为1，使用曼哈顿距离公式进行距离度量。
7. metric_params： 距离公式的其他关键参数，这个基本不用，使用默认的None即可。
8. n_jobs：并行处理设置。默认为1，临近点搜索并行的工作数。如果为-1，那么CPU的所有cores都用于并行工作。

例： 对鸢尾花数据集进行分类

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 11 #取k=11
iris = datasets.load_iris()  #导入鸢尾花数据集
x = iris.data[:,:2]  #取前两个feature,方便在二维平面上画图
y = iris.target
h = .02  #网格中的步长
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])# 创建彩色的图
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
for weights in ['uniform', 'distance']: #绘制两种weights参数的KNN效果图  
    clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)  # 创建了一个KNN分类器的实例，并拟合数据
    clf.fit(x, y)
    # 绘制决策边界。为此，将为每个数据对分配一个颜色来绘制网格中的点 [x_min, x_max]、[y_min, y_max]
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    # 将结果放入一个彩色图中
    Z = Z.reshape(xx.shape)
    plt.figure()
    plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
    # 绘制训练点
    plt.scatter(x[:, 0], x[:, 1], c=y, cmap=cmap_bold)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.title("3-Class classification (k = %i, weights = '%s')"
             % (n_neighbors, weights))
plt.show()

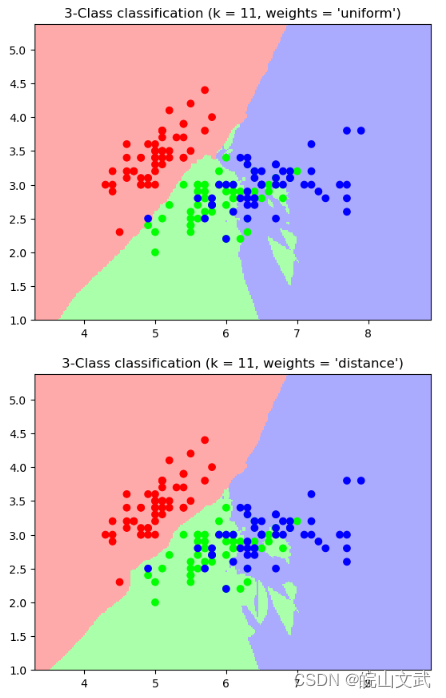
4. K值的确定

 KNN算法中只有一个超参数K，K值的确定对KNN算法的预测结果有着至关重要的影响。
 如果K值比较小，相当于在较小的领域内训练样本并对实例（预测样本）进行预测。这时，算法的近似误差会比较小，因为只有与实例相近的训练样本才会对预测结果起作用。但是，它也有明显的缺点：算法的估计误差比较大，预测结果会对邻近点十分敏感，如果邻近点是噪声点的话，预测就会出错。因此，K值过小容易导致KNN算法的过拟合。
 同理，如果K值选择较大的话，距离较远的训练样本也能够对实例预测结果产生影响。这时候，模型相对比较鲁棒，不会因为个别噪声对最终预测结果产生影响。但是缺点也十分明显：算法的邻近误差会偏大，距离较远的点（与预测实例不相似）也会同样对预测结果产生影响，使得预测结果产生较大偏差，此时模型容易发生欠拟合。
  在实际工程实践中，一般采用交叉验证的方式选取K值。通过以上分析可知，一般尽量在较小范围内选取K值，同时把测试集上准确率最高的那个K值确定为最终算法的参数K。