题目描述

给定你一个长度为 $n$ 的整数数列。

请你使用快速排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 $n$。

第二行包含 $n$ 个整数（所有整数均在 $1\sim 10^9$ 范围内），表示整个数列。

输出格式

输出共一行，包含 $n$ 个整数，表示排好序的数列。

数据范围

$1\le n\le 100000$

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

---

算法

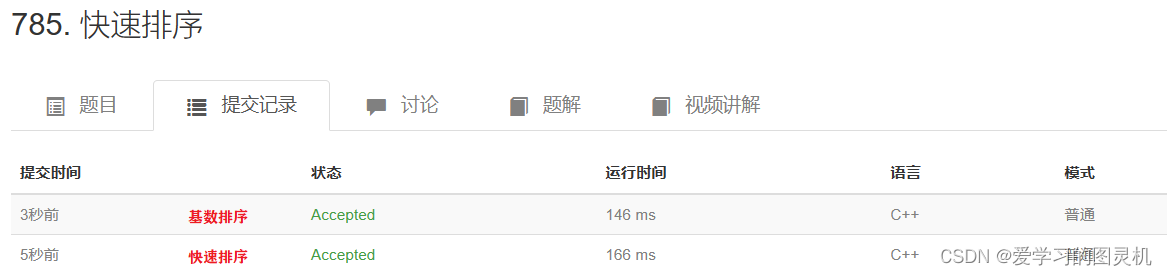
基数排序

网上搜索基数排序C++，大多都是非常低效的实现，于是自己动手实现一个速度较快的版本。

基数排序原理：一图胜千言

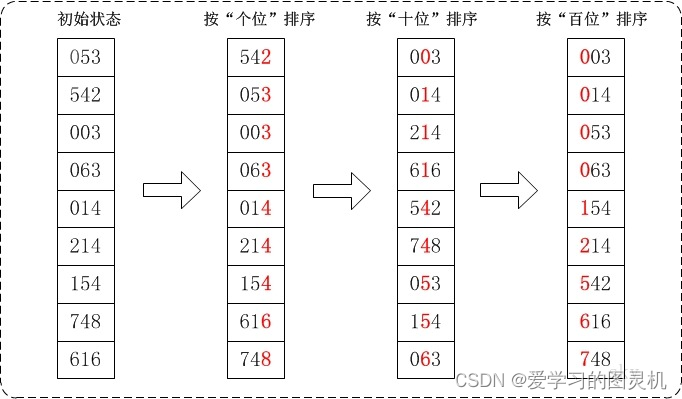
在$10$进制下，每次取个位和十位需要用除法和模运算，为了规避除法和模运算，采用$16$进制收集排序。实际测试比快速排序略快（数据量$1e5$较小，出到$1e7$差距会很大）。

---

时间复杂度 $\Theta (dn)$

最多扫描$d=lo{g}_{16}S$轮， S = max ⁡ { i ∈ [ 1 , N ] ∣ a [ i ] } S=\max\{i\in \left[ 1,N \right] \vert a[i]\} S=max{i∈[1,N]∣a[i]}，每轮收集$n$个元素，故 $\Theta (dn)$

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e5 + 10;
int a[N], n, k, ma, l = 16;
int buck[16][N];
int cnt[16];

void radix_sort(int k){
    int mod = 0;
    int t, c;
    for(int r = 0; r < k; ++ r){
        memset(cnt, 0, sizeof cnt);
        for(int i = 0; i < n; ++ i){
            t = (a[i] >> (mod * 4)) & 15;
            buck[t][cnt[t] ++ ] = a[i];
        }
        mod ++;
        for(int i = 0, c = 0; i < l; ++ i)
            for(int j = 0; j < cnt[i]; ++ j)
                a[c ++] = buck[i][j];
    }
    
}

int main(){
    scanf("%d", &n);
    for(int i = 0; i < n; ++ i){
        scanf("%d", &a[i]);
        ma = max(ma, a[i]);
    }
    
    while(ma > 0){
        ma /= l;
        k ++;
    }
    
    radix_sort(k);
    
    for(int i = 0; i < n; ++ i) printf("%d ", a[i]);
    
    
}