(直接截图比复制文字要好多了)
不会做的时候我去看了之前做的关于这道题目的笔记,
(Ak + 1)% k == 1 (Ak + 1 + Ak)% k == 1
只要发现了同余数的情况就说明有一个区间满足了题目的要求。
这个方法的精妙之处就在于前缀和包括了之前的前缀和和下一个的数字之和(相邻的两个是这样的,如此一来,单个数字 % k == 0的就也能够被检查到了,就是把单个数组也看作了是一个区间。准确说是结合才对。
(这里还是建议去多举几个例子,去理解一下这句话的含义))
不清楚问题,我直接去看了题解
顺着这个思路其实很容易就能发现一个方法——求出那些个区间再使用排列组合,把可能的组合都用公式计算出来。(考虑到一些区间是断裂的,由(Ak + 1)% k == 1 (Ak + 1 + Ak)% k == 1想到,一种特殊的可能就是区间里面的所有数字都可以被k整除) 但是转念一想,不是所有的数都一定是k的整数倍。但是受到Ak + 1)% k == 1 (Ak + 1 + Ak)% k == 1的影响,我还是只考虑了单个元素,而忘了区间的概念,区间的组合是可以用排列组合来处理的。于是我想到了下面的一一对比的方法。
package 练习;
import java.util.*;
public class K倍区间 {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt();
int K = scan.nextInt();
scan.nextLine();
int number = 0;
int[] sum = new int[N + 1];
for (int i = 1; i <= N; i++) {
sum[i] = scan.nextInt() + sum[i - 1];
for(int j = 0; j < i; j++)
if(sum[i] % K == sum[j] % K)
number ++;
scan.nextLine();
}
System.out.println(number);
}
}我想不明白,为什么我这for循环里面的for都似乎只有条件满足才执行的,为什么还是超时了。难道不管执不执行,两个for循环都会消耗大量的时间。
就是如此——
if语句本身的时间复杂度是O(1),即常数时间复杂度,不受问题规模N的影响。这是因为每次执行if语句时,仅进行一次条件判断,其执行时间是固定的,不随N的增大而增大。
时间复杂度能忽略掉if条件判断的情况是,其时间复杂度远远超过了if语句造成的影响。但是,如果if的执行次数是整个程序的大头就不能忽略了
事实上
每一条Java语句,或者任何编程语言中的语句,都有其执行所需的时间成本,可以理解为占有一定的“时间复杂度”。
找到占大头的开销语句,在没有积累起一些反例之前,不要被具体的例子蒙蔽了双眼,去考虑书上那些容易被忽略的知识。if 和 for循环里面的的都有可能让你的时间复杂度暴增。
回到问题本身,我们不难发现,这个if语句的时间复杂度为
N * (1 + 2 + 3 + ... + N)
= N * (N * (N + 1)) / 2
= O(N^3 / 2)
≈ O(N^3)这在蓝桥杯里面肯定是不可能被判定得分的。(除了数据特别少的情况下)
不成立的时候也总过有没有方法能和sum[ i ]的相同值,就像人脑一样,可以直接比较,看到了相同的数值就直接比较。但是计算机就是直接比较的,全部都要找一遍(for循环)但是又回到了原点。
最后我去看了题解,发现
#include<bits/stdc++.h>
using namespace std;
int n,k,a;
long long ans,sum,book[100005];
int main(){
cin >> n >> k;
book[0]++; //把S0放进去,因为S0=0,所以给book[0]++
for(int i=1;i<=n;i++){
scanf("%d",&a);
sum=(sum+a)%k; //sum是前缀和 也就是Si
book[sum]++;
}
for(int i=0;i<k;i++)//注意 余数是0~m-1
ans+=(book[i]*(book[i]-1))/2;
cout << ans;
return 0;
}
//by chenhaotian0219这里面的book[sum]吸引力我的注意。
这不就是映射吗,通过同余定理,把映射后的值域(0 < 数值 < k)设置数组也很方便,数值区间确定了,数组大小就不是问题了。(sun[ i ] % k == n == f (x) ),Y值域就是满足我们要求的,结合数组的特点就能够解决问题了。
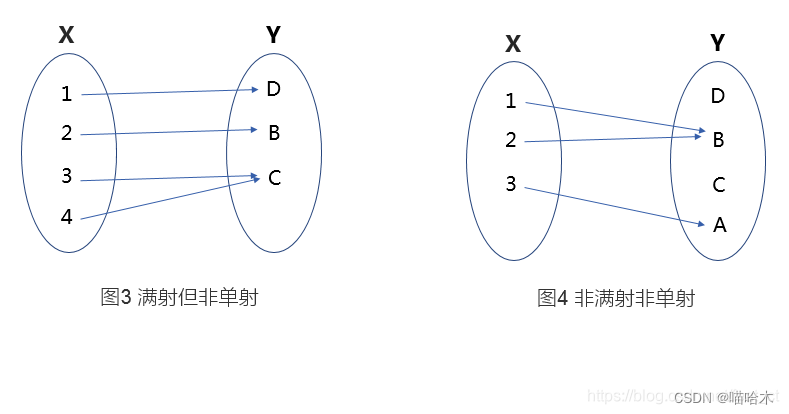
数据结构里面的散列表就是这样被设计的。
这样字直接比较就做到了,for循环只是为了然所有的sum[ i ]都显现出来。
也看到了
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a,sum,p[1000001],n,k,ans;
signed main(){
cin>>n>>k;
p[0]=1;//定义初始值
for(int i=1;i<=n;i++){
cin>>a;
sum+=a;
sum%=k;
p[sum]++;//对应余数的个数加一
}
for(int i=0;i<k;i++){
ans+=(p[i]*(p[i]-1)/2);//从n个数里面选两个,共有n*(n-1)/2种选法。
}
cout<<ans;
return 0;
}for(int i=0;i<k;i++){
ans+=(p[i]*(p[i]-1)/2);//从n个数里面选两个,共有n*(n-1)/2种选法。
}这格代码看起来很突兀,其实是我一开始的排列组合思考的排列组合,但是这里的是区间的。(最后这个for循环是从0开始的,指的是多格倍数部分,不是一个区间的)

单个区间的已经被计算过了(x),那么 a1 、 a2、a3 ... an 那么就是 n - 1 + n -2 + n - 3 + .. + 3 + 2 + 1(最后一个没有在里面,你把数字和个数一一对应就可以验证这个结论)。或者你这样子想——其实相互比较多是相邻的两个的sum[ i ]比较,组合就是跨国几个,还是两两比较。
一些无关的
签注和 —— 数列的和,如果你熟读数学,那么你可能就会独立发现这个算法。这就是数学的奥秘。